JavaSE基础06：递归函数（汉诺塔问题）

63 阅读 0 评论 42 点赞

我是靠谱客的博主无辜鸡，最近开发中收集的这篇文章主要介绍JavaSE基础06：递归函数（汉诺塔问题），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

在函数内部，可以调用其他函数。如果一个函数在内部调用自身本身，这个函数就是递归函数。举个例子，我们来计算阶乘n! = 1 x 2 x 3 x ... x n，用函数fact(n)表示，可以看出：

fact(n) = n! = 1 x 2 x 3 x ... x (n-1) x n = (n-1)! x n = fact(n-1) x n

所以，fact(n)可以表示为n x fact(n-1)，只有n=1时需要特殊处理。

于是，fact(n)用递归的方式写出来就是：

===> fact(5)
===> 5 * fact(4)
===> 5 * (4 * fact(3))
===> 5 * (4 * (3 * fact(2)))
===> 5 * (4 * (3 * (2 * fact(1))))
===> 5 * (4 * (3 * (2 * 1)))
===> 5 * (4 * (3 * 2))
===> 5 * (4 * 6)
===> 5 * 24
===> 120

递归函数的优点是定义简单，逻辑清晰。理论上，所有的递归函数都可以写成循环的方式，但循环的逻辑不如递归清晰。

使用递归函数需要注意防止栈溢出。在计算机中，函数调用是通过栈（stack）这种数据结构实现的，每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。由于栈的大小不是无限的，所以，递归调用的次数过多，会导致栈溢出。可以试试fact(1000)：

>>> fact(1000)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 4, in fact
  ...
  File "<stdin>", line 4, in fact
RuntimeError: maximum recursion depth exceeded

解决递归调用栈溢出的方法是通过尾递归优化，事实上尾递归和循环的效果是一样的，所以，把循环看成是一种特殊的尾递归函数也是可以的。

尾递归是指，在函数返回的时候，调用自身本身，并且，return语句不能包含表达式。这样，编译器或者解释器就可以把尾递归做优化，使递归本身无论调用多少次，都只占用一个栈帧，不会出现栈溢出的情况。

上面的fact(n)函数由于return n * fact(n - 1)引入了乘法表达式，所以就不是尾递归了。要改成尾递归方式，需要多一点代码，主要是要把每一步的乘积传入到递归函数中：

fact(n):
    return fact_iter(n, 1)

fact_iter(num, product):
    if num == 1:
        return product
    return fact_iter(num - 1, num * product)

斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368........这个数列从第3项开始，每一项都等于前两项之和。如果按照for循环来写则是这样的：

class Demon02{
  public static void main(String[] args){
       fibo(30);
    }
     
  public static void fibo(int n){
        int a=1;   //前两项为1
        int b=1;
        int c=0;   //存放第n项值
        for(int i=1;i<=n;i++){  
            if(i==1||i==2){  //如果i为1或者2 ，则值为1
                System.out.print(1+" ");
            }else{    //否则从第三项开始的第i项
                c=a+b;  //等于前两个值的和
                System.out.print(c+" ");  //记录每项的值
                a=b;   //将第i-1赋给a
                b=c;   //第i项赋给b
            }
        }
    }
}

如果用递归实现：

class Demon03{
   public static  void  main(String[] args){
        fibo_dg(30);
   }
 
 public static int fibo_dg(int n){
        if(n==1||n==2){  //如果是第1项或是第2项
            return 1;  //直接将结果返回1
        }
        return fibo_dg(n-1)+fibo_dg(n-2); //如果n>=3，就调用n-1项，直到n-1为2，将后两项相加得出结果返回
    }
}

使用递归函数的优点是逻辑简单清晰，缺点是过深的调用会导致栈溢出。

针对尾递归优化的语言可以通过尾递归防止栈溢出。尾递归事实上和循环是等价的，没有循环语句的编程语言只能通过尾递归实现循环。

汉诺塔问题

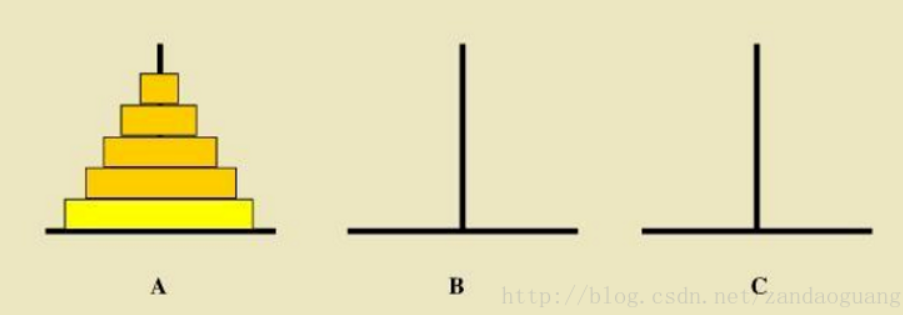
汉诺塔看似简单的几行代码，却蕴含着奇妙的算法。我从我个人学习的角度来说。我一开始理解了原理，但是编码不会编，这也就是所谓的眼高手低。多研究多在IDE（eclipse-java,VS-C/C++）调试，多看几遍，我想我们会一起进步！加油，为了自己的目标。
当只有一个盘子的时候，只需要从将A塔上的一个盘子移到C塔上。
当A塔上有两个盘子是，先将A塔上的1号盘子（编号从上到下）移动到B塔上，再将A塔上的2号盘子移动的C塔上，最后将B塔上的小盘子移动到C塔上。
当A塔上有3个盘子时，先将A塔上编号1至2的盘子（共2个）移动到B塔上（需借助C塔），然后将A塔上的3号最大的盘子移动到C塔，最后将B塔上的两个盘子借助A塔移动到C塔上。
当A塔上有n个盘子是，先将A塔上编号1至n-1的盘子（共n-1个）移动到B塔上（借助C塔），然后将A塔上最大的n号盘子移动到C塔上，最后将B塔上的n-1个盘子借助A塔移动到C塔上。
综上所述，除了只有一个盘子时不需要借助其他塔外，其余情况均一样（只是事件的复杂程度不一样）。
一、起源
汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

第一个为源；第二个为辅助盘，第三个为目标盘！

public class Hanoilmpl {


    public void hanoi(int n, char A, char B, char C) {
        if (n == 1) {
            move(A, C);
        } else {
            hanoi(n - 1, A, C, B);// 按ACB数序执行N-1的汉诺塔移动
            move(A, C);             //  执行最大盘子移动
            hanoi(n - 1, B, A, C);// 按BAC数序执行N-1的汉诺塔移动
        }
    }

    private void move(char A, char C) {//执行最大盘子的从A-C的移动
        System.out.println("move:" + A + "--->" + C);
    }

    public static void main(String[] args) {
        Hanoilmpl hanoi = new Hanoilmpl();
        System.out.println("移动汉诺塔的步骤：");
        hanoi.hanoi(3, 'a', 'b', 'c');
    }
}