环形队列是在实际编程极为有用的数据结构,它有如下特点。
它是一个首尾相连的FIFO的数据结构，采用数组的线性空间,数据组织简单。能很快知道队列是否满为空。能以很快速度的来存取数据。
因为有简单高效的原因，甚至在硬件都实现了环形队列.
环形队列广泛用于网络数据收发，和不同程序间数据交换（比如内核与应用程序大量交换数据,从硬件接收大量数据）均使用了环形队列.
一.环形队列实现原理
------------------------------------------------------------
内存上没有环形的结构，因此环形队列实上是数组的线性空间来实现。那当数据到了尾部如何处理呢？它将转回到0位置来处理。这个的转回是通过取模操作来执行的。
因此环列队列的是逻辑上将数组元素q[0]与q[MAXN-1]连接，形成一个存放队列的环形空间。
为了方便读写，还要用数组下标来指明队列的读写位置。head/tail.其中head指向可以读的位置，tail指向可以写的位置。
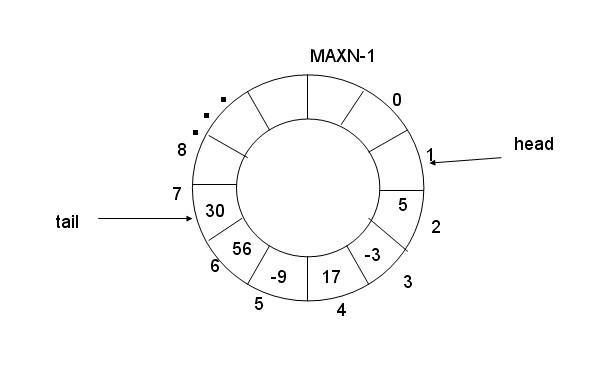
环形队列的关键是判断队列为空，还是为满。当tail追上head时，队列为满时，当head追上tail时，队列为空。但如何知道谁追上谁。还需要一些辅助的手段来判断.
如何判断环形队列为空，为满有两种判断方法。
一.是附加一个标志位tag
当head赶上tail，队列空，则令tag=0,
当tail赶上head，队列满，则令tag=1,
二.限制tail赶上head，即队尾结点与队首结点之间至少留有一个元素的空间。
队列空： head==tail
队列满： (tail+1)% MAXN ==head
二.附加标志实现算法
-------------------------------------------------------------
采用第一个环形队列有如下结构
1
2
3
4
5
6
7
8typedef struct ringq{ int head; /* 头部，出队列方向*/ int tail; /* 尾部，入队列方向*/ int tag ; int size ; /* 队列总尺寸 */ int space[RINGQ_MAX]; /* 队列空间 */ }RINGQ;
初始化状态: q->head = q->tail = q->tag = 0;
队列为空:( q->head == q->tail) && (q->tag == 0)
队列为满 : ((q->head == q->tail) && (q->tag == 1))
入队操作:如队列不满，则写入
q->tail = (q->tail + 1) % q->size ;
出队操作：如果队列不空，则从head处读出。
下一个可读的位置在 q->head = (q->head + 1) % q->size
完整代码
头文件ringq.h
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44#ifndef __RINGQ_H__ #define __RINGQ_H__ #ifdef __cplusplus extern "C" { #endif #define QUEUE_MAX 20 typedef struct ringq{ int head; /* 头部，出队列方向*/ int tail; /* 尾部，入队列方向*/ int tag ; /* 为空还是为满的标志位*/ int size ; /* 队列总尺寸 */ int space[QUEUE_MAX]; /* 队列空间 */ }RINGQ; /* 第一种设计方法: 当head == tail 时，tag = 0 为空，等于 = 1 为满。 */ extern int ringq_init(RINGQ * p_queue); extern int ringq_free(RINGQ * p_queue); /* 加入数据到队列 */ extern int ringq_push(RINGQ * p_queue,int data); /* 从队列取数据 */ extern int ringq_poll(RINGQ * p_queue,int *p_data); #define ringq_is_empty(q) ( (q->head == q->tail) && (q->tag == 0)) #define ringq_is_full(q) ( (q->head == q->tail) && (q->tag == 1)) #define print_ringq(q) printf("ring head %d,tail %d,tag %dn", q->head,q->tail,q->tag); #ifdef __cplusplus } #endif #endif /* __RINGQ_H__ */
实现代码 ringq.c
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66#include <stdio.h> #include "ringq.h" int ringq_init(RINGQ * p_queue) { p_queue->size = QUEUE_MAX ; p_queue->head = 0; p_queue->tail = 0; p_queue->tag = 0; return 0; } int ringq_free(RINGQ * p_queue) { return 0; } int ringq_push(RINGQ * p_queue,int data) { print_ringq(p_queue); if(ringq_is_full(p_queue)) { printf("ringq is fulln"); return -1; } p_queue->space[p_queue->tail] = data; p_queue->tail = (p_queue->tail + 1) % p_queue->size ; /* 这个时候一定队列满了*/ if(p_queue->tail == p_queue->head) { p_queue->tag = 1; } return p_queue->tag ; } int ringq_poll(RINGQ * p_queue,int * p_data) { print_ringq(p_queue); if(ringq_is_empty(p_queue)) { printf("ringq is emptyn"); return -1; } *p_data = p_queue->space[p_queue->head]; p_queue->head = (p_queue->head + 1) % p_queue->size ; /* 这个时候一定队列空了*/ if(p_queue->tail == p_queue->head) { p_queue->tag = 0; } return p_queue->tag ; }
测试代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87/* 测试第一种环形队列*/ void test5() { RINGQ rq, * p_queue; int i,data; p_queue = &rq; ringq_init(p_queue); for(i=0; i < QUEUE_MAX +2 ; i++) { ringq_push(p_queue,i+1); } if(ringq_poll(p_queue,&data)>=0) PRINT_INT(data); if(ringq_poll(p_queue,&data)>=0) PRINT_INT(data); if(ringq_poll(p_queue,&data)>=0) PRINT_INT(data); if(ringq_poll(p_queue,&data)>=0) PRINT_INT(data); if(ringq_poll(p_queue,&data)>=0) PRINT_INT(data); if(ringq_poll(p_queue,&data)>=0) PRINT_INT(data); ringq_free(p_queue); } /* 测试第一种环形队列,更加复杂的情况*/ void test6() { RINGQ rq, * p_queue; int i,data; p_queue = &rq; ringq_init(p_queue); ringq_push(p_queue,1); ringq_push(p_queue,2); if(ringq_poll(p_queue,&data)>=0) PRINT_INT(data); if(ringq_poll(p_queue,&data)>=0) PRINT_INT(data); if(ringq_poll(p_queue,&data)>=0) PRINT_INT(data); if(ringq_poll(p_queue,&data)>=0) PRINT_INT(data); ringq_push(p_queue,3); ringq_push(p_queue,4); ringq_push(p_queue,5); if(ringq_poll(p_queue,&data)>=0) PRINT_INT(data); if(ringq_poll(p_queue,&data)>=0) PRINT_INT(data); ringq_push(p_queue,6); if(ringq_poll(p_queue,&data)>=0) PRINT_INT(data); if(ringq_poll(p_queue,&data)>=0) PRINT_INT(data); ringq_free(p_queue); }
三.预留空间环境队列
-------------------------------------------------------------------
不采用tag,只留一个空间
初始化状态: q->head = q->tail = q->tag = 0;
队列为空:( q->head == q->tail)
队列为满 : (((q->tail+1)%q->size) == q->head )
入队操作:如队列不满，则写入
q->tail = (q->tail + 1) % q->size ;
出队操作：如果队列不空，则从head处读出。
下一个可读的位置在 q->head = (q->head + 1) % q->size
头文件
ringq.h
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42#ifndef __RINGQ_H__ #define __RINGQ_H__ #ifdef __cplusplus extern "C" { #endif #define RINGQ_MAX 20 typedef struct ringq{ int head; /* 头部，出队列方向*/ int tail; /* 尾部，入队列方向*/ int size ; /* 队列总尺寸 */ int space[RINGQ_MAX]; /* 队列空间 */ }RINGQ; /* 取消tag .限制读与写之间至少要留一个空间 队列空 head == tail . 队列满是 (tail+1)%MAX == head 初始化是head = tail = 0; */ extern int ringq_init(RINGQ * p_ringq); extern int ringq_free(RINGQ * p_ringq); extern int ringq_push(RINGQ * p_ringq,int data); extern int ringq_poll(RINGQ * p_ringq,int * p_data); #define ringq_is_empty(q) (q->head == q->tail) #define ringq_is_full(q) (((q->tail+1)%q->size) == q->head ) #define print_ringq2(q,d) printf("ring head %d,tail %d,data %dn", q->head,q->tail,d); #ifdef __cplusplus } #endif #endif /* __QUEUE_H__ */
实现代码ringq.c
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53#include <stdio.h> #include "ringq.h" int ringq_init(RINGQ * p_ringq) { p_ringq->size = RINGQ_MAX; p_ringq->head = 0; p_ringq->tail = 0; return p_ringq->size; } int ringq_free(RINGQ * p_ringq) { return 0; } /* 往队列加入数据 */ int ringq_push(RINGQ * p_ringq,int data) { print_ringq(p_ringq,data); if(ringq_is_full(p_ringq)) { printf("ringq is full,data %dn",data); return -1; } p_ringq->space[p_ringq->tail] = data; p_ringq->tail = (p_ringq->tail + 1) % p_ringq->size ; return p_ringq->tail ; } int ringq_poll(RINGQ * p_ringq,int * p_data) { print_ringq(p_ringq,-1); if(ringq_is_empty(p_ringq)) { printf("ringq is emptyn"); return -1; } *p_data = p_ringq->space[p_ringq->head]; p_ringq->head = (p_ringq->head + 1) % p_ringq->size ; return p_ringq->head; }
作者： Andrew Huang bluedrum@163.com
环形队列中实现队列的基本运算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62#include <iostream> #include <stdlib.h> #define MaxSize 10 using namespace std; typedef char ElemType; typedef struct { ElemType data[MaxSize]; int front,rear; } SqQueue; void InitQueue(SqQueue *q)//初始化队列InitQueue { //q=(SqQueue *)malloc(sizeof(SqQueue)); q->front=q->rear=0; } void DestroyQueue(SqQueue *q)//销毁队列DestroyQueue { free(q); } bool QueueEmpty(SqQueue *q)//判断队列是否为空QueueEmpty { return (q->front==q->rear); } bool enQueue(SqQueue *q,ElemType e)//进队列enQueue { if(<span style="color:#ffff66;background-color: rgb(255, 0, 0);">(q->rear+1)%MaxSize == q->front</span>) return false; else { <span style="color:#ffff66;">q->rear=(q->rear+1)%MaxSize;</span> q->data[q->rear]=e; return true; } } bool deQueue(SqQueue *q,ElemType &e)//出队列deQueue { if(q->front==q->rear) return false; else { <span style="background-color: rgb(255, 153, 0);">q->front=(q->front+1)%MaxSize;</span> e=q->data[q->front]; return true; } } int main() { SqQueue *q = new SqQueue(); char e; InitQueue(q); enQueue(q,'a'); cout<<QueueEmpty(q)<<endl; deQueue(q,e); cout<<e<<endl; DestroyQueue(q); cout<<QueueEmpty(q)<<endl; return 0; }
最后
以上就是粗犷鸡翅最近收集整理的关于【C/C++】环形队列实现原理环形队列中实现队列的基本运算的全部内容，更多相关【C/C++】环形队列实现原理环形队列中实现队列内容请搜索靠谱客的其他文章。
发表评论 取消回复