218. 天际线问题
2021.7.13 每日一题,以后再看
题目描述
城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度,请返回由这些建筑物形成的 天际线 。
每个建筑物的几何信息由数组 buildings 表示,其中三元组 buildings[i] = [lefti, righti, heighti] 表示:
lefti 是第 i 座建筑物左边缘的 x 坐标。
righti 是第 i 座建筑物右边缘的 x 坐标。
heighti 是第 i 座建筑物的高度。
天际线 应该表示为由 “关键点” 组成的列表,格式 [[x1,y1],[x2,y2],…] ,并按 x 坐标 进行 排序 。关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点,y 坐标始终为 0 ,仅用于标记天际线的终点。此外,任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。
注意:输出天际线中不得有连续的相同高度的水平线。例如 […[2 3], [4 5], [7 5], [11 5], [12 7]…] 是不正确的答案;三条高度为 5 的线应该在最终输出中合并为一个:[…[2 3], [4 5], [12 7], …]
示例 1:
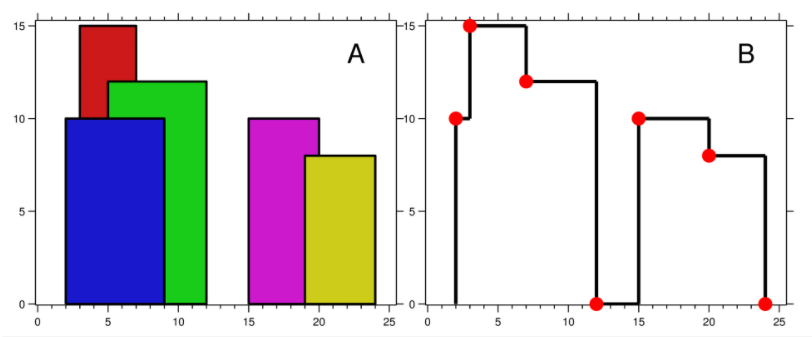
输入:buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
输出:[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
解释:
图 A 显示输入的所有建筑物的位置和高度,
图 B 显示由这些建筑物形成的天际线。图 B 中的红点表示输出列表中的关键点。
示例 2:
输入:buildings = [[0,2,3],[2,5,3]]
输出:[[0,3],[5,0]]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/the-skyline-problem
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
这道题有点难,说真的,不容易想明白
第一次做这种扫描线的题。
具体看代码吧,想法过程都写进去了
class Solution {
public List<List<Integer>> getSkyline(int[][] buildings) {
//又是一道前三百道的题,好好做一下
//首先排序,由左端点,然后记录最大右边缘
//然后遍历,先记录第一个点,然后找下一个左端点对应的高度,如果不同就输出左端点,同时更新最大右边缘
//然后判断当前右端点和下一个左端点的关系,如果左端点超过了最大右边缘那就是下一组了;
//如果在最大右边缘范围内,判读和上一个右端点的关系,如果小于,那么就是
//不行...
//看标签,树状数组,线段树...咋用呢。不是处理前后缀问题的吗
//看了一下官解,看了半天才看懂是干嘛,扫描线,就是从左到右扫描,看对应的点哪些是需要的点
//因为每个关键点都在左右边界上,且可以发现当关键点为某建筑的右边缘时,该建筑的高度对关键点的纵坐标是没有贡献的,这一点很重要
//先将每一个边缘都存入一个集合中,然后遍历这个集合,相当于从左到右扫描,
//找到在包含当前扫描线的区域内对应的最大高度,包含扫描线的区域就是一个建筑的[left,right)范围
//这样遍历需要n方的复杂度,为了优化复杂度,可以将最大高度存储到优先队列中
//然后根据右边界判断当前高度是否还满足条件,具体看代码吧
List<Integer> list = new ArrayList<>();
int l = buildings.length;
//将左右边界放到list中,相当于扫描线
for(int i = 0; i < l; i++){
list.add(buildings[i][0]);
list.add(buildings[i][1]);
}
//排序
Collections.sort(list);
//结果的集合
List<List<Integer>> res = new ArrayList<>();
//优先队列,存放高度和右边界,方便查找当前最大高度,按高度从大到小排序
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> (b[1] - a[1]));
//遍历所有扫描线
int idx = 0; //当前是第几个建筑物
for(int line : list){
//先看当前扫描线在哪几个建筑范围内
while(idx < l && buildings[idx][0] <= line){
//将右边缘和高度放入优先队列中,放右边缘是为了弹出
pq.offer(new int[]{buildings[idx][1], buildings[idx][2]});
idx++;
}
//如果当前队列头部的右边界小于等于当前扫描线,说明当前高度不可取,弹出
while(!pq.isEmpty() && line >= pq.peek()[0]){
pq.poll();
}
//到这里找到了当前扫描线对应的关键点
//取出最大高度,如果当前队列中没有点,说明是一组天际线的最右边位置,那么就是0
int height = pq.isEmpty() ? 0 : pq.peek()[1];
//如果当前扫描线对应的高度和上一个扫描线对应的高度相同,那么就跳过
if(res.isEmpty() || res.get(res.size() - 1).get(1) != height){
res.add(Arrays.asList(line, height));
}
}
return res;
}
}
看的另一种写法吧,先将扫描线和高度存储到优先队列中,这里有个很巧妙的操作,就是高度标记为负值的时候,说明是左端点,这个集合按照扫描线从小较大排列,高度从低到高(负数相当于从高到低)排列
然后将高度存储到TreeMap中,如果是左端点,就将高度放入集合中,如果是右端点,就删除当前高度,然后取出当前集合中的最大高度,就是当前扫描线对应的高度。为什么要用TreeMap而不是优先队列呢,因为在优先队列中找一个数删除,复杂度是O(n),TreeMap是对数复杂度
class Solution {
public List<List<Integer>> getSkyline(int[][] buildings) {
// x轴从小到大排序,如果x相等,则按照高度从低到高排序
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] != b[0] ? a[0] - b[0] : a[1] - b[1]);
for (int[] building : buildings) {
// 左端点和高度入队,高度为负值说明是左端点
pq.offer(new int[] { building[0], -building[2] });
// 右端点和高度入队
pq.offer(new int[] { building[1], building[2] });
}
List<List<Integer>> res = new ArrayList<>();
// 降序排列
TreeMap<Integer, Integer> heights = new TreeMap<>((a, b) -> b - a);
//放一个0,1。意思是,如果遍历到一组天际线的最右边,高度就是0
heights.put(0, 1);
int left = 0, height = 0;
while (!pq.isEmpty()) {
int[] arr = pq.poll();
// 如果是左端点
if (arr[1] < 0) {
// 高度 --> 高度 + 1
heights.put(-arr[1], heights.getOrDefault(-arr[1], 0) + 1);
}
// 右端点
else {
// 高度 --> 高度 - 1
heights.put(arr[1], heights.get(arr[1]) - 1);
// 说明左右端点都已经遍历完
if (heights.get(arr[1]) == 0) heights.remove(arr[1]);
}
// heights是以降序的方式排列的,所以以下会获得最大高度
int maxHeight = heights.keySet().iterator().next();
// 如果最大高度不变,则说明当前建筑高度在一个比它高的建筑下面,不做操作
if (maxHeight != height) {
left = arr[0];
height = maxHeight;
res.add(Arrays.asList(left, height));
}
}
return res;
}
}
粘贴一个三叶姐优先队列的
三叶姐那个图很直观的解释了这个题的意思,爱了
class Solution {
public List<List<Integer>> getSkyline(int[][] bs) {
List<List<Integer>> ans = new ArrayList<>();
// 预处理所有的点,为了方便排序,对于左端点,令高度为负;对于右端点令高度为正
List<int[]> ps = new ArrayList<>();
for (int[] b : bs) {
int l = b[0], r = b[1], h = b[2];
ps.add(new int[]{l, -h});
ps.add(new int[]{r, h});
}
// 先按照横坐标进行排序
// 如果横坐标相同,则按照左端点排序
// 如果相同的左/右端点,则按照高度进行排序
Collections.sort(ps, (a, b)->{
if (a[0] != b[0]) return a[0] - b[0];
return a[1] - b[1];
});
// 大根堆
PriorityQueue<Integer> q = new PriorityQueue<>((a,b)->b-a);
int prev = 0;
q.add(prev);
for (int[] p : ps) {
int point = p[0], height = p[1];
if (height < 0) {
// 如果是左端点,说明存在一条往右延伸的可记录的边,将高度存入优先队列
q.add(-height);
} else {
// 如果是右端点,说明这条边结束了,将当前高度从队列中移除
q.remove(height);
}
// 取出最高高度,如果当前不与前一矩形“上边”延展而来的那些边重合,则可以被记录
int cur = q.peek();
if (cur != prev) {
List<Integer> list = new ArrayList<>();
list.add(point);
list.add(cur);
ans.add(list);
prev = cur;
}
}
return ans;
}
}
作者:AC_OIer
链接:https://leetcode-cn.com/problems/the-skyline-problem/solution/gong-shui-san-xie-sao-miao-xian-suan-fa-0z6xc/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1818. 绝对差值和
2021.7.14每日一题
题目描述
给你两个正整数数组 nums1 和 nums2 ,数组的长度都是 n 。
数组 nums1 和 nums2 的 绝对差值和 定义为所有 |nums1[i] - nums2[i]|(0 <= i < n)的 总和(下标从 0 开始)。
你可以选用 nums1 中的 任意一个 元素来替换 nums1 中的 至多 一个元素,以 最小化 绝对差值和。
在替换数组 nums1 中最多一个元素 之后 ,返回最小绝对差值和。因为答案可能很大,所以需要对 109 + 7 取余 后返回。
|x| 定义为:
如果 x >= 0 ,值为 x ,或者
如果 x <= 0 ,值为 -x
示例 1:
输入:nums1 = [1,7,5], nums2 = [2,3,5]
输出:3
解释:有两种可能的最优方案:
- 将第二个元素替换为第一个元素:[1,7,5] => [1,1,5] ,或者
- 将第二个元素替换为第三个元素:[1,7,5] => [1,5,5]
两种方案的绝对差值和都是 |1-2| + (|1-3| 或者 |5-3|) + |5-5| = 3
示例 2:
输入:nums1 = [2,4,6,8,10], nums2 = [2,4,6,8,10]
输出:0
解释:nums1 和 nums2 相等,所以不用替换元素。绝对差值和为 0
示例 3:
输入:nums1 = [1,10,4,4,2,7], nums2 = [9,3,5,1,7,4]
输出:20
解释:将第一个元素替换为第二个元素:[1,10,4,4,2,7] => [10,10,4,4,2,7]
绝对差值和为 |10-9| + |10-3| + |4-5| + |4-1| + |2-7| + |7-4| = 20
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/minimum-absolute-sum-difference
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
非常典型的竞赛题,第三题
先想想暴力解,就是把第一个数组的所有数都用每一个数替换一遍,然后和第二个数组做差,看哪个小
时间复杂度是n方,超时
那么怎么优化呢
最直观会想到是不是把差的绝对值最大的项替换了,就能实现最后的和最小呢,想了一下,可以很简单举出反例
那么就继续想,对于nums2[i],nums1[i]替换成nums1中哪一项会使得结果最小呢,就是在nums1中找nums2[i]最接近的那一项。
然后就想到了,将nums1排序,然后在nums1中二分查找,找nums2[i]的插入位置
然后比较插入位置左右的数和当前数的差,进而找到最接近nums2[i]的数
找到了每个nums2[i]最接近的数,然后替换,看哪个替换前后绝对值差最大。最大的那个就是我们最后应该替换的
根据这个思路写的代码如下:
class Solution {
public static final int MOD = (int)1.0e9 + 7;
public int minAbsoluteSumDiff(int[] nums1, int[] nums2) {
//首先明确一点,对于每个位置,要替换,就是用nums1中最接近nums2[i]的数进行替换
//那么就想到在nums1中找nums2[i]的插入位置,然后附近的两个数就是和它最接近的数
//那么就把nums1排序然后二分查找
int l = nums1.length;
int[] temp = new int[l];
System.arraycopy(nums1, 0, temp, 0, l);
//排序
Arrays.sort(temp);
//找nums2[i]的插入位置
//这个哈希表存放nums[i]和nums1中哪个位置差值最小
Map<Integer, Integer> map = new HashMap<>();
for(int i = 0; i < l; i++){
int num = nums2[i];
if(map.containsKey(num))
continue;
int left = 0;
int right = l;
while(left < right){
int mid = (right - left) / 2 + left;
if(temp[mid] <= num){
left = mid + 1;
}else{
right = mid;
}
}
//此时找到的left就是插入的位置
//然后比较左右两边哪个和num接近
if(left == 0)
map.put(num, 0);
else if(left == l)
map.put(num, left - 1);
else if(Math.abs(num - temp[left - 1]) < Math.abs(num - temp[left]))
map.put(num, left - 1);
else
map.put(num, left);
}
//替换,看哪个替换最小,也就是找改变最大的
int change = 0;
int index = -1;
int diff = 0;
for(int i = 0; i < l; i++){
int idx = map.get(nums2[i]);
//原来差距
int differ1 = Math.abs(nums1[i] - nums2[i]);
//改变后的差距
int differ2 = Math.abs(temp[idx] - nums2[i]);
//如果改变最大,那么存储下来
if(differ1 - differ2 > change){
change = differ1 - differ2;
index = i;
diff = differ2;
}
}
int res = 0;
for(int i = 0; i < l; i++){
if(i == index){
res = (res + diff) % MOD;
}else
res = (res + Math.abs(nums1[i] - nums2[i])) % MOD;
}
return res;
}
}
我的代码太长了,优雅的代码
class Solution {
int mod = (int)1e9+7;
public int minAbsoluteSumDiff(int[] nums1, int[] nums2) {
int n = nums1.length;
int[] sorted = nums1.clone();
Arrays.sort(sorted);
long sum = 0, max = 0;
for (int i = 0; i < n; i++) {
int a = nums1[i], b = nums2[i];
if (a == b) continue;
int x = Math.abs(a - b);
sum += x;
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (sorted[mid] <= b) l = mid;
else r = mid - 1;
}
int nd = Math.abs(sorted[r] - b);
if (r + 1 < n) nd = Math.min(nd, Math.abs(sorted[r + 1] - b));
if (nd < x) max = Math.max(max, x - nd);
}
return (int)((sum - max) % mod);
}
}
作者:AC_OIer
链接:https://leetcode-cn.com/problems/minimum-absolute-sum-difference/solution/gong-shui-san-xie-tong-guo-er-fen-zhao-z-vrmq/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1846. 减小和重新排列数组后的最大元素
2021.7.15 每日一题
题目描述
给你一个正整数数组 arr 。请你对 arr 执行一些操作(也可以不进行任何操作),使得数组满足以下条件:
arr 中 第一个 元素必须为 1 。
任意相邻两个元素的差的绝对值 小于等于 1 ,也就是说,对于任意的 1 <= i < arr.length (数组下标从 0 开始),都满足 abs(arr[i] - arr[i - 1]) <= 1 。abs(x) 为 x 的绝对值。
你可以执行以下 2 种操作任意次:
减小 arr 中任意元素的值,使其变为一个 更小的正整数 。
重新排列 arr 中的元素,你可以以任意顺序重新排列。
请你返回执行以上操作后,在满足前文所述的条件下,arr 中可能的 最大值 。
示例 1:
输入:arr = [2,2,1,2,1]
输出:2
解释:
我们可以重新排列 arr 得到 [1,2,2,2,1] ,该数组满足所有条件。
arr 中最大元素为 2 。
示例 2:
输入:arr = [100,1,1000]
输出:3
解释:
一个可行的方案如下:
- 重新排列 arr 得到 [1,100,1000] 。
- 将第二个元素减小为 2 。
- 将第三个元素减小为 3 。
现在 arr = [1,2,3] ,满足所有条件。
arr 中最大元素为 3 。
示例 3:
输入:arr = [1,2,3,4,5]
输出:5
解释:数组已经满足所有条件,最大元素为 5 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-element-after-decreasing-and-rearranging
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
竞赛第二题吧最多算个哈哈
class Solution {
public int maximumElementAfterDecrementingAndRearranging(int[] arr) {
//先排序,然后将arr每个位置的最大值计算出来
//然后从左到右遍历,如果该位置小于最大值,那么后面的最大值也应该跟着更改
//如果大于最大值,那么就减小到最大值
int l = arr.length;
Arrays.sort(arr);
int first = 1;
for(int i = 1; i < l; i++){
if(arr[i] >= first + 1){
first++;
}else{
first = arr[i];
}
}
return first;
}
}
早上起来看到的官解思路,挺巧妙的
class Solution {
public int maximumElementAfterDecrementingAndRearranging(int[] arr) {
//昨晚没有官解,今天看到官解计数排序的方法,还是很巧妙的
int l = arr.length;
//记录每个数字出现的个数,大于l的就存放在最后一个位置,因为它能补充任何数
int[] count = new int[l];
for(int n : arr){
count[Math.min(l, n) - 1]++;
}
//缺失的个数
int miss = 0;
for(int i = 0; i < l; i++){
//如果没有这个值,那么缺失个数加一
if(count[i] == 0){
miss++;
//如果有这个值,那么填充缺失
}else{
miss -= Math.min(miss, count[i] - 1);
}
}
return l - miss;
}
}
最后
以上就是深情书本最近收集整理的关于LeetCode 218. 天际线问题(扫描线)/ 1818. 绝对差值和/ 1846. 减小和重新排列数组后的最大元素218. 天际线问题1818. 绝对差值和1846. 减小和重新排列数组后的最大元素的全部内容,更多相关LeetCode内容请搜索靠谱客的其他文章。



![D - Snuke Panic (1D)(DP)[ AtCoder Beginner Contest 266]题目如下:思路 or 题解:AC代码如下:](https://www.shuijiaxian.com/files_image/reation/bcimg8.png)




发表评论 取消回复