1. 首页
  2. 文章中心
  3. 数据结构与算法

AGC005 补题小结

59 阅读 0 评论
我是靠谱客的博主 落后黑裤，最近开发中收集的这篇文章主要介绍AGC005 补题小结，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Problem A STring

简要题意：有一个字符串 (X) ，对它进行操作。 该串只含字符 ('S') 和 ('T') ，凡是 ('S') 与 ('T') 连在一起都要将它们一起去掉 现在进行若干次操作直到该串中没有连在一起的 ('ST') ，问剩下的长度。 (|X|le 2times 10^5)

tag：模拟

题解：两个指针扫一遍即可

#include <cstdio>
#include <cstring>
const int N=200005;
char a[N],b[N];
int main (){
    scanf ("%s",b+1);
    int n=strlen(b+1),m=0,ans=n;
    for (int i=1;i<=n;i++){
        if (a[m]=='S'&&b[i]=='T') ans-=2,--m;
        else a[++m]=b[i];
    }
    printf ("%d",ans);
    return 0;
}

Problem B Minimum Sum

简要题意：给定一个长度为 (n) 的数组 (a) ，满足 (a) 是 (1...n) 的一个排列，求 (sum_{i=1}^nsum_{j=i}^nMin(a[l]...a[r])) (nle 2times 10^5)

tag：模拟，单调栈

题解：记 (l[i],r[i]) 表示 (a[i]) 是 (a[l[i]]...a[r[i]]) 中的最小值，也就是最左和最右能到的地方，这个东西可以使用单调栈维护

#include <cstdio>
const int N=200005;
int a[N];long long ans=0;
int l[N],r[N],s[N],pos[N],top=0;
int main (){
    int n;scanf ("%d",&n);
    for (int i=1;i<=n;i++) scanf ("%d",&a[i]);
    s[top=1]=0,pos[top]=0;
    for (int i=1;i<=n;i++){
        while (top>0&&s[top]>a[i]) --top;
        l[i]=pos[top]+1;s[++top]=a[i],pos[top]=i;
    }
    s[top=1]=0,pos[top]=n+1;
    for (int i=n;i>=1;i--){
        while (top>0&&s[top]>a[i]) --top;
        r[i]=pos[top]-1;s[++top]=a[i],pos[top]=i;
    }
    for (int i=1;i<=n;i++)
        ans+=1ll*(r[i]-i+1)*(i-l[i]+1)*a[i];
    printf ("%lld",ans);
    return 0;
}

Problem C Tree Restoring

简要题意：给定一个数列 (a_i) ，要构造一棵树，使得其边权为 (1) ，并且距离点 (i) 最远的点离它的距离是 (a_i) ，只要输出能否构成即可。 (nle 100)

tag：分类讨论，构造

题解：树上一个点的最远点，一定是直径两个端点之一，所以我们先找出直径的长度 (L) ，然后分类讨论

  • (L) 是偶数，那么 (a_i=frac{L}{2}) 的只有一个，满足 $ frac{L}{2} < a_i < L$ 的任意 (a_i) 至少有两个，不能存在 (< frac{L}{2}) 的
  • (L) 是奇数，那么 (a_i=frac{L+1}{2}) 的只能有两个，满足 (frac{L+1}{2} < a_i < L) 的任意 (a_i) 至少有两个，不能存在 (< frac{L+1}{2}) 的
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define gg return 0
const int N=105;
int a[N],b[N];
int main (){
    int n,L=0;scanf ("%d",&n);
    for (int i=1;i<=n;i++) scanf ("%d",&a[i]),L=max(L,a[i]),b[a[i]]++;
    if (L&1){
        int l=(L+1)/2;
        for (int i=1;i<l;i++) if (b[i]) {puts("Impossible");gg;}
        if (b[l]!=2) {puts("Impossible");gg;}
        for (int i=l+1;i<=L;i++) if (b[i]<2) {puts("Impossible");gg;} 
    }else{
        int l=L/2;
        for (int i=1;i<l;i++) if (b[i]) {puts("Impossible");gg;}
        if (b[l]!=1) {puts("Impossible");gg;}
        for (int i=l+1;i<=L;i++) if (b[i]<2) {puts("Impossible");gg;}
    }
    puts("Possible");
    return 0;
}

Problem D ~K Perm Counting

简要题意：给定数字 (n,k) ，求有多少 (1...n) 的排列 (P) 满足 (forall _i|i-P_i| not= k) ，对质数 (924844033) 取模 (nle 2000)

tag：组合数学，dp，思维

题解：考虑容斥，设 (f(i)) 表示至少有 (i) 个位置不满足的方案数，显然答案等于 (sum_{i=0}^{n} (-1)^itimes f(i) times (n-i)!)

考虑把每个位置和每个值看作一个点，差为 (k) 的之间连边，这样我们获得了一个点数为 (2times n) 的二分图。

问题变成了选择 (i) 条边的方案数。

化成图大概是这样

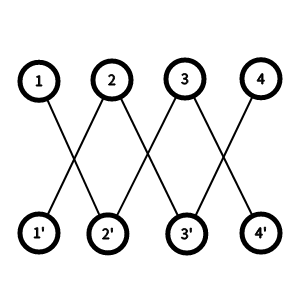
1428579-20181221195944073-571497050.png

然后通过观察可以发现，整个二分图其实可以拆出来恰好 (2times k) 条链，那么对这 (2times k) 条链进行 dp 即可

在每一条链上，设 (g[i][j][0/1]) 表示前 (i) 个点，已经出现了 (j) 对冲突，(i,i+1) 之间是否连通的方案数

转移非常简单 (g[i][j][0]=g[i-1][j][0]+g[i-1][j][1]) (g[i][j][1]=g[i-1][j-1][0])

最后统计答案：(f[i]=g[end][i][0]+g[end][i][1]) ，统计答案可以使用背包，但是也有一个很巧妙的做法：把 (2times k) 条链连起来，只要在结尾出不转移第二个方程即可。

#include <cstdio>
const int Mod=924844033,N=2005;
int g[N<<1][N][2];bool end[N<<1];
int fac[N<<1];
inline int mo(int x){return x<Mod?x:x%Mod;}
int main (){
    int n,k;scanf ("%d%d",&n,&k);fac[0]=1;
    for (int i=1;i<=(n<<1);i++) fac[i]=1ll*fac[i-1]*i%Mod;
    for (int i=1,now=0;i<=k;i++){
        int d=(n-i)/k+1;
        end[now+=d]=true,end[now+=d]=true;
    }
    g[1][0][0]=1;
    for (int i=1;i<=(n<<1);i++)
        for (int j=0;j<=n;j++){
            g[i+1][j][0]=mo(g[i][j][0]+g[i][j][1]);
            if (!end[i]) g[i+1][j+1][1]=g[i][j][0];
        }
    int ans=0;
    for (int i=0;i<=n;i++){
        int now=1ll*fac[n-i]*(g[n+n][i][0]+g[n+n][i][1])%Mod;
        if (i&1) ans=mo(ans-now+Mod);
        else ans=mo(ans+now);
    }
    printf ("%d",ans);
    return 0;
}

Problem E Sugigma: The Showdown

简要题意：两个人玩游戏，(A,B) 各有一棵节点数为 (n) 的树，(A) 在树 (a) 上的点 (x) ，(B) 在树 (b) 上的点 (y) ，在奇数轮，(A) 可以走到一个相邻节点或原地不动，类似的，偶数轮 (B) 可以走到一个相邻节点或原地不动，当两人到了编号相同的点游戏结束，(A) 希望能玩尽可能久，(B) 希望尽快结束，两人足够聪明，求轮数，无限轮输出 (-1) (nle 2times 10^5)

tag：博弈，讨论，贪心

题解：若有红树上有一条边，它的两个端点在蓝树上的距离大于 (2) ，则如果先手到达了这两个端点，就必胜。

建出蓝树，以后手起点为根，算出所有点深度。

然后建出红树，删掉满足以上条件的边（也就是建的时候就不加），然后看先手能到那些点。

由于红树上任意一条边连接的两点在蓝树上的距离小于等于 (2) ，所以如果一个点到先手起点的距离大于等于到后手起点的距离，先手走这点就一定会被后手抓，所以不能走。这样如果它能到必胜点，就输出 (-1) ，否则选择在蓝树上深度最大的那个点，然后弃疗等死。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N=200005;
int deep[N],dfn[N],ed[N],fa[N],dis[N],Time,ans;
struct Tree{
    int Head[N],Next[N<<1],Adj[N<<1],tot;
    inline void addedge(int u,int v){
        Next[++tot]=Head[u],Head[u]=tot,Adj[tot]=v;
        Next[++tot]=Head[v],Head[v]=tot,Adj[tot]=u;
    }
    inline void dfs(int x,int f){
        dfn[x]=++Time,fa[x]=f;
        for (int e=Head[x];e;e=Next[e])
            if (Adj[e]!=f){
                dis[Adj[e]]=dis[x]+1;
                dfs(Adj[e],x);
            }
        ed[x]=Time;
    }
    inline bool check(int x,int y){
        if (dfn[x]>dfn[y]) swap(x,y);
        if (dfn[y]>=dfn[x]&&dfn[y]<=ed[x]) return dis[y]-dis[x]>2;
        return fa[x]!=fa[y];
    }
    inline void dfs2(int x,int f){
        if (deep[x]>=dis[x]) return;
        ans=max(ans,dis[x]*2);
        for (int e=Head[x];e;e=Next[e])
            if (Adj[e]!=f){
                deep[Adj[e]]=deep[x]+1;
                dfs2(Adj[e],x);
                if (check(x,Adj[e])) {puts("-1");exit(0);}
            }
    }
}T1,T2;
int main(){
    int n,x,y;scanf ("%d%d%d",&n,&x,&y);
    if (x==y){puts("0");return 0;}
    for (int i=1;i<n;i++){
        int u,v;scanf ("%d%d",&u,&v);
        T1.addedge(u,v);
    }
    for (int i=1;i<n;i++){
        int u,v;scanf ("%d%d",&u,&v);
        T2.addedge(u,v);
    }
    T2.dfs(y,0);
    T1.dfs2(x,0);
    printf ("%d",ans);
    return 0;
}

Problem F Many Easy Problems

简要题意：给定一棵 (n) 个节点的无根树，定义 (g(i)) 表示对于所有大小为 (i) 的点集，包含它们的最小连通块大小之和，对于 (1le i le n) 输出 (g(i)) 答案对 (924844033) 取模。(nle 2times 10^5) (924844033 =2^{21}*3^2*7^2+1)

tag：容斥，(dp)，​(NTT)

题解：

设 (f(s)) 表示点集 (s) 的方案数，那么 (g(k)) 就是 (binom{n}{k}) 个 (f) 值之和

直接计算 (f(s)) 是一个很困难的事情，所以换一个角度，考虑每个点对于答案的贡献。

发现一个点 (x) 对当前的选择方案没有贡献当且仅当选择的 (k) 个点都在 (x) 的某个儿子的子树中，然后总的方案数就是 (binom{n}{k})

所以可以容斥求出一个点在选择 (k) 个点时候的答案 ，式子长这样：
[ val_k(x)=binom{n}{i}-sum_{uin son(x)} binom{size[u]}{k} ]
所以可以推出最终答案
[ f(k)=sum_{i=1}^nval_k(i)=ntimes binom{n}{i}-sum_{i=1}^nsum_{uin son(i)} binom{size[u]}{k} ]
我们把相同的 (size) 合并一下，记 (cnt[i]) 表示 (size=i) 的节点数
[ f(k)=ntimes binom{n}{i}-sum_{i=k}^n cnt[i]times binom{i}{k} ]
这个式子直接计算的复杂度过高，不能承受，考虑变形一下

前面的 (ntimes binom{n}{i}) 可以单独计算，所以考虑后面部分
[ begin{aligned} f'(k)&=sum_{i=k}^n cnt[i]times binom{i}{k}\ &=sum_{i=k}^ncnt[i]times frac{i!}{k!times (i-k)!}\ end{aligned} ]
因为 (k) 是常数，所以可以把 (k!) 拉出来
[ f'(k)times =frac{1}{k!}sum_{i=k}^n cnt[i]times i!times frac{1}{(i-k)!} ]
设 (A[i]=cnt[i]times i!)，(B[i]=frac{1}{i!}) 翻转 (B) 构造卷积形式 (B[n-i]=frac{1}{i!})

那么 (f'(k)=frac{1}{k!}sum_{i+j=k+n}A[i]B[j])

(NTT) 即可,答案中指数为 (n+k) 的项的系数就是 (f'(k))，时间复杂度 (O(nlogn)) 。

注意模数 (924844033 =2^{21}*3^2*7^2+1) 的原根是 (5)

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int Mod=924844033,g=5,gi=554906420;
const int N=200005;
inline int qpow(int a,int b){
    int ans=1;
    while (b){
        if (b&1) ans=1ll*ans*a%Mod;
        a=1ll*a*a%Mod,b>>=1;
    }
    return ans;
}
int rev[N<<2],a[N<<2],b[N<<2],lim;
inline void NTT_init(int n){
    int l=0;for (lim=1;lim<=(n<<1);lim<<=1) ++l;
    for (int i=1;i<=lim;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
}
inline void NTT(int*s,int t){
    for (int i=0;i<lim;i++) if (i<rev[i]) swap(s[i],s[rev[i]]);
    for (int mid=1;mid<lim;mid<<=1){
        int wn=qpow(t==1?g:gi,(Mod-1)/(mid<<1));
        for (int i=0;i<lim;i+=(mid<<1)){
            int w=1;
            for (int j=0;j<mid;j++,w=1ll*w*wn%Mod){
                int x=s[i+j],y=1ll*s[i+j+mid]*w%Mod;
                s[i+j]=(x+y)%Mod,s[i+j+mid]=(x-y+Mod)%Mod;
            }
        }
    }
    if (t==-1) {
        int inv=qpow(lim,Mod-2);
        for (int i=0;i<=lim;i++) s[i]=1ll*s[i]*inv%Mod;
    }
}
int size[N],cnt[N],fac[N],fac_inv[N];
int n;
inline void binom_init(){
    fac[0]=1;
    for (int i=1;i<=n;i++) fac[i]=1ll*fac[i-1]*i%Mod;
    fac_inv[n]=qpow(fac[n],Mod-2);
    for (int i=n-1;i>=0;i--) fac_inv[i]=1ll*fac_inv[i+1]*(i+1)%Mod; 
}
inline int C(int x,int y){
    return 1ll*fac[x]*fac_inv[y]%Mod*fac_inv[x-y]%Mod;
}
int Head[N],Next[N<<1],Adj[N<<1],tot=0;
inline void addedge(int u,int v){
    Next[++tot]=Head[u];
    Head[u]=tot;
    Adj[tot]=v;
    Next[++tot]=Head[v];
    Head[v]=tot;
    Adj[tot]=u;
}
inline void dfs(int x,int f){
    size[x]=1;
    for (int e=Head[x];e;e=Next[e])
        if (Adj[e]!=f){
            dfs(Adj[e],x);
            size[x]+=size[Adj[e]];
        }
    if (f) cnt[size[x]]++,cnt[n-size[x]]++;
}
int f[N];
int main (){
    scanf ("%d",&n);
    for (int i=1,u,v;i<n;i++){
        scanf ("%d%d",&u,&v);
        addedge(u,v);
    }
    dfs(1,0);
    binom_init();
    NTT_init(n);
    for (int i=1;i<=n;i++) a[i]=1ll*cnt[i]*fac[i]%Mod;
    for (int i=0;i<=n;i++) b[n-i]=fac_inv[i];
    NTT(a,1),NTT(b,1);
    for (int i=0;i<=lim;i++) a[i]=1ll*a[i]*b[i]%Mod;
    NTT(a,-1);
    for (int i=1;i<=n;i++) f[i]=1ll*a[n+i]*fac_inv[i]%Mod;
    for (int i=1;i<=n;i++) printf ("%dn",(1ll*n*C(n,i)%Mod-f[i]+Mod)%Mod);
    return 0;
}

转载于:https://www.cnblogs.com/crazyzh/p/10883762.html

最后

以上就是落后黑裤为你收集整理的AGC005 补题小结的全部内容，希望文章能够帮你解决AGC005 补题小结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(39)

相关文章

agc016D - XOR Replace(图论 智商)
agc016D - XOR Replace(图论 智商)
Atcoder Grand Contest 016 D XOR Replace
Atcoder Grand Contest 016 D XOR Replace
【题解】AtCoder Grand Contest 016
【题解】AtCoder Grand Contest 016
[agc016F] Games on DAG
[agc016F] Games on DAG
AGC005 补题小结
AGC005 补题小结
AGC016 A - Shrinking（暴力）
AGC016 A - Shrinking（暴力）
leetcode1015 至少有1位重复的数字
leetcode1015 至少有1位重复的数字
【AGC016F】Games on DAG（SG函数，状压DP，子集枚举）
【AGC016F】Games on DAG（SG函数，状压DP，子集枚举）

评论列表共有 0 条评论

立即
投稿
返回
顶部