AGC010 - D: Decrementing

分析

这是一道和奇偶性有关的题目。
很容易知道拿到$1,1,1,...,1$就输了，此时手里数的和$sum$等于$n$。

考虑$sum$奇偶性的转换关系。

或者再展开一点：

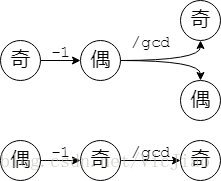
偶-奇 是必然的很好理解，重点考虑一下$sum$为奇数的情形。
奇(-偶)-奇 要求gcd为偶数，因为偶/奇=偶。因此原数列%2必然是000…01的形式，而我可以将其变为000…11从而形成奇-偶 。所以奇-奇 是一定条件下可选的，奇-偶 是任何条件下可行的。

由此再考虑$n$的奇偶性对答案的影响。

1. $n$为偶数
   能保持$sum$为奇数的一方一定不会输。既然$sum$一直是奇数，那么就一定不会得到$1,1,1,...,1$的状态，必胜。而因为拿到奇数的一方一定可以给对手一个偶数，而对手只能无可奈何地还你一个奇数。所以初始$sum$为奇数则先手必胜，否则必败。
   时间复杂度为$O(n)$。

   • $n$为奇数
     能保持$sum$为偶数的一方一定不会输。但是拿到偶数的一方需要保证对手不会还回来一个奇数，下面证明这一点一定可以做到。

     证明

     首先奇数方要是想还给对手一个奇数必然要使gcd不为1，所以原数列%gcd必然是000…01的形式。再考虑这个状态是怎么达到的：
     
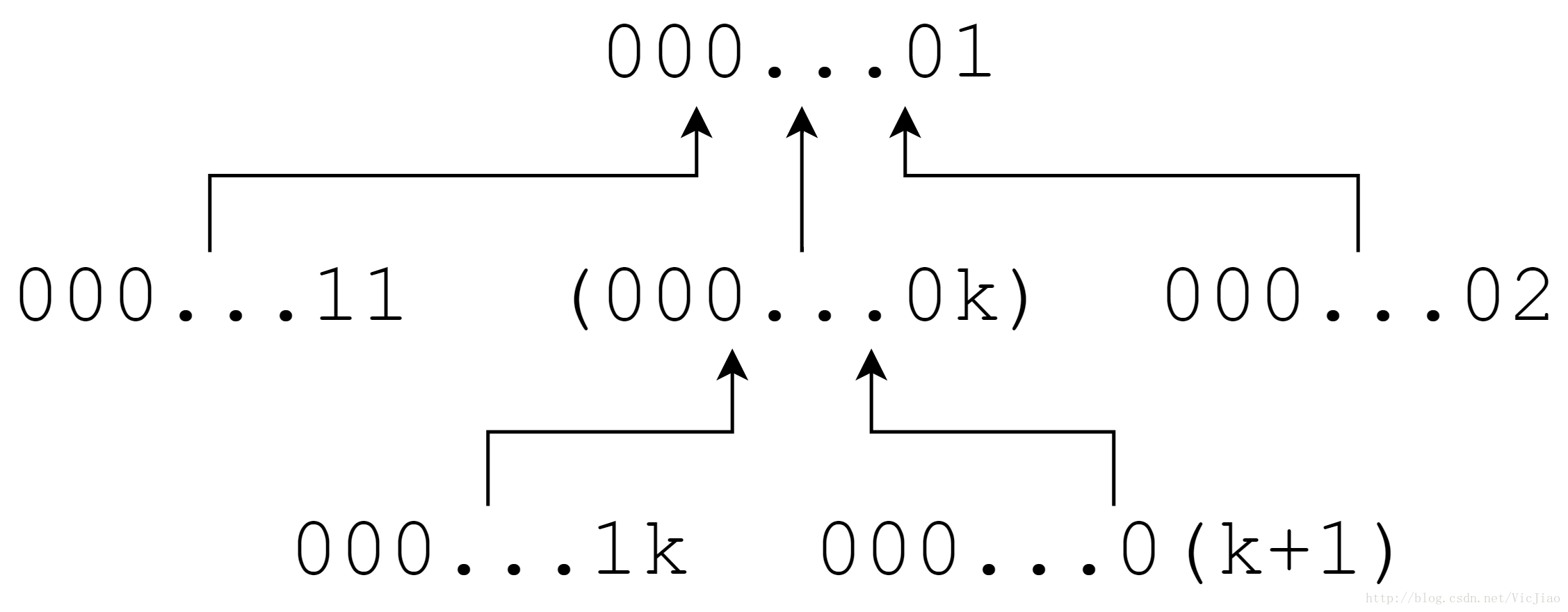
     对于000…11，000…02，000…1k，000…0(k+1)这四种状态另一方都有办法规避000…01的结果。所以拿到偶数的一方一定能保证下一轮自己还是偶数。

     因此初始$sum$为偶数的话先手必胜。
     时间复杂度为$O(n)$。

     但是初始$sum$是奇数并不意味着必败；因为此时还没有另一方的干扰，是有可能给对手一个奇数的。但是由于你可能只有极少的选择方案，这给了对手可乘之机：对手也有可能还回来一个奇数。以此循环往复，无法给对手奇数的一方会输掉游戏。
     因为每次都会给所有数除以一个大于1的gcd，所以最多往复$log_{2}({min{a})}$次，其中每次操作的复杂度是$O(n)$。时间复杂度最大为$O(ncdot log_{2}({min{a}}))$。

   • 总时间复杂度最大为$O(ncdot log_{2}({min{a}}))$。

     实现

     只有$n$，$sum$均为奇数时无法通过判断$n$和$sum$的奇偶性来得出答案。
     计算出前缀gcd$g_1$和后缀gcd$g_2$，然后计算$gcd{g_1[i-1],a[i]-1,g_2[i+1]}$，如果 $(sum-1)/gcd$ 为奇数就令所有数除以gcd，然后轮到对手。若没有可能的gcd，GG。

     代码

     //Decrementing
     #include <cstdio>
     typedef long long lint;
     int const N=1e5+10;
     int n,a[N];
     int gcd(int x,int y)
     {
         if(x==-1 || y==-1) return -x*y;
         if(x==0) return y;
         else return gcd(y%x,x);
     }
     int g1[N],g2[N];
     int main()
     {
         scanf("%d",&n);
         lint sum=0;
         for(int i=1;i<=n;i++) scanf("%d",&a[i]),sum+=a[i];
         if(n%2==0)
         {
             if(sum%2==1) printf("First");
             else printf("Second");
             return 0;
         }
         if(sum%2==0) {printf("First"); return 0;}
         int cur=0;
         while(true)
         {
             bool flag=false;
             sum=0;
             for(int i=1;i<=n;i++) sum+=a[i];
             g1[0]=-1; g2[n+1]=-1;
             for(int i=2;i<=n;i++) g1[i]=gcd(g1[i-1],a[i]);
             for(int i=n-1;i>=1;i--) g2[i]=gcd(g2[i+1],a[i]);
             int g;
             for(int i=1;i<=n&&!flag;i++)
             {
                 if(a[i]==1) continue;
                 g=gcd(gcd(g1[i-1],g2[i+1]),a[i]-1);
                 if(((sum-1)/g)%2==1) flag=true;
             }
             if(flag)
                 for(int i=1;i<=n;i++) a[i]/=g;
             else
             { 
                 if(cur==0) printf("Second");
                 else printf("First");
                 return 0; 
             } 
             cur^=1;
         }
         return 0;
     }

     注意

     挺好写的，主要是思维难度高