AGC010 B - Boxes（思维，数学）

题意：

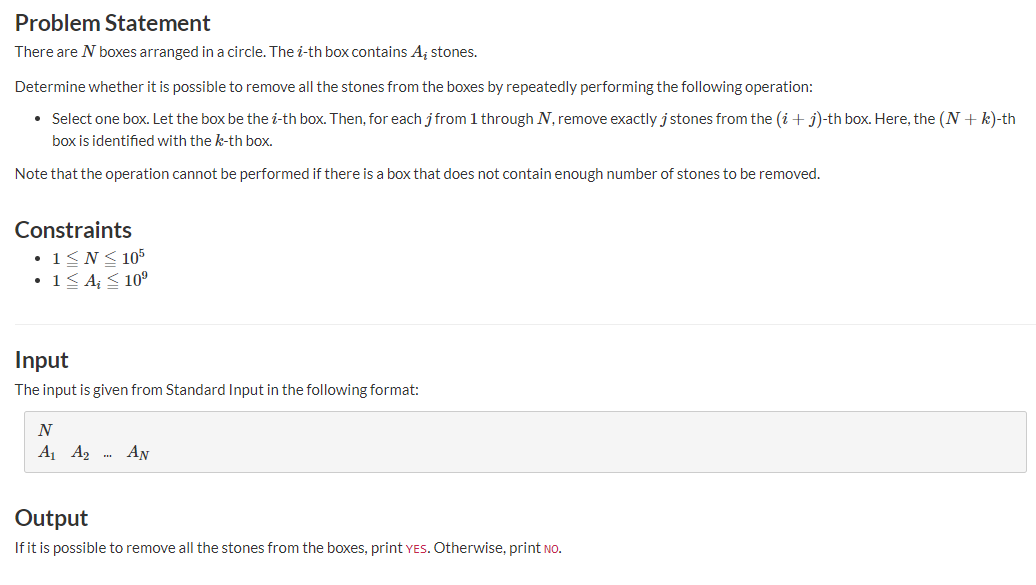
解法：

这种判断能否合法的题,得往数学式子那边想...

----------


每次操作数组的总值一定减少t=n*(n+1)/2,因此数组的和sum必须是t的倍数,否则无解.

设总操作次数为tot=sum/t.

由于相邻数的差值变化要么为1,要么为n-1,
容易想到可能差分数组有关:d[i]=a[i]-a[i-1].

设s[i]为以i为起点的操作次数,那么有式子:
d[i]=s[i]*(n-1)-(tot-s[i]),
解得d[i]=(n*s[i]-t),s[i]=(d[i]+tot)/n,
因此当(d[i]+tot)%n!=0或(d[i]+tot)/n<0时,无解.

其他情况有解.

参考:
https://www.luogu.com.cn/blog/ryoku/solution-at2303

code：

#include <bits/stdc++.h>
#define int long long
#define PI pair<int,int>
using namespace std;
const int maxm=2e6+5;
int a[maxm];
int n;
void solve(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    int sum=0;
    for(int i=1;i<=n;i++){
        sum+=a[i];
    }
    int t=n*(n+1)/2;
    if(sum%t){
        cout<<"NO"<<endl;
        return ;
    }
    int tot=sum/t;//总操作次数
    a[0]=a[n];
    for(int i=1;i<=n;i++){
        int dif=a[i]-a[i-1];
        if((tot-dif)%n||(tot-dif)/n<0){
            cout<<"NO"<<endl;
            return ;
        }
    }
    cout<<"YES"<<endl;
}
signed main(){
    ios::sync_with_stdio(0);
    solve();
    return 0;
}

最后

以上就是坚强黑夜为你收集整理的AGC010 B - Boxes（思维，数学）的全部内容，希望文章能够帮你解决AGC010 B - Boxes（思维，数学）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。