einsum爱因斯坦求和0. 爱因斯坦求和约定（Einstein Notation）1. 转置2. 全部元素求和3. 某一维度求和4. 矩阵对应维度相乘(广播形式)5. 矩阵对应维度相乘(求和形式)6. 矩阵点积7. 矩阵外积(相乘)8. Tensor实例中的应用（PyTorch）

63 阅读 0 评论 42 点赞

我是靠谱客的博主爱撒娇眼神，最近开发中收集的这篇文章主要介绍einsum爱因斯坦求和0. 爱因斯坦求和约定（Einstein Notation）1. 转置2. 全部元素求和3. 某一维度求和4. 矩阵对应维度相乘(广播形式)5. 矩阵对应维度相乘(求和形式)6. 矩阵点积7. 矩阵外积(相乘)8. Tensor实例中的应用（PyTorch），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

https://zhuanlan.zhihu.com/p/74462893

0. 爱因斯坦求和约定（Einstein Notation）

在数学中，爱因斯坦求和约定是一种标记法，也称为Einstein Summation Convention，在处理关于坐标的方程式时十分有效。简单来说，爱因斯坦求和就是简化掉求和式中的求和符号，即 [公式] ,这样就会使公式更加简洁，如

Numpy是Python中的一个重要的科学计算库，支持大量的多维数组计算，并提供了大量的运算函数库。Numpy率先将爱因斯坦求和以扩展函数的方式引入(np.einsum)，而多维数组的特性又非常符合深度学习中张量（Tensor）的特性，因此，基于Numpy，TensorFlow、PyTorch等深度学习框架也纷纷将einsum作为其拓展函数，与Numpy相比，tf和torch中参与运算的张量具有梯度，可以进行反向传播。

对于张量/矩阵运算，einsum几乎无所不能，以下以Numpy为例，来说明其典型用法，PyTorch和TensorFlow中的用法大同小异。

1. 转置

import numpy as np
a = np.arange(0, 9).reshape(3, 3)
print(a)
b = np.einsum('ij->ji', a)
print(b)

Output:
a: [[0 1 2]
 [3 4 5]
 [6 7 8]]
b: [[0 3 6]
 [1 4 7]
 [2 5 8]]

2. 全部元素求和

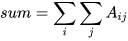
import numpy as np
a = np.arange(0, 9).reshape(3, 3)
print(a)
b = np.einsum('ij->', a)
print(b)

Output:
a: [[0 1 2]
 [3 4 5]
 [6 7 8]]
b: 36

3. 某一维度求和

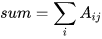
import numpy as np
a = np.arange(0, 9).reshape(3, 3)
print(a)
b = np.einsum('ij->i', a)
print(b)

Output:
a: [[0 1 2]
 [3 4 5]
 [6 7 8]]
b: [ 3 12 21]

4. 矩阵对应维度相乘(广播形式)

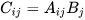
import numpy as np
a = np.arange(0, 12).reshape(3, 4)
print(a)
b = np.arange(0, 4).reshape(4)
print(b)
c = np.einsum('ij,j->ij', a, b)
print(c)

Output:
a: [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
b: [0 1 2 3]
c: [[ 0  1  4  9]
 [ 0  5 12 21]
 [ 0  9 20 33]]

5. 矩阵对应维度相乘(求和形式)

import numpy as np
a = np.arange(0, 12).reshape(3, 4)
print(a)
b = np.arange(0, 4).reshape(4)
print(b)
c = np.einsum('ij,j->i', a, b)
print(c)

Output:
a: [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
b: [0 1 2 3]
c: [14 38 62]

6. 矩阵点积

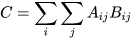
import numpy as np
a = np.arange(0, 12).reshape(3, 4)
print(a)
b = np.arange(0, 12).reshape(3, 4)
print(b)
c = np.einsum('ij,ij->', a, b)
print(c)

Output:
a: [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
b: [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
c: 506

7. 矩阵外积(相乘)

import numpy as np
a = np.arange(0, 12).reshape(3, 4)
print(a)
b = np.arange(0, 12).reshape(4, 3)
print(b)
c = np.einsum('ik,kj->ij', a, b)
print(c)

Output:
a: [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
b: [[ 0  1  2]
 [ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]]
c: [[ 42  48  54]
 [114 136 158]
 [186 224 262]]

8. Tensor实例中的应用（PyTorch）

情境如下：

有两个tensor A和B，size都是[16, 8, 5, 128, 128]，想将两者的第2个维度，即size为5的维度，分别reshape为5x1和1x5的两个向量，然后计算外积，得到一个5x5的kernel。但是，在张量中进行这样的运算，同时保持其他维度不受影响，是比较困难的，而einsum可以完美就觉这种情况。

首先，A可以view成一个size为[18, 8, 5, 1, 128, 128]的tensor, 同理，B可以view为size为[16, 8, 1, 5, 128, 128]的tensor，此时，结果为可以表示为

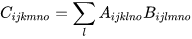
这是一个复杂版的乘法，相对应的PyTorch代码如下：

import torch
A = torch.randn(16, 8, 5, 128, 128)
B = torch.randn(16, 8, 5, 128, 128)
print('A:', A.size())
print('B:', B.size())
A = A.unsqueeze(3)
B = B.unsqueeze(2)
print('Viewed A:', A.size())
print('Viewed B:', B.size())
C = torch.einsum('ijklno,ijlmno->ijkmno', [A, B])
print('C:', C.size())

Output：
A: torch.Size([16, 8, 5, 128, 128])
B: torch.Size([16, 8, 5, 128, 128])
Viewed A: torch.Size([16, 8, 5, 1, 128, 128])
Viewed B: torch.Size([16, 8, 1, 5, 128, 128])
C: torch.Size([16, 8, 5, 5, 128, 128])

欢迎关注知乎专栏【深度图像与视频增强】，一起交流、探讨计算机视觉中的一些问题。