复习链接

计算机算法设计与分析第一章思维导图
计算机算法设计与分析第二章思维导图&&知识点总结
计算机算法设计与分析第三章思维导图&&知识点总结
计算机算法设计与分析第四章思维导图&&知识点总结
计算机算法设计与分析第五章思维导图&&知识点总结 ( 初稿 )
计算机算法设计与分析第六章思维导图&&知识点总结 ( 初稿 )
计算机算法设计与分析第七章思维导图&&知识点总结 ( 初稿 )

思维导图

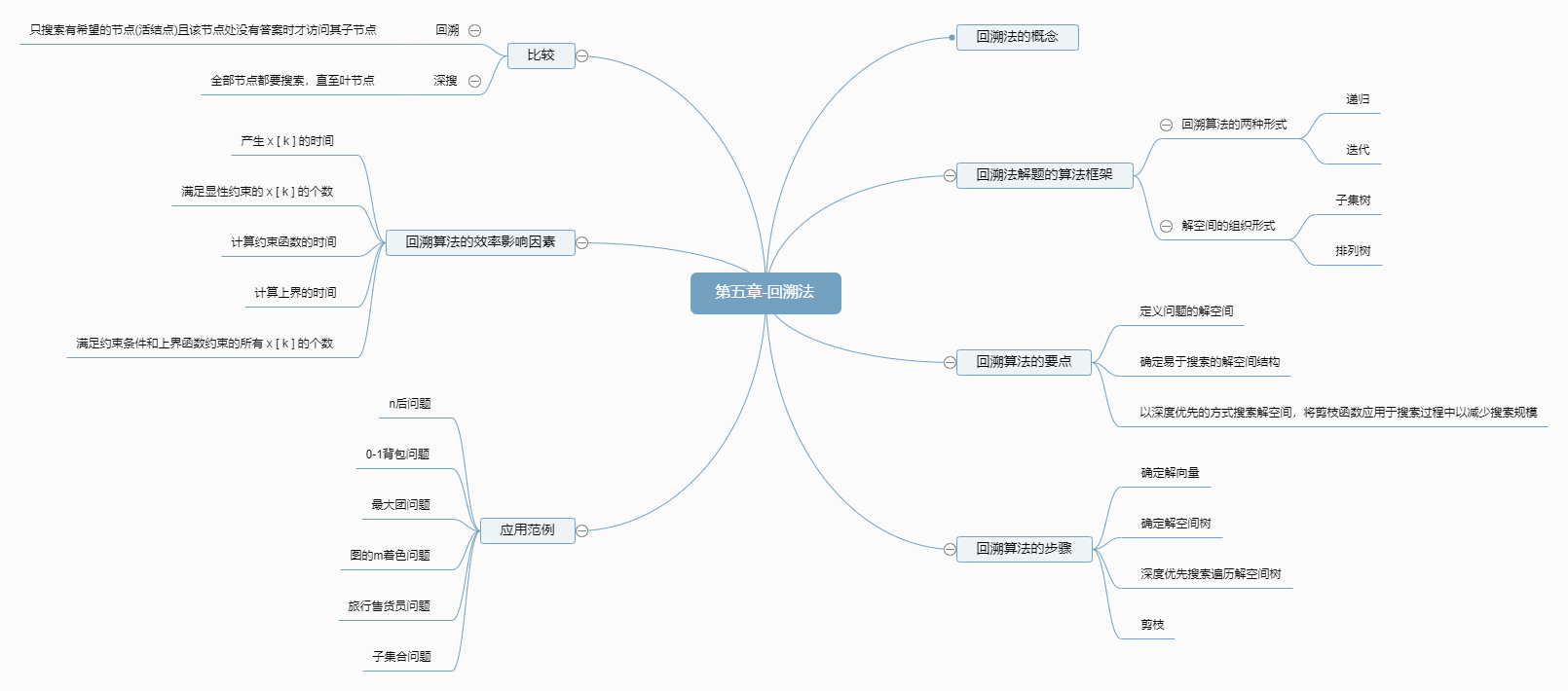
回溯法的概念

回溯法（ 探索与回溯法 ）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

回溯法解题的算法框架

回溯算法的两种形式

（1）递归
（2）迭代

解空间的组织形式

（1）子集树：

当所给问题是从n个元素的集合S中找出满足某种性质的子集时，相应的解空间为子集树

（2）排列树：

当所给问题是确定n个元素满足某种性质的排列时，相应的解空间树被称为排列树

回溯算法的要点：

（1）定义问题的解空间
（2）确定易于搜索的解空间结构
（3）以深度优先的方式搜索解空间，将剪枝函数应用于搜索过程中以减少搜索规模

回溯算法的步骤：

（1）确定解向量
（2）确定解空间树
（3）深度优先搜索遍历解空间树
（4）剪枝

回溯法与深度优先搜索的比较

回溯：
只搜索有希望的节点(活结点)且该节点处没有答案时才访问其子节点

深度优先搜索：
全部节点都要搜索，直至叶节点

回溯算法的效率影响因素

产生 x [ k ] 的时间
满足显性约束的 x [ k ] 的个数
计算约束函数的时间
计算上界的时间
满足约束条件和上界函数约束的所有 x [ k ] 的个数

应用范例

n后问题

解空间：完全 n 叉树
思路：

数组 x 表示 n 后问题的解。x [ i ] 表示皇后 i 放在棋盘第 i 行的第 x [ i ] 列。
对于皇后 i 与 j ，一行放一个即 i != j ，解决行内冲突，一列放一个即 x [ i ] != x [ j ] ,解决列内冲突，abs ( i - j ) != abs ( x [ i ] - x [ j ] ) 则表示不在同一斜线上，解决斜线冲突。
回溯解决 n 后问题，完全 n 叉树表示解空间。同时，利用可行性约束减去不满足行、列和斜线约束的子树。

非递归版本：

数组 x 记录解空间树中从根到当前扩展结点的路径，这些信息已包含回溯法在回溯所需要的空间。利用数组 x 所含的信息，可将上述回溯法表示成非递归的形式，进一步省去 O（ n ）递归栈空间。

0-1背包问题

解空间：子集树
思路：

0 - 1 背包问题的解空间可用子集树表示。在搜索解空间树时，只要其左儿子节点是一个可行节点，搜索就进入其左子树。当右子树中有可能包含最优解时才进入右子树搜索；否则将右子树剪去。若当前体积超过最大体积剪去，若当前价值加上剩余体积做分数背包的最大价值小于当前最大价值，那么剪去。

时间复杂度O（ n * 2 ^ n ）

最大团问题

解空间：子集树
设当前扩展结点 Z 位于解空间树的第 i 层。在进入左子树前，必须确认从顶点 i 到已选入的顶点集中每个顶点都有边相连。在进入右子树前，必须确认还有足够多的可选择顶点，使得算法有可能在右子树中找到更大的团。

图的m着色问题

解向量：x [ 1 ] … x [ n ] ，x [ i ] 表示 i 节点的颜色
解空间：高度 n + 1 的完全 m 叉树
枚举每个节点可行的颜色，同时检查可行性 ( 这个节点此时的颜色与跟它相邻的节点的颜色都不同 ) ，若是可行即可继续递归枚举下一节点的颜色。当所有节点都枚举完，此时的 x 就是合理的染色方案。

旅行售货员问题

解向量：x [ 1 ] … x [ n ] ，x [ i ] 表示第 i 步走到那个点
解空间：排列树
每次进行下一步时，先判断下一节点有没有走过，若走过就剪去，然后再判断当前的花费代价加上这条边的代价会不会比已有的最小代价大，若大就剪去。

子集合问题

解空间：子集树
思路：

此题与 0 - 1 背包类似，每个物品分为选与不选两种状态。
回溯过程中若所选取的总价值 > c 则剪去，若当前价值 + 剩下所有数的价值都达不到 c ，那么也剪去。

最后

以上就是无心哈密瓜为你收集整理的计算机算法设计与分析第五章思维导图&&知识点总结 ( 初稿 )复习链接思维导图回溯法的概念回溯法解题的算法框架回溯算法的要点：回溯算法的步骤：回溯法与深度优先搜索的比较回溯算法的效率影响因素应用范例的全部内容，希望文章能够帮你解决计算机算法设计与分析第五章思维导图&&知识点总结 ( 初稿 )复习链接思维导图回溯法的概念回溯法解题的算法框架回溯算法的要点：回溯算法的步骤：回溯法与深度优先搜索的比较回溯算法的效率影响因素应用范例所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。