前言

一、傅里叶变换的作用

1.傅里叶变换的直观理解

如果你在网上看过以下关于傅里叶变换的资料：
傅里叶分析之掐死教程（完整版）更新于2014.06.06
Python 中 FFT 快速傅里叶分析
形象理解二维傅里叶变换
【numpy】几种fft函数的使用
那么相信你已经对傅里叶变换有了基本的认识，如果没有看过也没关系！就我而言，我其实不需要深入了解傅里叶变换的原理，但又不得不必须学会如何使用FFT对采样的数据进行处理并得到最终的图像，比如频谱图，比如色散图。所以，对于傅里叶变换的作用的直观理解，应该是从它的结果图像中来理解。比如在频谱图中，可以看到原始信号中每个频率分量的占比情况，根据频率带宽的分布可以得到系统允许频率和禁止频率。
维基百科上的这个图像很形象表达了傅里叶变换的作用：时域上复杂的原始信号可以分解成在时域上不同频率和振幅的简单的正弦波，而把分解得到每一个正弦波的频率的和对应的振幅绘制出来，即可得到傅里叶变换的结果即频谱图$\tilde{A}(f)$。

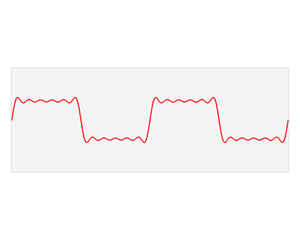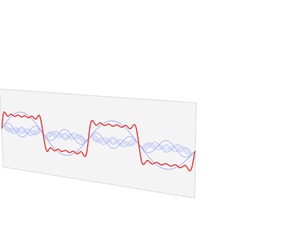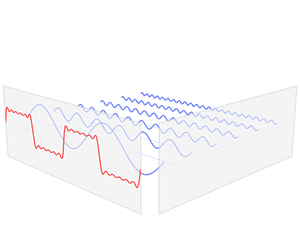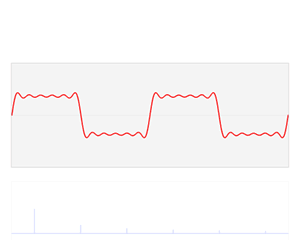
对于获取原始信号中的频率分量的过程，其实我觉得还有一个非常直观例子，即三棱镜对白光的色散：

当一束白光（输入的原始信号）经过三棱镜后，三棱镜会将白光展开为不同的颜色（输出的各个频率的波）。那么傅里叶变换的作用也就好比三棱镜，当原始信号进行傅里叶变换后，就可以获取组成原始信号的频率贡献情况。

2.傅里叶变换家族

针对原始信号在时域上是否连续，是否周期的情况，傅里叶变换家族出现了四种获取相应频谱的方法：

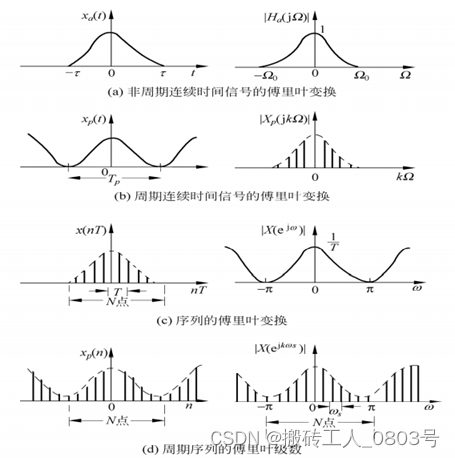
（a）连续傅里叶变换（FT）：在时域上连续的，非周期的波形，经过FT之后，得到的频谱是连续的，非周期的。
（b）连续傅里叶级数（FS）：在时域上连续的，周期的波形，经过FS之后，得到的频谱是离散的，非周期的。
（c）离散傅里叶变换（DTFT）：在时域上离散的，非周期的波形，经过DTFT之后，得到的频谱是连续的，周期的。
（d）离散傅里叶级数（DFS）：在时域上离散的，周期的波形，经过DFS之后，得到的频谱是离散的，周期的。

就实际情况而言，我们对原始信号经过等时间间隔采样并保存得到的都是在时域上离散的数值，而且计算机对这些输入的离散数值进行傅里叶变换之后的得到的结果也是且只能是离散的数值。因此，看起来以上四种方法中适合计算机使用的只有DFS，只有该方法的输入输出都是离散数值，但由于它对输入的离散数值具有周期性的要求，所以又有了它的改进方法即DFT，这种方法对输入的离散数值没有特别的限制，大多数情况所说的傅里叶变换就是指DFT。DFT会对输入的离散数值进行如下运算：
假设对一时变信号进行采样后得到N个数值：$x(0)，x(1)，x(2)...x(N-1)$，那把这N个数值作为DFT的输入，对于N个输入的数值来说：
$$f(k)=\sum _{n=0}^{N-1}x(n)\cdot e^{-j\cdot \frac{2\pi \cdot n}{N}\cdot k},k=0，1，\mathrm{2...}N-1$$
这个公式表示：①假设DFT有N个输入数值的话，那么经过傅里叶变换后也得到了N个输出点，因此频谱图中就有N个点。

②式中的$e^{-j\cdot \frac{2\pi \cdot n}{N}\cdot k}$是一个复数，因此DFT的结果也是一个复数。但是对于第一个输出点$f(k=0)$来说，它的DFT的结果值为 $f(0)=\sum _{n=0}^{N-1}x(n)\cdot e^{-j\cdot \frac{2\pi \cdot n}{N}\cdot 0}=x(0)+x(1)+x(2)+...+x(N-1)$ ，即第一个点的DFT结果是一个实数值。

③对于输出的每一个点来说，DFT都需要进行N次运算，对于总共有N个输入的采样值来说，那么DFT的算法运算复杂度为$O(N^2)$。可见输入的点数越多，运算次数也越多。

囿于原始DFT算法的运算速度，于是一种用于加速DFT计算的算法横空出世，那就是快速傅里叶变换（FFT），相比DFT，它的运算复杂度为$NlogN$，当输入的采样点数越多，FFT算法的速度相比原始的DFT快得多。所以在程序的数学库中用于一维傅里叶变换的函数为fft()，该函数便实现了上式的运算流程。

二、时间、空间、时空的傅里叶变换

1.时间的傅里叶变换

首先需要明白一点，用于当做时间傅里叶变换的输入的采样值是怎么获得的？在现实世界中，或者通过示波器的探头接触某个器件的输出位置点进行等时间间隔采样，以此获得N个随时间变化的采样值；或者通过放在空间中某一位置点的传感器等时间间隔采样，也能获取N个随时间变化的采样值。。。它们都有一个特点：把空间固定为一点，只等时间间隔采样在该空间位置点上的原始输出信号。

假设原始信号的最高频率分量为f（非角频率w），时间采样频率为Fs_time，采样点数为N。
以上三个条件之间有如下关系：①根据奈奎斯特采样定理，采样频率至少是原始信号的最高频率分量的两倍，即$Fs\_time\ge 2\ast f$。②采样频率的倒数即采样周期Ts，采样周期乘以采样点数就是采样时间。
接下来，将从时间的FFT得到的频谱图为切入点，来讲解如何获取频谱图中每一个点，并绘制出频谱图的基本流程。
首先得到频谱图中每个点的横坐标：
对N个采样数值进行FFT后，也有N个复数结果值：$f(k)，k=0，1，\mathrm{2..}N-1$，它们对应N个频率点，这些频率点对应的频率值为$\frac{Fs\_time}{N}\cdot k$ ,其中$\frac{Fs\_time}{N}$称为频率分辨率，即频谱图（$\tilde{A}(f)$）中的两个点横坐标之间的最小间隔，因此要得到更小的频率分辨率（也就是让频谱曲线看起来更加连续），就只能增加采样点数（但不能降低采样频率），也就是延长采样时间。
比如当频率点k=0时，其代表的频率值即为$f=\frac{Fs\_time}{N}\cdot 0$ = 0Hz，当频率点k=1时，其代表的频率值即为$f=\frac{Fs\_time}{N}\cdot 1$ = $\frac{Fs\_time}{N}$Hz。。。于是便得到了频谱图中所有点的横坐标。显然，如此计算的话，频谱图中的点的最大横坐标为Fs_time，也就是说，频谱图的横轴范围是受时间采样频率Fs_time影响的。
接着是得到频谱图中每个点的纵坐标：
对于FFT得到的除了第一个点（0Hz）以外的所有频率点，其傅里叶振幅$\tilde{A}$为：首先对该点的复数结果取模，接着再除以采样点数N，最后再乘以2即可。对于第一个点（即直流分量0Hz），它的傅里叶振幅为取模之后，只除以采样点数N即可。如此，便得到了频谱图（$\tilde{A}(f)$）的N个点的纵坐标。
看起来有了频谱图中每个点的横坐标和纵坐标，按理说就可以绘制出一个完整的频谱图了。但是，实际上，对于FFT之后的前面一半的频率点k=0，，，$\frac{N}{2}-1$，它们对应的频率确实为0Hz，，，$\frac{Fs\_time}{N}\cdot (\frac{N}{2}-1)$Hz，但是对于后一半部分的频率点k=$\frac{N}{2}$，，，N-1，它们对应的频率为$-\frac{N}{2}\cdot \frac{Fs\_time}{N}$，，，$-\frac{Fs\_time}{N}$。显然对于时间的傅里叶变换得到的频谱图来说，负频率没有物理意义，所以需要舍弃负频率的点，使频谱图的宽度减少一半。

什么，你居然问我怎么晓得如此操作的，有什么依据吗？

其实，网上关于傅里叶变换的资料众多，质量也是参差不齐，让人找不到北，而恰好MATLAB官方的fft()函数的文档中有关于时间的傅里叶变换的例程，见MATLAB官方参考链接，这个示例演示了如何获取频谱。而更巧的是Python的Numpy库的fft()例程居然没有获取信号频谱的例子，那我就搬一下砖，直接将MATLAB官方的傅里叶变换的例程移植到Python程序中，如下：

#################
#author:YQYUN
#date:22/6/18
#desc:从MATLAB官方例程移植而来，演示时间的傅里叶变换
#desc:固定空间为一个点，得到在这个位置点上采样得到时间范围内的信号
#################

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pylab import mpl

mpl.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文
mpl.rcParams['axes.unicode_minus'] = False  # 显示负号

#时间采样频率
Fs_time =1000
#采样周期
T = 1/Fs_time
#采样点数
M = 1500
#采样时间序列
t = np.arange(0, M-1) * T

# 设置需要采样的信号
y = 0.7 * np.sin(2 * np.pi * 50 * t)+np.sin(2 * np.pi * 120 * t)
#加入噪声信号
y = y + 2 * np.random.randn(np.size(t))

#画原始波形
plt.subplot(121)
plt.plot(1000*t[0:50], y[0:50])
plt.xlabel('t(s)')
plt.ylabel('A')
plt.title('原始波形')

#快速傅里叶变换得到一个复数序列，取复数的绝对值，即复数的模(双边频谱)
abs_y = np.abs(np.fft.fft(y))
#除了第一个点（0Hz）外，对模值要先除以采样点数量，再乘以2
fft_y = abs_y / M * 2
#对于第一个点（0Hz），只需对模值除以采样点数量即可 
fft_y[0] /= 2
#幅度取一半区间（单边频谱）
fft_y = fft_y[0:int(M / 2)]
#频率取一半区间
F = np.arange(0,int(M / 2)) * Fs_time / M

#将FFT结果保存到文件
FFTResult_time = np.zeros((int(M / 2),2))
FFTResult_time[:,0] = F[:]
FFTResult_time[:,1] = fft_y[:]
np.savetxt('FFTResult_time.txt', FFTResult_time,delimiter=' ')
print('时间FFT结果已经写入FFTResult_time.txt，第一列为频率，第二列为振幅')

#画图
plt.subplot(122)
plt.plot(F, fft_y)
plt.xlabel('f(Hz)')
plt.ylabel('A')
plt.title('单边频谱')
plt.show()

首先看一下运行结果，对比MATLAB（上）和Python（下）的结果，如下：

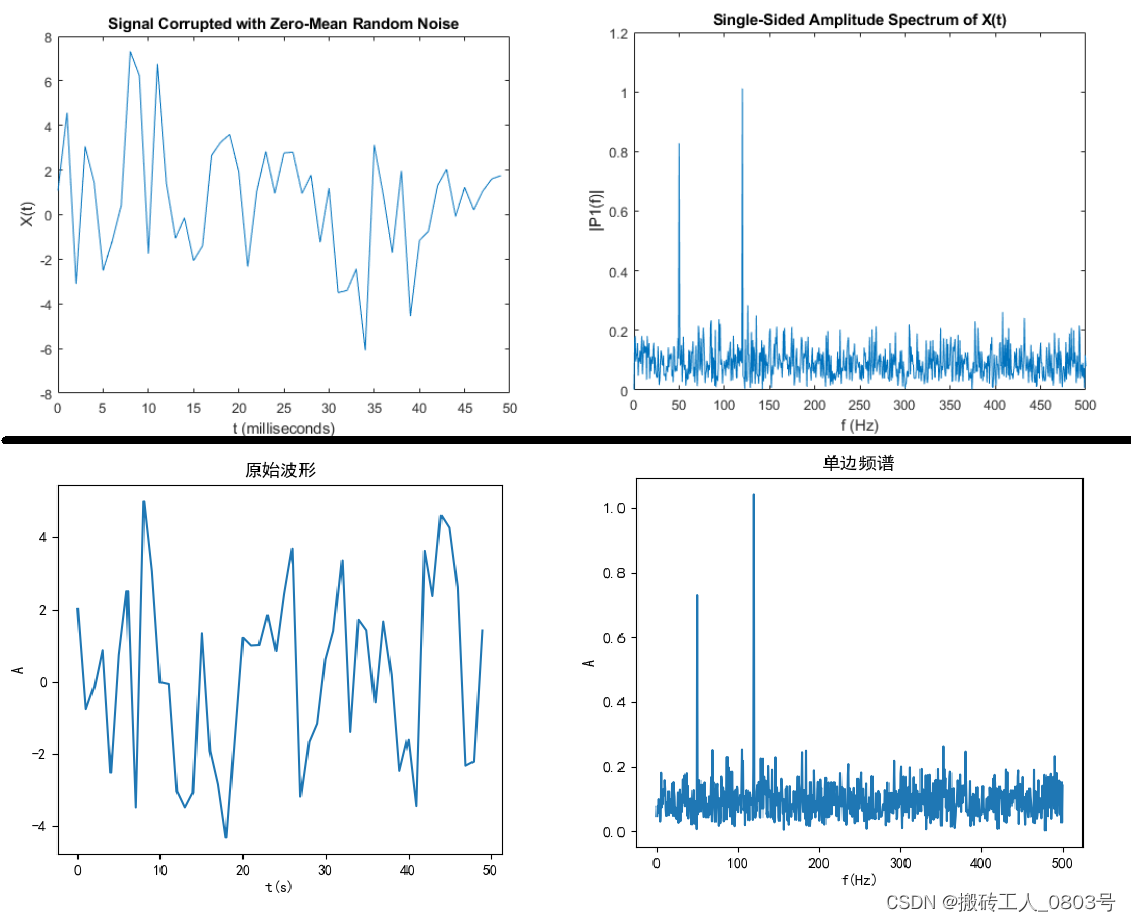
由于加入了随机的噪声信号，所以两者的时域波形是不一样的，比如再次运行一下这个程序：

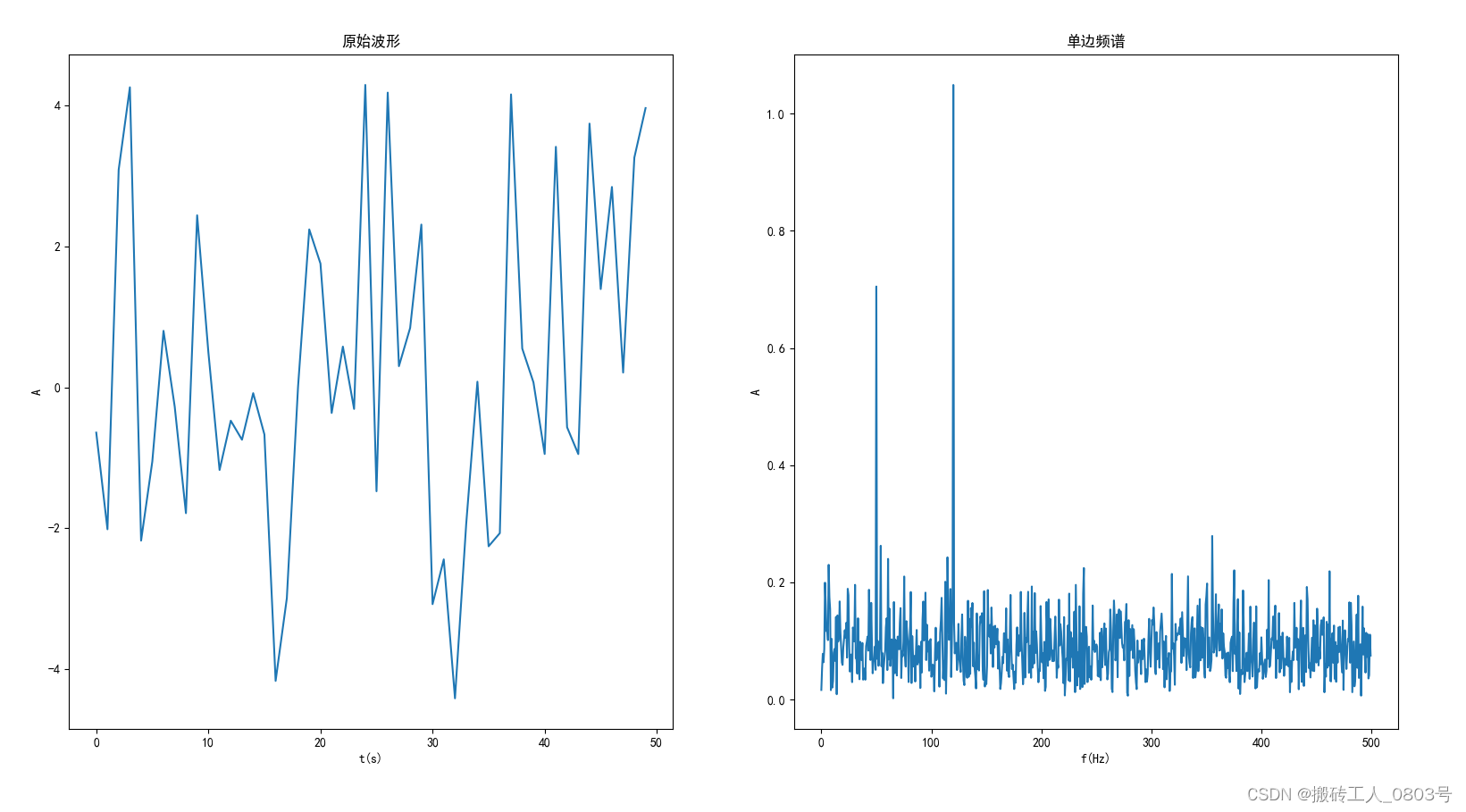
以上三个图像的时域波形看起来都是乱七八糟的，没有什么规律可言，但是从它们的频谱图中可以很明显的看出50和120Hz频率分量的对整个频谱图的贡献。傅里叶变换为我们提供了另一种视角来观测世界。

首先是构造对原始信号进行等时间间隔采样获得的数值，此处以振幅A=0.7，频率f=50Hz，和A=1，f=120Hz的正弦波为基础波形，然后加入一个随机噪声，从而生成一个随着采样时间变化的函数，在规定的采样频率和采样点数M=1500个的条件下即可通过这个函数生成采样值。总共需要的采样时间为采样周期T乘以采样点数M。此处要注意进行傅里叶变换的前提条件：采样频率Fs_time设置为信号需要识别的最高频率分量的两倍以上，此处为Fs_time=1000Hz（原始波形中除噪声外的最高频率f=120Hz）。

#时间采样频率
Fs_time =1000
#采样周期
T = 1/Fs_time
#采样点数
M = 1500
#采样时间序列
t = np.arange(0, M-1) * T
# 设置需要采样的信号
y = 0.7 * np.sin(2 * np.pi * 50 * t)+np.sin(2 * np.pi * 120 * t)
#加入噪声信号
y = y + 2 * np.random.randn(np.size(t))

将M个采样值作为函数fft()的输入参数，并将输出的复数结果取模得到abs_y ，然后按照上文所述的那样，对输出结果的第一个值（0Hz）和其他值分别处理，得到每个频率点的傅里叶振幅fft_y，也就是频谱图中每一个点的纵坐标。接着是将频率分辨率分别乘以频率点以获取每个频率点对应的频率值，也就是频谱图中每一个点的横坐标。最后舍弃掉频谱图的后一半部分的数据，即负频率的部分，只保留fft_y和F序列的前一半区间 。

#快速傅里叶变换得到一个复数序列，取复数的绝对值，即复数的模(双边频谱)
abs_y = np.abs(np.fft.fft(y))
#除了第一个点（0Hz）外，对模值要先除以采样点数量，再乘以2
fft_y = abs_y / M * 2
#对于第一个点（0Hz），只需对模值除以采样点数量即可 
fft_y[0] /= 2
#幅度取一半区间（单边频谱）
fft_y = fft_y[0:int(M / 2)]
#频率取一半区间
F = np.arange(0,int(M / 2)) * Fs_time / M

如此便得到了频谱图中每个点的横坐标和纵坐标，那么可以直接使用绘图库的函数绘制这些点。若要保存频谱图的话，则可以将每一个点的横坐标和纵坐标装进一个$\frac{M}{2}$行，2列的矩阵中，其中第一列放点的横坐标，第二列放点的纵坐标。最后调用savetxt()函数保存该矩阵即可。

#将FFT结果保存到文件
FFTResult_time = np.zeros((int(M / 2),2))
FFTResult_time[:,0] = F[:]
FFTResult_time[:,1] = fft_y[:]
np.savetxt('FFTResult_time.txt', FFTResult_time,delimiter=' ')
print('时间FFT结果已经写入FFTResult_time.txt，第一列为频率，第二列为振幅')

对于不了解MATLAB的人来说，可能对MATLAB官方程序的这行代码感到奇怪：

P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);

这是由于在MATLAB中，数组的下标是从1开始的，而其他语言都是从0开始的，在移植MATLAB代码时需要注意。

2.空间的傅里叶变换

网上关于时间的傅里叶变换的资料是最多的，耐心查阅的话，不难搞明白它的使用技巧。接下来将介绍空间的傅里叶变换，以平面波为例，平面波的形式为$y=A\cdot sin(w\cdot t-k\cdot x)$，其中k是波矢，稍微展开一下：
$$y=A\cdot sin(2\pi \cdot f\cdot t+2\pi \cdot (-\frac{1}{\lambda })\cdot x)$$
其中的时间项为$2\pi \cdot f\cdot t$，空间项为$2\pi \cdot (-\frac{1}{\lambda })\cdot x$，表示函数值y是随着时间和空间变化的。

在上文中，把空间固定为一点，等时间间隔采样得到该空间位置点上的原始信号在某一时间范围内的数值，该一维序列经过FFT后，得到了（$\tilde{A}(f)$）图。时间和空间是等同地位的，通过类比，固定时间为一个时刻，在这个时刻，等空间间隔采样得到随空间变化的一维数值序列，然后对这个一维序列进行傅里叶变换，即可得到（$\tilde{A}(-\frac{1}{\lambda })$）的图像，不过通常还需要将横坐标$(-\frac{1}{\lambda })$转化为波矢k，即对横坐标进行运算：$(-\frac{1}{\lambda })\cdot (-1)\cdot (2\pi )=k$ ，于是便得到了波矢&振幅图（$\tilde{A}(k)$）。
在时间的傅里叶变换后，舍弃掉了负频率的数据（负频率无意义），但是波矢呢？波矢k是一个矢量，在此处举的例子中，k是在限制在了x轴方向上变化，但它的值有正有负，表示波的传播方向，所以就不能舍弃任何空间傅里叶变换后得到的点。
类比上文时间的傅里叶变换，空间的傅里叶变换示例如下：

#################
#author:YQYUN
#date:22/6/19
#desc:以平面波为例，演示空间的傅里叶变换
#desc:固定时间为一个点，在这个时刻上采样得到空间范围内的信号
#################

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pylab import mpl

mpl.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文
mpl.rcParams['axes.unicode_minus'] = False  # 显示负号

#平面波方程：A*sin(w*t - k*x)

#####构造信号#####

#信号振幅：24
A = 24
#信号频率:8Hz
f = 8
#信号角频率：2*pi*f
w = 2*np.pi*f
#信号波长：2*pi*(1/3)
lamb = 2 * np.pi *(1 / 3)
#信号波矢：2*pi/lamb=3m^-1
k = 2 * np.pi / lamb

#对于固定时间点t=0s，对指定x范围内进行FFT可以得到A'(k)图
t_fixed = 0

#x空间范围：0到98m
x_start,x_end = 0,98

#空间采样率设为信号波长倒数的3倍
Fs_volume = 3 * (1 / lamb)
#采样空间序列
x = np.arange(x_start,x_end,1/Fs_volume)
#空间采样点数
N = np.size(x)

#举例子时注意信号的波矢k'不能大于k
y1 = (A * np.sin(w * t_fixed - k * x) +
    2 * A * np.sin(w * t_fixed - 0.9*k * x) +
    3 * A * np.sin(w * t_fixed - 0.8*k * x) +
    4 * A * np.sin(w * t_fixed - 0.7*k * x))
#画图
plt.subplot(1,2,1)
plt.xlabel('x (m)')
plt.ylabel('A')
plt.plot(x, y1)
plt.title('t=0,原始波形')

#空间的傅里叶变换
fft_y1 = np.fft.fft(y1)
fft_y1 = abs(fft_y1) / N * 2
fft_y1[0] /= 2

#将采样点等间隔分为序列号：0,1,2...N-1：np.arange(-int(N / 2),int(N / 2))
#最终波矢点为k_min...0...k_max共N个

#这里调用一种现成的函数，fftfreq的第一个参数为采样点数，第二个参数为采样频率
#波长的倒数：波数，对比时间项wt=2*pi*f和空间项-kx=2*pi*(-1/lamb)，可知得到的波数要乘以-1
wave_num = -1 * np.fft.fftfreq(N,1/Fs_volume)
#波数*2*pi等于波矢
kx = wave_num * (2 * np.pi)


#保存数据
#重新排序数据，让横轴按照从小到大的顺序存储
kx_sorted = np.sort(kx)
temp_y = np.zeros((N,1))
for i in range(0,N):
    temp_kx = kx_sorted[i]
    #kx里面没有重复元素，故可以这么查找
    kx_index = np.where(kx== temp_kx)
    temp_y[i,0] = fft_y1[kx_index]
kx[0:N] = kx_sorted[0:N]
fft_y1[0:N] = temp_y[0:N,0]

#将FFT结果保存到文件
FFTResult_volume = np.zeros((N,2))
FFTResult_volume[:,0] = kx[:]
FFTResult_volume[:,1] = fft_y1[:]
np.savetxt('FFTResult_volume.txt', FFTResult_volume,delimiter=' ')
print('空间FFT结果已经写入FFTResult_volume.txt，第一列为波矢（2*pi/lambda），第二列为振幅')

#画图
plt.subplot(1,2,2)
plt.xlabel('kx(m^-1)')
plt.ylabel('A')
plt.plot(kx[0:N], fft_y1[0:N])
plt.title('t=0,K空间')
plt.show()

示例中构造了(波矢,振幅)=(1k,1A),(0.9k,2A),(0.8k,3A),(0.7k,4A)共四组平面波的叠加，但是显然由于固定了时间t为一个数，所以平面波就变成了简单的sin形式。举例子时要注意加入的平面波的波矢k’不能大于待分析波矢的最大值k。

在此处，把时间t设置为0，将波矢的最大值k设置为3/m。将采样的空间范围x_start，x_end 设为0，98m，类比时间傅里叶变换中的时间采样频率Fs_time，空间的采样频率Fs_volume也设为至少是信号波长倒数的2倍，示例中为3倍，如此便可以得到空间的采样点数N。

#信号波长：2*pi*(1/3)
lamb = 2 * np.pi *(1 / 3)
#信号波矢：2*pi/lamb=3m^-1
k = 2 * np.pi / lamb
#对于固定时间点t=0s，对指定x范围内进行FFT可以得到A'(k)图
t_fixed = 0
#x空间范围：0到98m
x_start,x_end = 0,98
#空间采样率设为信号波长倒数的3倍
Fs_volume = 3 * (1 / lamb)
#采样空间序列
x = np.arange(x_start,x_end,1/Fs_volume)
#空间采样点数
N = np.size(x)

序列y1中就保存着N个等空间间隔采样得到的数值。类比平面波方程中的时间项$2\pi \cdot f\cdot t$，时间的傅里叶变换后得到傅里叶振幅$\tilde{A}$与频率 $f$ 的关系，那么空间项$2\pi \cdot (-\frac{1}{\lambda })\cdot x$，相应的，空间的傅里叶变换后会得到傅里叶振幅$\tilde{A}$与 $-\frac{1}{\lambda }$ 的关系。只需稍加处理即可得到傅里叶振幅$\tilde{A}$与波矢 $k$ 的关系。

#将采样点等间隔分为序列号：0,1,2...N-1：np.arange(-int(N / 2),int(N / 2))
#最终波矢点为k_min...0...k_max共N个

#这里调用一种现成的函数，fftfreq的第一个参数为采样点数，第二个参数为采样频率
#波长的倒数：波数，对比时间项wt=2*pi*f和空间项-kx=2*pi*(-1/lamb)，可知得到的波数要乘以-1
wave_num = -1 * np.fft.fftfreq(N,1/Fs_volume)
#波数*2*pi等于波矢
kx = wave_num * (2 * np.pi)

注意：在计算波矢点对应的波矢值时，不同于上文根据频率点自己手动计算频率值，这里使用了一个专门用于根据频率（波矢）点计算频率（波矢）值的函数fftfreq()，只需简单的为该函数指定采样点数（第一个参数）和采样频率的倒数（第二个参数）两个参数即可，比如：

可以看到fftfreq()函数的输出序列为从0到正的最大值，然后是从负的最小值到负的最大值。那么该函数的输出序列就可以直接当做傅里叶变换之后每一个点的横坐标。

有了（$\tilde{A}(k)$）图中的每个点的横坐标之后，对于每个点的纵坐标则和时间的傅里叶变换中的获取纵坐标的方式相同，即把空间采样得到的N个数值作为函数fft()的输入参数，并对复数输出结果进行处理就得到了傅里叶振幅$\tilde{A}$。

#空间的傅里叶变换
fft_y1 = np.fft.fft(y1)
fft_y1 = abs(fft_y1) / N * 2
fft_y1[0] /= 2

如此，一个（$\tilde{A}(k)$）图中所有点的横纵坐标都得到了，就可以开始绘图步骤了。不过为了方便绘图，还需要将图中的每个点按照横坐标从负到0，再到正的顺序排序，否则绘制的曲线会出现闭合（参见fftfreq()函数的输出序列）。
若要保存图像数据，则需要一个N行，2列的矩阵按照第一列保存每个点的横坐标，而第二列保存每个点的纵坐标。

#保存数据
#重新排序数据，让横轴按照从小到大的顺序存储
kx_sorted = np.sort(kx)
temp_y = np.zeros((N,1))
for i in range(0,N):
    temp_kx = kx_sorted[i]
    #kx里面没有重复元素，故可以这么查找
    kx_index = np.where(kx== temp_kx)
    temp_y[i,0] = fft_y1[kx_index]
kx[0:N] = kx_sorted[0:N]
fft_y1[0:N] = temp_y[0:N,0]
#将FFT结果保存到文件
FFTResult_volume = np.zeros((N,2))
FFTResult_volume[:,0] = kx[:]
FFTResult_volume[:,1] = fft_y1[:]
np.savetxt('FFTResult_volume.txt', FFTResult_volume,delimiter=' ')
print('空间FFT结果已经写入FFTResult_volume.txt，第一列为波矢（2*pi/lambda），第二列为振幅')

那么根据以上程序得到的（$\tilde{A}(k)$）图如下：

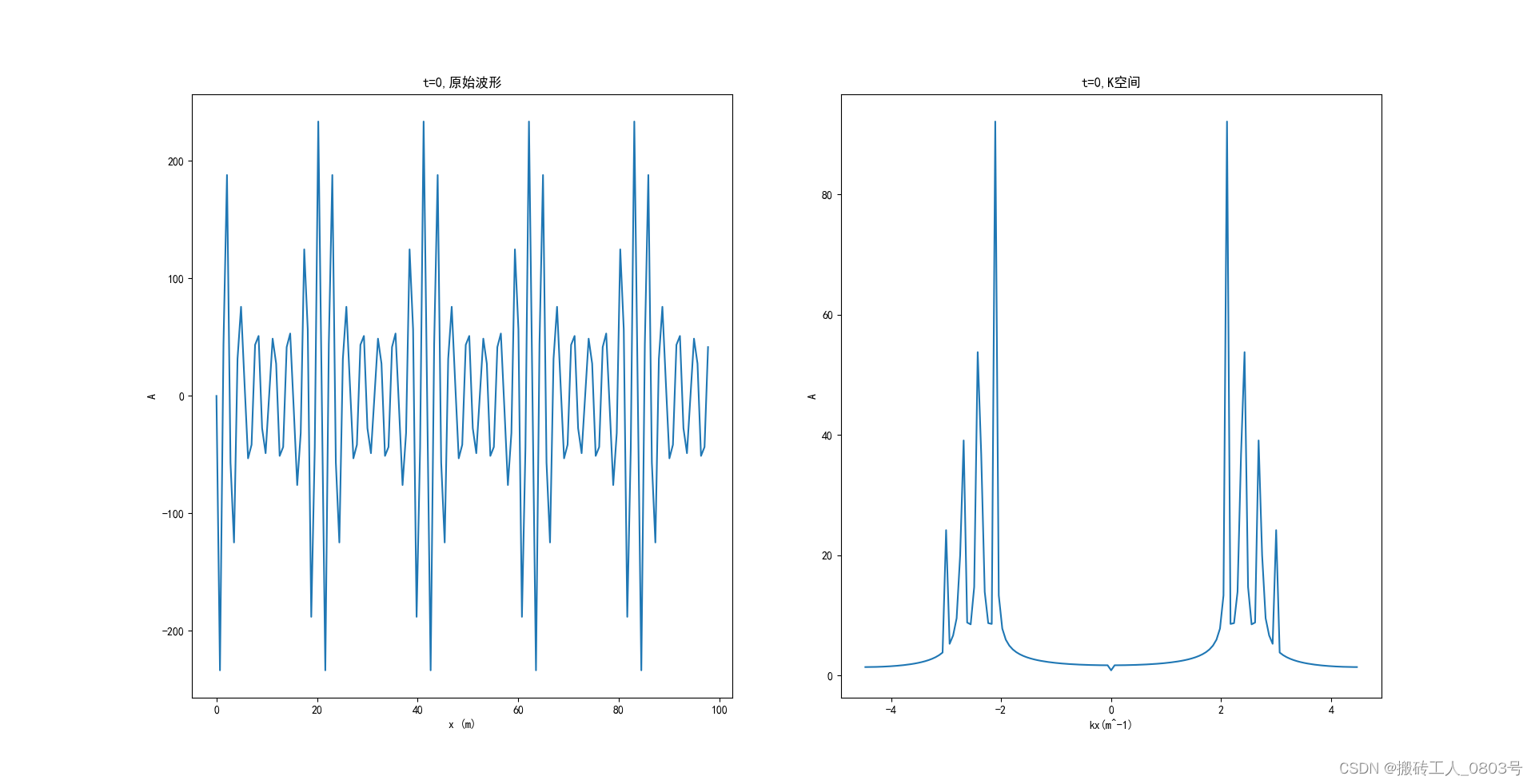
3.时空的傅里叶变换—色散关系

大家都对函数的一维图像，比如$y=A\cdot sin(w\cdot t)$非常熟悉，因为它只有一个自变量t和因变量y。但对于函数的二维图像，比如$y=A\cdot sin(w\cdot t-k\cdot x)$的图像可能不太熟悉，它有两个自变量：时间t和空间x，一个因变量y。要在一个平面坐标系中表示这个二维图像，可以把两个自变量分别映射到两个坐标轴上，于是时间t和空间x的不同组合值，在图像中就表现为点的位置坐标。因变量则可以用颜色来映射它的值，比如使用颜色映射"blue(#0000FF)-white(#FFFFFF)-red(#FF0000)"来表示因变量，那么blue就表示负值，white表示0，red表示正值，而具体的数值则可以按照颜色的深浅来等比例映射表示。如下图表示的是平面波 $y=24\cdot sin(2\cdot \pi \cdot 8\cdot t-3\cdot x)$ 的图像：

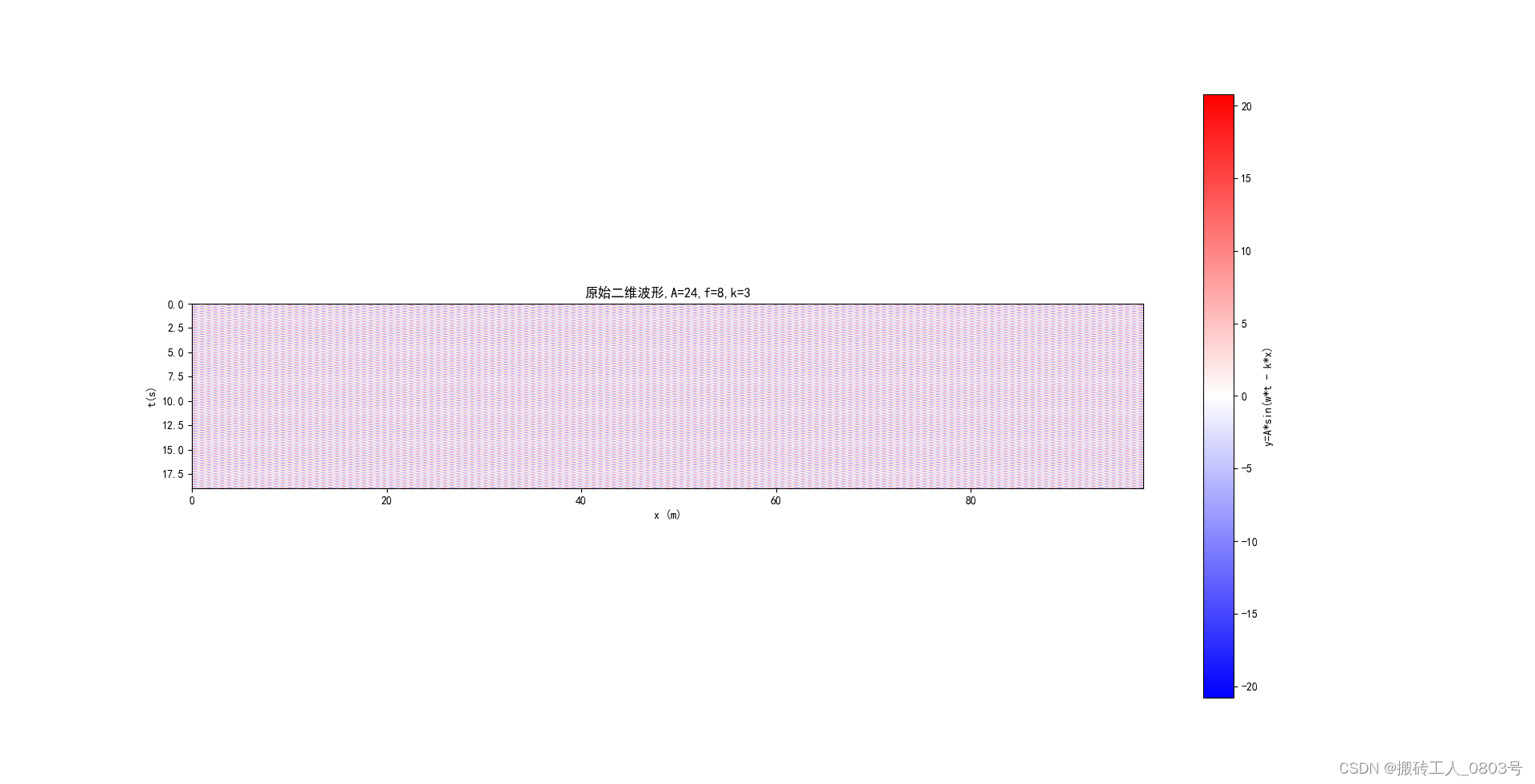
前文介绍的都是一维的傅里叶变换，输入的采样值都是一个1行多列的序列，输出的图像也只是一条曲线。但是色散图，表示的是傅里叶振幅$\tilde{A}$ 与频率$f$ 和波矢$k$ 的关系（即（$\tilde{A}(k,f)$）），它是一个二维的图像，而不是一维的曲线。图像中的每个点的横坐标即该点的波矢值，纵坐标即该点的频率值，而该点的颜色则表示傅里叶振幅$\tilde{A}$。

想当然的，肯定是要同时对时间和空间进行傅里叶变换，即二维FFT，才能得到色散图。正如前文所说，时间的傅里叶变换是将一条以时间为变量的曲线，分解成一系列不同频率，不同振幅的正弦波。那么二维傅里叶变换则是将一个以时间，以空间为变量的二维图像分解成一系列不同频率，不同振幅的平面波。二维傅里叶变换的输入数据应该是在一定时间范围内（图像的纵坐标），一定空间范围内（图像的横坐标）的二维图像，对于图像中的每一个坐标点(x,y)来说（该点的值为f(x,y)），二维傅里叶变换会进行如下运算：
$$F(u,v)=\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}f(x,y)\cdot e^{-j\cdot 2\pi \cdot (\frac{ux}{M}+\frac{vy}{N})}$$
可见对于一个M行N列（输入矩阵）的原始输入图像来说，二维FFT后也会得到一个M行N列（输出矩阵）的输出图像，而且输出的每一个结果F(u,v)也是一个复数。在程序的数学库中用于二维傅里叶变换的函数为fft2()，该函数便实现了上式的运算流程。
上式的直观表现如下图，通过该式子可以得到组成二维图像的不同的平面波贡献：

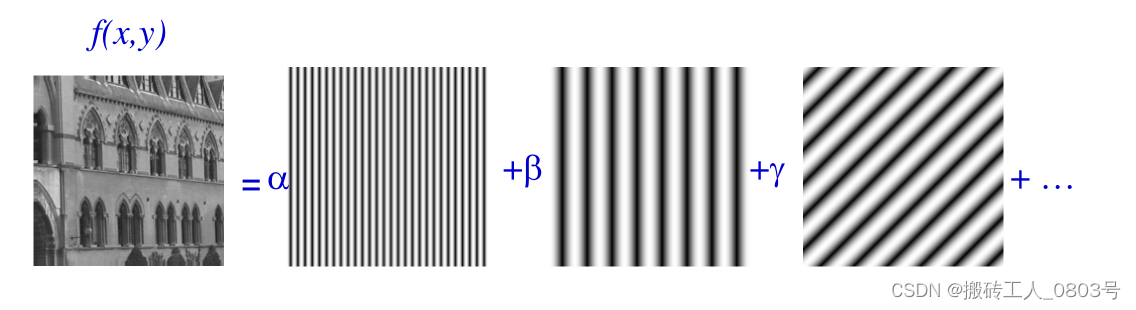
平面波是指波面为平面的波，波矢表示平面波的传播方向，它与波面垂直。由于平面波相对于一维的正弦波来说，除了振幅，频率，相位外，还有一个额外的波矢，所以仍然使用一个复数来表示其振幅和相位，而二维FFT之后得到的矩阵中的每一个点，每一个点的坐标$(u,v)$的则可以表示平面波的法向量，而该向量的模值即$\sqrt{u^2+v^2}$，可用于表示该平面波的频率。比如下图中的$(u,v)$距离中心越远，表示平面波的频率越大，而坐标$(u,v)$则表示垂直于平面波的波面的向量。

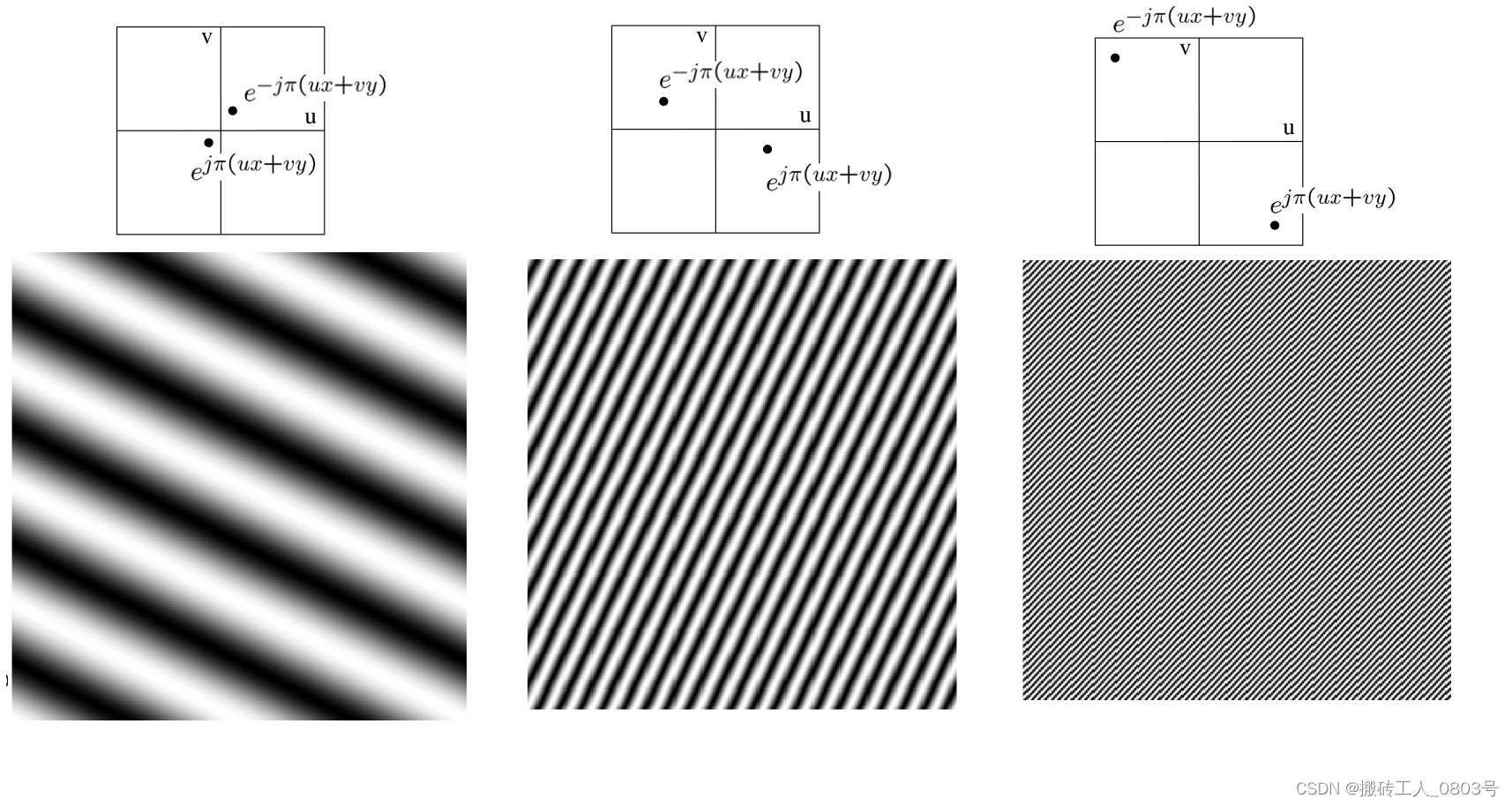
在大概了解二维傅里叶变换的作用后，接着就要考虑如何使用这个工具了。首先是确定二维傅里叶变换的输入，它是一个二维的图像（也就是输入矩阵），输入矩阵中每一个元素的坐标，就表示该点在二维傅里叶变换后得到的输出矩阵中的坐标，而输入矩阵每一个元素的值，则会作为二维傅里叶变换的输入值。以平面波$y=A\cdot sin(2\pi \cdot f\cdot t+2\pi \cdot (-\frac{1}{\lambda })\cdot x)$为例，振幅A=24，空间范围x_start，x_end为0到98m，空间采样率Fs_volume= $3\cdot \frac{1}{\lambda }$，时间范围t_start，t_end为0到19s，时间采样率Fs_time=$3\cdot f$，混合了4个不同频率，不同波矢的平面波：(频率,波矢)=(f,k)，(0.9f,0.9k)，(0.8f,0.8k)，(0.7f,-0.7k)。

#平面波：A*sin(w*t - k*x)

#####构造信号#####

#信号振幅：24
A = 24
#信号频率:8Hz
f = 8
#信号角频率：2*pi*f
w = 2 * np.pi * f
#信号波长：2*pi*(1/3)
lamb = 2 * np.pi *(1 / 3)
#信号波矢：2*pi/lamb=3m^-1
k = 2 * np.pi / lamb

#x空间范围：0到98m
x_start,x_end = 0,98

#空间采样率设为信号波长倒数(波数)的3倍
Fs_volume = 3 * (1 / lamb)
#采样空间序列
x = np.arange(x_start,x_end,1/Fs_volume)

#t时间范围:0到19s
t_start,t_end = 0,19

#时间采样率设为信号频率的3倍
Fs_time = 3 * f
#采样时间序列
t = np.arange(t_start,t_end,1/Fs_time)

#空间采样点数
N = np.size(x)

#时间采样点数
M = np.size(t)

dataMatrix = np.zeros((M,N))
#注意举例子用的示例信号的w'和k'不要大于最大的频率w和波矢k
for index_row in range(0,M):
    for index_column in range(0,N):
        dataMatrix[index_row,index_column] = (A * np.sin(w * t[index_row] - k * x[index_column]) +
        A * np.sin(0.9*w * t[index_row] - 0.9*k * x[index_column]) +
        A * np.sin(0.8*w * t[index_row] - 0.8*k * x[index_column]) +
        A * np.sin(0.7*w * t[index_row] + 0.7*k * x[index_column]))
        
#绘图

#plt.rcParams['figure.figsize'] = (12,8)
#横轴为空间，纵轴为时间
#横轴为空间，纵轴为时间，注意时间是从上到下增加的
extent_x_t = [np.min(x),np.max(x),np.max(t),np.min(t)]
plt.subplot(2,1,1)
plt.xlabel('x (m)')
plt.ylabel('t(s)')
#参数origin : {‘upper’, ‘lower’}将数组的[0,0]索引放在轴的左上角或左下角,默认值‘upper’通常用于矩阵和图像
plt.imshow(dataMatrix,origin='upper',cmap='bwr',extent=extent_x_t)
#颜色代表的标量值
plt.colorbar(label='y=A*sin(w*t - k*x)')

plt.title('原始二维波形,A=24,f1=8,k1=3,f2=0.9f1,k2=0.9k1,f3=0.8f1,k3=0.8k1,f4=0.7f1,k4=-0.7k1')

如此构造的二维图像如下，它的横轴表示空间，纵轴表示时间：

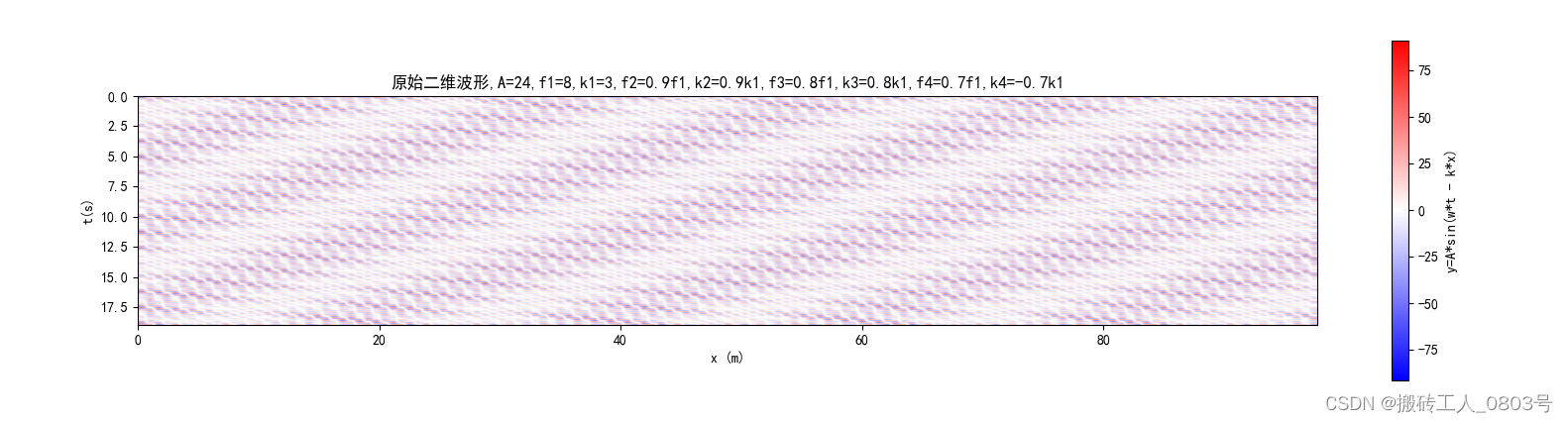
通过时间范围和时间采样率确定了在时间上采样得到M个点，通过空间范围和空间采样率确定了空间上采样得到的N个点，将采样得到的数值放在一个M行N列的矩阵中，当进行二维傅里叶变换后，那么矩阵的每一行的就表示一个频率点，而每一列就表示一个波矢点，而由该行列确定的位置点就存放该点进行二维傅里叶变换的结果值。使用二维傅里叶变换fft2()函数之后，要先将零频中心移动到输出矩阵的中心，即直接调用fftshift()函数即可，如此，输出矩阵的纵轴从上到下依次是正频率，0Hz，负频率；输出矩阵的横轴从左往右依次是负波矢，0，正波矢。之后同样的要去除M行N列输出矩阵中后一半行数的数据，即舍弃负频率的数据。
有了频率点和波矢点，只需按照前文的方法对这些频率点和波矢点进行一些运算即可获取对应的频率值和波矢值。即（$\tilde{A}(k,f)$）图中每一个点的横纵坐标就算出来了。
接着是计算（$\tilde{A}(k,f)$）图中每一个点的值，即傅里叶振幅$\tilde{A}$。M行N列的矩阵进行二维FFT之后，输出结果也是M行N列的矩阵，经过移频并舍弃负频率的数据之后，就变成了$\frac{M}{2}$行N列的矩阵，而且里面的每个元素都是复数。想当然的，必须先对该复数进行取模使之变成实数值。而下一步对这个$\frac{M}{2}$行N列的实数矩阵的处理就比较五花八门了，有对这个实数矩阵进行归一化处理的，也有进行取对数操作的。在下面给出的示例中就只进行取模，没有进一步处理。

#二维FFT
fft_Matrix = np.fft.fft2(dataMatrix)  
#将kx=0，f=0移动到输出矩阵的中心，并求复数的模
fft_Matrix = abs(np.fft.fftshift(fft_Matrix))
#对于频率部分，只取正频率，要舍弃矩阵一半的行数据
fft_Matrix = fft_Matrix[0:int(M/2),:]

####计算坐标轴####

#实空间转K空间，波长的倒数：波数，对比时间项wt和空间项-kx，可知得到的波数要乘以-1
wave_num = -1 * np.fft.fftfreq(N,1/Fs_volume)
#波数*2*pi等于波矢
kx = wave_num * (2 * np.pi)

#时间转频率
F = np.fft.fftfreq(M,1/Fs_time)
F = F[0:int(M/2)]

#保存数据：此处根据Origin软件绘制（等高线图-颜色填充）的方式给出两种保存矩阵数据的方式
#将横、纵坐标按照升序排列
kx.sort()
F.sort()
#方法一：保留矩阵的格式，直接把矩阵保存在文件中，横、纵坐标分别单独保存为文件
np.savetxt('FFTResult_2D_Matrix.txt', fft_Matrix,delimiter=' ')
print('二维FFT结果已写入FFTResult_2D_Matrix.txt，矩阵第一个值对应图像第一个像素点（左上角为坐标原点）的值，大小为：',fft_Matrix.shape)
np.savetxt('kx.txt', kx,delimiter=' ')
print('图像的横坐标即波矢（2*pi/lambda）已写入kx.txt')
np.savetxt('F.txt', F,delimiter=' ')
print('图像的纵坐标即频率已写入F.txt')

# #方法二：将色散矩阵fft_Matrix转换为包含3列数据（X,Y,颜色值）的TXT文件，它的行数为：色散矩阵行数*列数
# #转换方法：从色散矩阵左上角开始，即(F(max)，kx(min))，从左往右遍历列，从上往下遍历行，依次填充
# matrix_row,matrix_column = fft_Matrix.shape
# saveFileTotalRow = matrix_row * matrix_column
# saveFileMatrix = np.zeros((saveFileTotalRow,3))
# print('fft_Matrix.shape:',fft_Matrix.shape)
# print('saveFileMatrix.shape:',saveFileMatrix.shape)
# #一行行的填充saveFileMatrix
# for index_row in range(0,saveFileTotalRow):
    # #计算当前索引的行位置
    # index_F = int(index_row / matrix_column)
    # #计算当前索引的列位置
    # index_kx = index_row % matrix_column
    # #根据索引获取当前行的三个数值
    # #注意，频率值的索引是倒序排列的
    # value_F = F[int(matrix_row - 1 - index_F)]
    # value_kx = kx[index_kx]
    # value_Amplitude = fft_Matrix[index_F][index_kx]
    # #填充TXT文件中的一行
    # saveFileMatrix[index_row,0]=value_kx
    # saveFileMatrix[index_row,1]=value_F
    # saveFileMatrix[index_row,2]=value_Amplitude
    
# #列之间用空格分隔
# np.savetxt('dispersionResult_XYZ.txt', saveFileMatrix,delimiter=' ')
# print('色散图（XYZ）的数据已经写入dispersionResult_XYZ.txt，第一列为kx，第二列为F，第三列为该点的值')

#画图
#横轴为波矢，纵轴为频率（只取正频率）
extent_kx_F = [np.min(kx),np.max(kx),np.min(F),np.max(F)]
plt.subplot(2,1,2)
plt.xlabel('kx (m^-1)')
plt.ylabel('F(Hz)')
#参数origin : {‘upper’, ‘lower’}将数组的[0,0]索引放在轴的左上角或左下角,‘upper’通常用于矩阵和图像
plt.imshow(fft_Matrix,cmap='bwr',origin='lower',extent=extent_kx_F,aspect ='auto')
#颜色代表的标量值
plt.colorbar(label='|fft2(y)|')
plt.title('色散关系')
plt.show()

示例中使用了savetxt()将色散图的横坐标和纵坐标分别保存，然后将最终得到的实数矩阵保存下来。最后则是用颜色绘制函数绘制出矩阵中的每个位置的值映射到色条(colorbar)中的颜色，这样就得到了$\frac{M}{2}XN$个像素点的色散图。比如矩阵中第一行第一列的元素即第一个元素matrix[0,0]，它就应该绘制在色散图的左上角，即第一个像素。
将以上两段代码合并后运行，得到的输出图像如下所示：

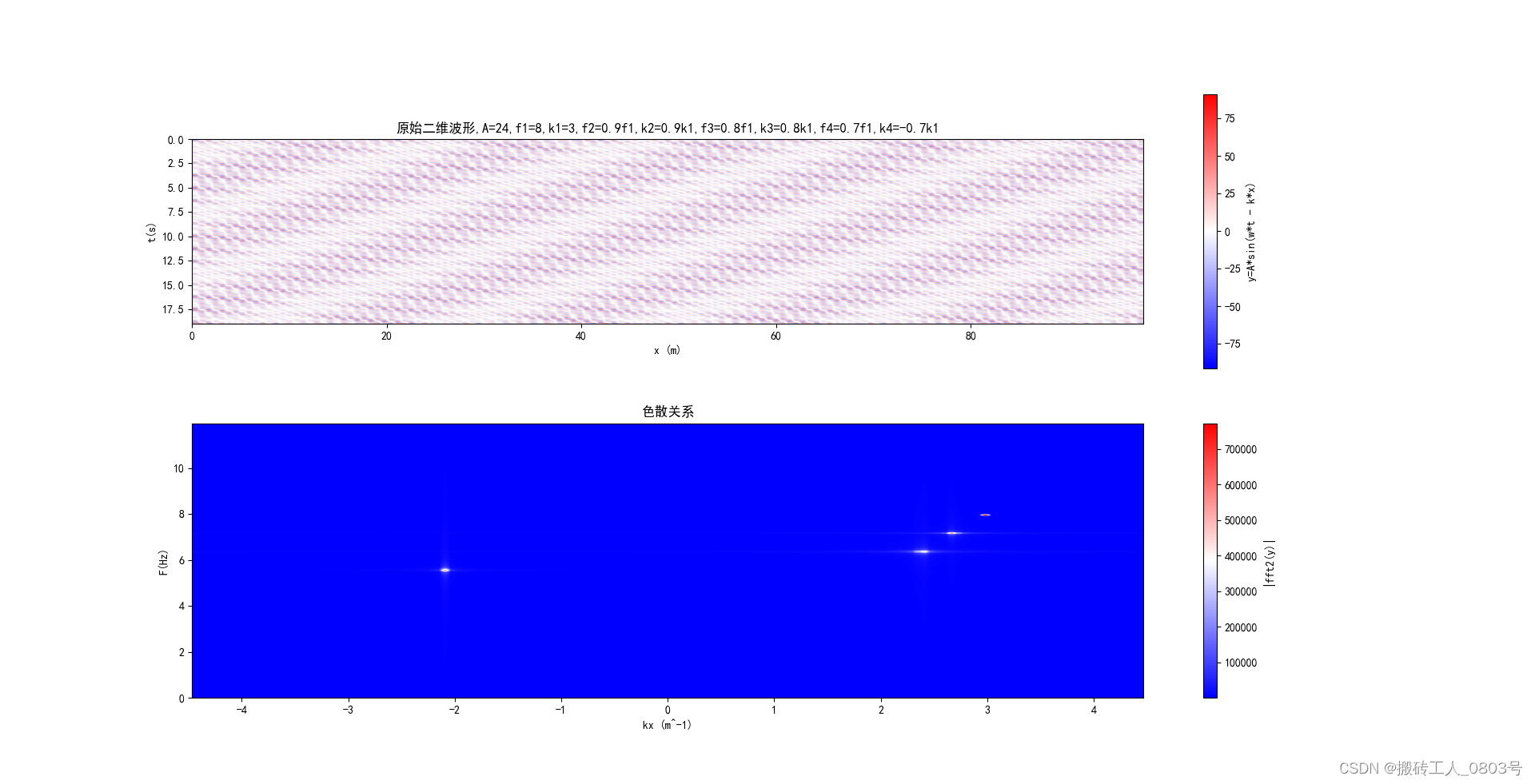
可以在色散图中找到组成原始图像的4个平面波的贡献情况：(频率,波矢)=(f,k)，(0.9f,0.9k)，(0.8f,0.8k)，(0.7f,-0.7k)。
以上内容便是适用于各个领域的傅里叶变换的通用基础技巧，接下来是介绍如何获取磁体系中传播的自旋波的频谱和色散关系，大家在阅读这部分的内容后，对于分析其他领域的时空波形来说可能启发一些相似的思路。

22/10/16 补充说明：

补充了将色散结果的矩阵保存下来的两种方式，方便使用Origin软件绘图。
方法一是直接保存矩阵的格式，但是在Origin中绘制这个矩阵时，图像横纵轴的坐标轴标签十分难搞定，所以不推荐使用该方式保存。
方法二是按照将图像中的每一个横、纵坐标点，和该点的颜色值的格式来保存，Origin绘图方式参考 学习…笔记08：Origin绘制常见图像的方法总结中的二.2节，这种方法没有坐标轴标签的困扰，是十分方便的，所以只推荐使用方法二！

#保存数据：此处根据Origin软件绘制（等高线图-颜色填充）的方式给出两种保存矩阵数据的方式
#将横、纵坐标按照升序排列
kx.sort()
F.sort()
#方法一：保留矩阵的格式，直接把矩阵保存在文件中，横、纵坐标分别单独保存为文件
np.savetxt('FFTResult_2D_Matrix.txt', fft_Matrix,delimiter=' ')
print('二维FFT结果已写入FFTResult_2D_Matrix.txt，矩阵第一个值对应图像第一个像素点（左上角为坐标原点）的值，大小为：',fft_Matrix.shape)
np.savetxt('kx.txt', kx,delimiter=' ')
print('图像的横坐标即波矢（2*pi/lambda）已写入kx.txt')
np.savetxt('F.txt', F,delimiter=' ')
print('图像的纵坐标即频率已写入F.txt')

# #方法二：将色散矩阵fft_Matrix转换为包含3列数据（X,Y,颜色值）的TXT文件，它的行数为：色散矩阵行数*列数
# #转换方法：从色散矩阵左上角开始，即(F(max)，kx(min))，从左往右遍历列，从上往下遍历行，依次填充
# matrix_row,matrix_column = fft_Matrix.shape
# saveFileTotalRow = matrix_row * matrix_column
# saveFileMatrix = np.zeros((saveFileTotalRow,3))
# print('fft_Matrix.shape:',fft_Matrix.shape)
# print('saveFileMatrix.shape:',saveFileMatrix.shape)
# #一行行的填充saveFileMatrix
# for index_row in range(0,saveFileTotalRow):
    # #计算当前索引的行位置
    # index_F = int(index_row / matrix_column)
    # #计算当前索引的列位置
    # index_kx = index_row % matrix_column
    # #根据索引获取当前行的三个数值
    # #注意，频率值的索引是倒序排列的
    # value_F = F[int(matrix_row - 1 - index_F)]
    # value_kx = kx[index_kx]
    # value_Amplitude = fft_Matrix[index_F][index_kx]
    # #填充TXT文件中的一行
    # saveFileMatrix[index_row,0]=value_kx
    # saveFileMatrix[index_row,1]=value_F
    # saveFileMatrix[index_row,2]=value_Amplitude
    
# #列之间用空格分隔
# np.savetxt('dispersionResult_XYZ.txt', saveFileMatrix,delimiter=' ')
# print('色散图（XYZ）的数据已经写入dispersionResult_XYZ.txt，第一列为kx，第二列为F，第三列为该点的值')

三、自旋波的频谱，色散

1.已有的自旋波分析程序

微磁模拟软件OOMMF和Mumax3都是使用OVF格式的文件来保存磁体系的磁化状态的，在进行频谱和色散分析之前，务必保证每个磁化文件之间的是按照相同间隔时间（即采样周期）来保存的。 比如模拟运行5ns，按照每5ps保存一次磁体系的磁化状态，那么模拟结束后会得到1000个磁化文件。对应到前文傅里叶变换中的参数，也就是时间采样周期Ts为5ps（时间采样频率Fs_time=1/Ts），时间采样点数M为1000。而空间采样周期（空间采样频率Fs_volume的倒数）呢？由于磁体系的空间分为x，y，z三个方向，所以就有三个方向上的空间采样周期，分别等于用户在模拟时在三个方向上设置的单元格尺寸。
用于分析自旋波频谱和色散关系的程序包有很多，比如在笔记03中提到过的MFA，又比如在笔记04中提到过的semargl3，其中MFA程序包是以Python源码的方式给出的，它要求磁化文件的数据格式是text文本格式，用户需要在代码里设置需要分析的参数，然后直接运行即可，由于有非常清晰的说明文档，所以MFA使用起来是非常简单的。而semargl3则是一个可执行程序，它要求磁化文件的数据格式是b8或者b4，而且要求每个磁化文件必须以.ovf作为后缀名，用户需要在semargl3的图形界面设置参数。它对自旋波的分析类型是我见过的程序包中最多的，不过它的说明文档不太详细，所以使用起来有一定的门槛。
此外，硕士论文《在磁畴壁中传播的自旋波束缚态的探测原理》的附录中给出了使用MATLAB获取自旋波的色散的代码，在OOMMF官方教程的最后几页PPT里面也有使用Python获取自旋波的色散的代码。
那么此处以MFA的源码为例，将解析它的内容（实际上就是加一点注释方便理解而已）来看一下怎么处理磁化文件来获取自旋波的相关信息。

2.频谱

（1）首先需要从所有磁化文件中导入三个磁化分量mx,my,mz中的一个磁化分量，该磁化分量是用于表征自旋波的振幅的。MFA采用多进程同时读取所有的磁化文件的某一磁化分量，返回得到了一个长度为文件数量的列表list(array[…],…)，列表的每一个元素是一个一维数组，数组中保存着该磁体系所有单元格的某一磁化分量：

#读取一个磁化文件中的某一磁化分量，name：文件名称；colum：读取的矢量分量
def fileload(name,colum):
    colum = int(colum)
    #磁化文件中'#'是注释
    m_oneFile = np.loadtxt(name, dtype = float,
                      comments = '#', usecols = (colum,))
    return m_oneFile

#该函数的返回值为[array([...]), array([...])...]，列表的一个元素表示保存一个磁化文件的某个分量的浮点型数组
#列表长度为当前文件夹中所有子文件数量
#dirc：存放磁化文件的目录
#start_stage，end_stage：需要的磁化文件的范围
#exportX,exportY,exportZ：选择磁化矢量的那个分量作为自旋波的振幅
#num：占用计算机核心的数量
def readUseMultiCore(dirc,start_stage,end_stage,exportX,exportY,exportZ,num):
    #磁化文件中的第三列表示Z分量
    if exportZ == 1:
        column = '2'
    #磁化文件中的第二列表示Y分量
    elif exportY == 1:
        column = '1'
    #磁化文件中的第一列表示X分量
    else:
        column = '0'

    #定义一个保存磁化文件名称的空列表
    files = []
    #walk函数会以文件夹为单位自顶而下遍历指定文件目录，
    #返回的三个参数分别表示当前文件夹, 当前文件夹中的子文件夹, 当前文件夹中的子文件
    for i,j,k in os.walk(dirc):
        #获取当前文件夹中所有磁化文件，并保存到列表中
        #因此，这里的files是二维列表：files[k[...]]
        files.append(k)
    #将files转化为一维列表
    files = files[0]
    #对列表中的磁化文件进行按名称升序排序
    files.sort()
    files_sort = files[:]
    #创建一个保存磁化文件全路径名称的列表
    files_new = []
    for i in range(start_stage,end_stage):
        files_new.append(dirc+ '/' + files_sort[i])   
    if num == 0:
        #没有指定核心数量时，表示使用所有cpu核心
        pool = Pool()
        #将需要扩展的的原始函数作为partial函数的第一个参数，原始函数的一系列参数作为partial的后续参数，最后生成一个带默认参数的新函数
        #接着pool.map会把新函数（第一个参数）和新函数的一系列参数（第二个参数即列表）映射到多进程池中运行
        #此处表示，返回读取所有磁化文件中的指定磁化分量的值
        m_allFiles = pool.map(partial(fileload,colum=column),files_new)
        #关闭进程池
        pool.close()
        #主进程阻塞等待子进程的退出，join方法要在close或terminate之后使用
        pool.join()
    else:
        pool = Pool(processes = num)
        m_allFiles = pool.map(partial(fileload,colum=column),files_new)
        pool.close()
        pool.join()
    return m_allFiles

（2）接着是对每一个磁化文件中的指定区域进行处理，从磁体系所有单元格中找到用户指定区域范围内的单元格，并对这些单元格重新排序使之成为一个一维的单元格链。

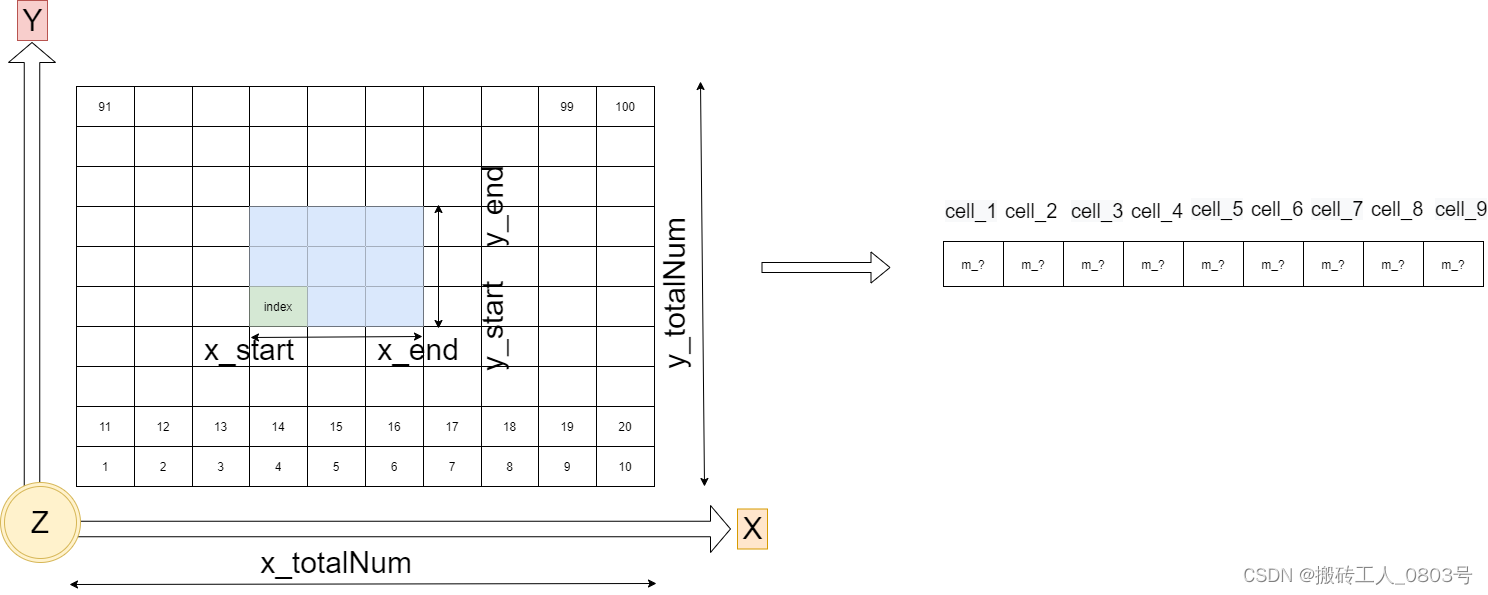
比如第一个磁化文件中的指定空间范围：x_start到x_end，y_start到y_end，z_start到z_end，那么根据三个方向上的单元格尺寸就可以得到指定区域左下角的第一个单元格的索引index，然后按照先x方向，后y方向，最后z方向找到指定区域的单元格，并把这些单元格中重新存储到一个一维链中得到cell_1,cell_2…。如此操作结束后，将这对第一个磁化文件处理后得到的单元格链放入新矩阵的第一行，然后对剩余的磁化文件也是如此处理，将得到的每一个单元格链依照保存的时间顺序放在新矩阵的每一行。最终得到的新矩阵的形状是M行N列的，行表示时间采样点，列表示空间采样点。

#将正在遍历的磁化文件中的磁化矢量的某个分量装载到特定格式的矩阵中
#x_num,y_num,z_num：指定区域包含的三个坐标方向上的单元格数量
#x_cellSize,y_cellSize,z_cellSize：xyz三个坐标方向上的单元格的尺寸
#x_start,y_start,z_start：用户指定区域的开始坐标
#x_totalNum,y_totalNum：整个磁体系的x和y方向上的单元格数量
#M_matrix：行数为文件数量，列数为指定区域包含的总单元格数量，元素的值为零
#file：保存着一个矢量场文件的某个分量的数组
#i：正在遍历的矢量场文件的索引
def loadDataToMatrix(x_num,y_num,z_num,x_cellSize,y_cellSize,z_cellSize,
           x_start,y_start,z_start,x_totalNum,y_totalNum,M_matrix,file,i):
    for z_index in range(0,z_num):
        for y_index in range(0,y_num):
            for x_index in range(0,x_num):
                #待填充的矩阵的索引，按照一维展开的方式来排序
                indexOfMatrix = int(z_index * (x_num * y_num) + y_index * x_num + x_index)
                #指定区域的单元格的索引，从左下角开始
                indexOfSelectedRegion = (int(x_start / x_cellSize) + x_index) + ((int(y_start / y_cellSize) + y_index) * x_totalNum) + (
                (int(z_start / z_cellSize) + z_index) * (x_totalNum * y_totalNum))
                #填充时间点（行）单元格（列）矩阵
                M_matrix[i,indexOfMatrix] = file[indexOfSelectedRegion]
    return M_matrix

def GetDocs(m_allFiles,start_stage,end_stage,x_totalSize,y_totalSize,z_totalSize,x_start,y_start,z_start,
            x_end,y_end,z_end,x_cellSize,y_cellSize,z_cellSize,
            exportX,exportY,exportZ):
    #整个磁体系的x和y方向上的单元格数量
    x_totalNum,y_totalNum = int(np.round(x_totalSize / x_cellSize)), int(np.round(y_totalSize / y_cellSize))
    #指定区域包含的三个坐标方向上的单元格数量
    x_num = int(np.round((x_end - x_start) / x_cellSize))
    y_num = int(np.round((y_end - y_start) / y_cellSize))
    z_num = int(np.round((z_end - z_start) / z_cellSize))
    #指定的文件范围和指定区域包含的总单元格数量
    selectedFlieNum = end_stage - start_stage + 1
    selectedCellNum = x_num * y_num * z_num
    if exportX == 1:
        #np.zeros((m,n))返回一个m行，n列，用0填充的矩阵
        Mx_matrix = np.zeros((selectedFlieNum,selectedCellNum))
    else:
        Mx_matrix = 0
    
    if exportY == 1:
        My_matrix = np.zeros((selectedFlieNum,selectedCellNum))
    else:
        My_matrix = 0
    
    if exportZ == 1:
        Mz_matrix = np.zeros((selectedFlieNum,selectedCellNum))
    else:
        Mz_matrix = 0
    
    #读取到的磁化文件的数量
    flieNum = len(m_allFiles)
    # 读取指定区域单元格的磁化分量
    if exportZ == 1:
        for i in range(0,flieNum):
            file = m_allFiles[i]
            Mz_matrix = loadDataToMatrix(x_num,y_num,z_num,x_cellSize,y_cellSize,z_cellSize,
            x_start,y_start,z_start,x_totalNum,y_totalNum,Mz_matrix,file,i)
    else:
        Mz_matrix = Mz_matrix
    
    if exportY == 1:
        for i in range(0,flieNum):
            file = m_allFiles[i]
            My_matrix = loadDataToMatrix(x_num,y_num,z_num,x_cellSize,y_cellSize,z_cellSize,
            x_start,y_start,z_start,x_totalNum,y_totalNum,My_matrix,file,i)
    else:
        My_matrix = My_matrix
    
    if exportX == 1:
        for i in range(0,flieNum):
            file = m_allFiles[i]
            Mx_matrix = loadDataToMatrix(x_num,y_num,z_num,x_cellSize,y_cellSize,z_cellSize,
            x_start,y_start,z_start,x_totalNum,y_totalNum,Mx_matrix,file,i)
    else:
        Mx_matrix = Mx_matrix
    
    print('所有磁化文件的磁化分量值已读取到行（时间）列（单元格）的矩阵中')
    return Mx_matrix, My_matrix, Mz_matrix

这一部分代码的难点在于用户要对OVF格式的矢量文件要有一个深入的了解，默认情况下空间坐标原点在磁体系的左下角，指定区域的范围是：x_start，y_start，z_start，x_end，y_end，z_end，那么该区域在三个方向上的单元格数量分别为：x_num，y_num，z_num，指定区域的左下角的第一个单元格索引为x_start除以x_cellSize，对于指定区域每一行的单元格，索引值就用一个范围为x_num的for循环进行遍历即可得到该行内的单元格，而对于指定区域的y方向的单元格索引，相应的用一个范围为y_num的for循环进行遍历即可，且在y方向每增加一次，则应该跳过磁体系在x方向的所有单元格，z方向同理，z方向每增加一次，则应该跳过磁体系在xy平面的所有单元格。

（3）计算频谱：通过前文的描述，我们需要固定空间为一个点（此处最小的空间点就是一个单元格），得到该点关于时间变化的磁化分量。但是此处用户的指定区域有N个单元格，即N个空间采样点，该如何压缩使之成为一个点呢？
可能有人马上想到了，在同一个时间采样点上，直接把N个点的磁化分量加起来，然后除以N，即取用户指定区域所有单元格的平均磁化分量，如此即可把M行N列矩阵压缩为M行1列的形状了。然后直接对这个一维序列进行一维傅里叶变换，得到的频谱即为最终结果。
可能还有人想到另一种方法，即先对指定区域的每一个单元格进行一维傅里叶变换（即矩阵的列方向为傅里叶变换的方向），结果仍是一个M行N列的矩阵，之后在对指定区域的所有单元格取傅里叶振幅的平均值，将这个平均频谱作为最终结果。
以上方法都是可行的！参考文献《Micromagnetic Simulations in Magnonics》（DOI:10.1007/978-3-642-30247-3_8），文中描述了三种处理多个单元格频谱的方法：

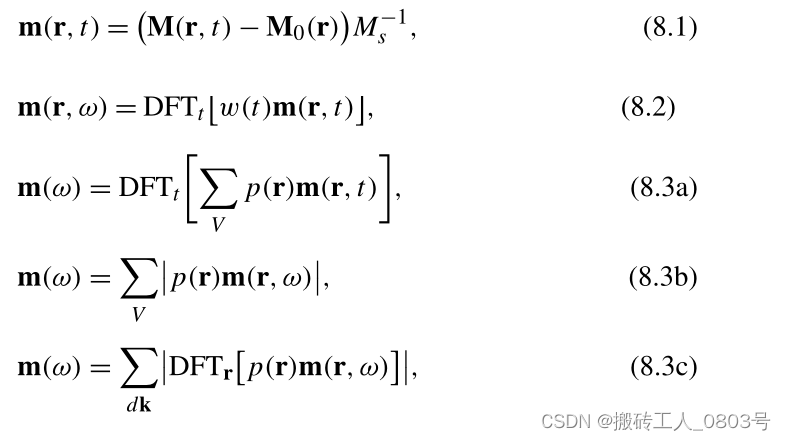
(8.1)表示将从所有磁化文件中减去基态磁化状态，并除以饱和磁化强度来实现将要分析的磁化分量进行归一化。
(8.3a)对应在每一个时间点上，先把空间上所有单元格的磁化分量平均为一个单元格的磁化分量，然后对这个单元格的所有时间点上的磁化分量进行一维傅里叶变换，然后就可以得到频谱图了。
(8.3b)表示先对每一个单元格在所有时间点上进行一维傅里叶变换，接着对所有单元格的傅里叶变换结果取平均值，如此也得到了一个频谱图。
(8.3c)则表示对在所有时间点上对所有单元格进行二维傅里叶变换，然后可以选择特定波矢区域的单元格的频谱图。

在这篇参考文献中，比较了这三种方法的结果差异如下：

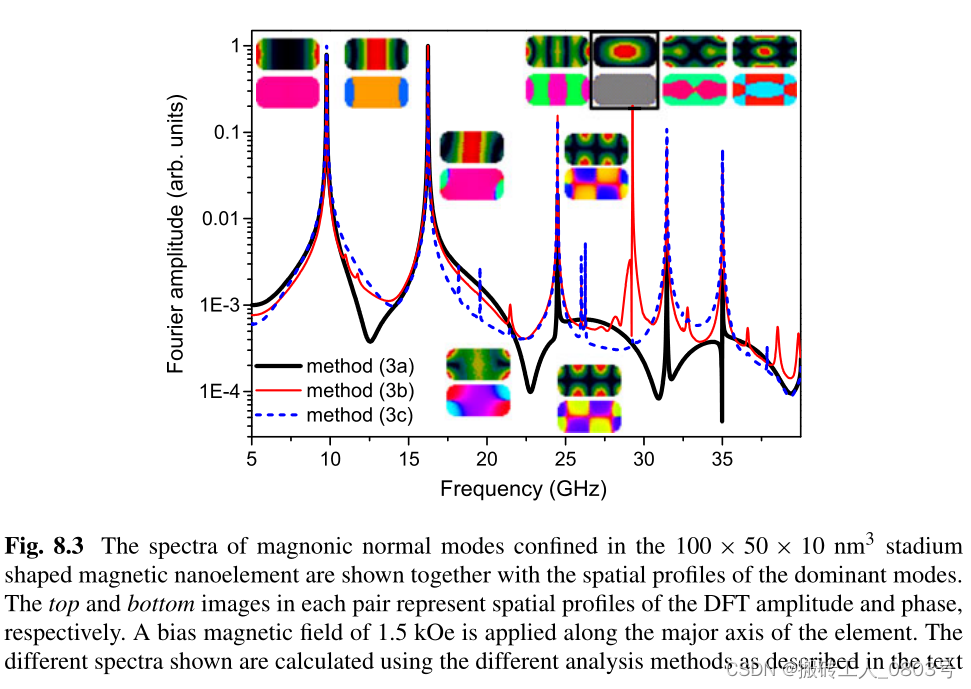
对于(8.3a)，由于是先在空间上取平均，它会降低空间中非均匀模式的自旋波的频率贡献。从图中可以看到，相比(8.3b)和(8.3c)，它的频谱曲线没有太多的峰，也没有丰富的频谱细节。
(8.3b)和(8.3c)则是先对空间中的所有点求出频谱，如此便不会降低空间中非均匀模式的自旋波的频率贡献，因此可以得到任何模式的自旋波的的频谱，但是正如参考文献中所说的，由于数值模拟的误差和采样原因，可能会出现一些人为的假谱线。

从MFA的源码中可以看到，MFA采用的方法是(8.3b)，即先对指定区域中的所有单元格求出频谱，然后再取该区域中的平均频谱。

#对矩阵（行代表时间，列代表空间单元格）进行一维傅里叶变换
#Mx,My,Mz：三者之一保存着待分析的矩阵
#export_x,export_y,export_z：待分析的磁化分量
#T:采样周期
#f_min，f_max：设置最终频谱图的频率上下限
def matrixFFT(Mx,My,Mz,export_x,export_y,export_z,T,f_min,f_max):
    if export_z == 1:
        M_matrix = Mz
    elif export_y == 1:
        M_matrix = My
    else:
        M_matrix = Mx
    
    #得到M_matrix的行(M)和列(N)数，
    #行是采样时间间隔:t0,t1,t2...tM-1，列是指定区域单元格数量cell0,cell1...cellN-1
    M,N = M_matrix.shape
    #时间采样频率
    Fs_time = 1 / T
    #将采样点等间隔分为序列号：0,1,2...M-1
    n = np.linspace(0,M-1,M)
    #根据每个序列号获取对应的频率值（即横轴坐标），频率分辨率为采样频率/采样点数
    fn = Fs_time / M * n
    #N个实数点进行FFT之后也有N个复数点，这里需要对每个单元格进行FFT，所以结果点数为N*M
    fftMatrix = np.zeros((N,M))
    #在时间（M行）-单元格（N列）矩阵中，按照列的方向来求每个单元格的FFT
    for i in range(0,N):
        #将FFT得到的M*N个数据点按照N行（表示单元格），M列（表示时间）来存放在fftMatrix中
        fftMatrix[i,:] = np.abs(np.fft.fft(M_matrix[:,i]))
        #对FFT后的复数结果的模值进行处理，得到正确的幅值:
        #除了第一个点（0Hz）外，对模值要先除以采样点数量，再乘以2
        fftMatrix[i,:] = fftMatrix[i,:] / M * 2
        #对于第一个点（0Hz），只需对模值除以采样点数量即可
        fftMatrix[i,0] = fftMatrix[i,0] / 2
    
    #对于每个频率点来说，对应的幅值是对所有单元格在该频率点下的幅值取平均值
    aveMatrix = np.zeros((1,M))
    #axis为0（1）表示对矩阵的每一列（行）取均值
    #对每一列的所有单元格求平均值，返回 1*M列的矩阵
    aveMatrix[0,:] = np.mean(fftMatrix[:,0:M], axis = 0,keepdims = True)
    
    #只取前一半部分正的频率点，舍弃后一半部分负的频率点
    F = fn[range(int(M / 2))]
    aveMatrix = aveMatrix[0,range(int(M / 2))]
    
    #归一化幅度
    aveMatrix = aveMatrix / np.max(aveMatrix)
    #将结果保存到文件
    FFTResult_time = np.zeros((len(aveMatrix),2))
    #第一列为频率
    FFTResult_time[:,0] = F
    #第二列为振幅
    FFTResult_time[:,1] = aveMatrix
    #列之间用空格分隔
    np.savetxt('FFTResult_time.txt', FFTResult_time,delimiter=' ')
    print('FFT结果已经写入FFTResult_time.txt，第一列为频率，第二列为振幅')
    
    #####绘图#####
    #变换横坐标（HZ->GHz）
    F = F / 1e9
    #矩阵.T返回矩阵的转置矩阵
    plt.plot(F,aveMatrix.T,linewidth = 2)
    plt.xticks(fontsize=18)
    plt.yticks(fontsize=18)
    plt.xlabel(r'$mathrm{Frequencyenspace (GHz)}$',fontsize=18)
    plt.ylabel(r'$mathrm{Normalizedenspace FFTenspace powerenspace (arb.units)}$',fontsize=18)
    #频谱图中显示的频率上下限
    plt.xlim((f_min,f_max))
    plt.show()
    return;

该部分代码没有任何难点，有了前文的铺垫，是很容易理解的。

3.色散

在计算色散时，需要的是x，y，z三个空间方向中的一个。在计算自旋波的频谱时，我们得到了用于一维FFT的M行N列的输入矩阵，其中N是三个方向总的单元格数量，所以需要将它压缩到一个方向。MFA源码中为x方向，具体处理方式为：将三个方向总的单元格数量（x_num X y_num X z_num）压缩到待分析的波矢的方向的单元格数量（x_num），即对y方向和z方向的单元格中的磁化分量取平均值。如此，M行N列矩阵变成了M行x_num列的矩阵。
对这个M行x_num列的矩阵进行二维傅里叶变换，之后也得到了一个M行x_num列的输出矩阵，而且输出矩阵中的每个元素都是复数。接着要将零频(f=0，k=0)移动到输出矩阵的中心，即直接调用fftshift()函数，然后和前文一样，舍弃输出矩阵中一半的行数据（负频率），于是输出矩阵变成了$\frac{M}{2}$行x_num列了。之后还要对这个$\frac{M}{2}$行x_num列的矩阵取模，归一化，取对数等操作。

#对矩阵（行代表时间，列代表空间单元格）进行二维傅里叶变换
#Mx,My,Mz：三者之一保存着待分析的矩阵
#export_x,export_y,export_z：选择作为自旋波的振幅的磁化分量
#Ts,Vs：时间采样周期和空间采样周期（即波矢方向的单元格尺寸）
#T_resample,X_resample：是否对时间和空间重采样
#win,Resample_Switch：是否加窗，重采样
#f_cutoff,klim_cutoff：截止频率和截止波矢
#x_start,x_end：x方向的开始和结束坐标，确定了波矢为x方向
#x_cellSize：单元格x方向的尺寸

def matrixFFT2(Mx,My,Mz,export_x,export_y,export_z,Ts,Vs,
          T_resample,X_resample,win,Resample_Switch,
          f_cutoff,klim_cutoff,x_start,x_end,x_cellSize):
    if export_z == 1:
        M0_matrix = Mz
    elif export_y == 1:
        M0_matrix = My
    else:
        M0_matrix = Mx
    #M为时间，n为指定区域的总单元格（x*y*z方向）
    M, n = M0_matrix.shape
    #指定区域的x方向包含多少个单元格
    N = int((x_end - x_start) / x_cellSize)
    M_matrix = np.zeros((M,N))
    #只需要x方向（波矢方向）的单元格，即对波矢的垂直方向的单元格求平均
    start = 0
    end = N
    count = 0
    while end <= n:
        M_matrix = M_matrix + M0_matrix[:,start:end]
        start += N
        end += N
        count += 1
    M_matrix = M_matrix / count

    ###重采样和加窗###
    #对原始矩阵进行重采样后，矩阵的形状会改变
    M_fft, N_fft = M, N
    #定义一个新矩阵来保存对原始矩阵进行重采样后的结果
    Matrix = np.zeros((M_fft,N_fft))
    
    #重采样
    if Resample_Switch == 1:
        #对原始矩阵进行重采样后，矩阵的形状会改变
        M_fft, N_fft = round(M / T_resample), round(N / X_resample)
        j = 0
        for i in range(0,N-1):
            if np.mod(i,X_resample) == 0:
                Matrix[:,j] = M_matrix[:,i]
                j += 1
    else:
        Matrix = M_matrix
    
    #加窗
    if win == 1:
        from scipy.signal import chebwin as chebwin
        attenuation = 50.0
        win1 = chebwin(M_fft,attenuation)
        win2 = chebwin(N_fft,attenuation)
        win1 = win1[np.newaxis,:]
        win2 = win2[np.newaxis,:]
        win1 = win1.T
        win = np.dot(win1, win2)
        Matrix = Matrix * win
    else:
        win = win
    
    #二维傅里叶变换
    fftMatrix = np.zeros((M_fft,N_fft))
    fftMatrix = np.fft.fft2(Matrix)
    #移频之后取模值
    fftMatrix = np.abs(np.fft.fftshift(fftMatrix))

    #(1 / Ts)为时间采样频率，频率分为两半，并把单位转化为GHz
    F = (1 / Ts) / 2 / 1e9
    #(1 / Vs)为空间采样频率，波矢分为两半，并把单位转化为nm^-1（计算之后为负值）
    kx = (1 / Vs) / 2 / 1e9 * (-2 * np.pi)
    
    #fftMatrix的行是时间->频率（只选取正频率），列是空间->波矢（选取所有点）
    fftMatrix = fftMatrix[0:round(M_fft/2), 0:N_fft-1]
    #对FFT结果模值的归一化取分贝值
    fftMatrix = 10 * np.log10(fftMatrix / np.max(fftMatrix))

    #根据矩阵中所有元素获得一个平均值
    M_mean = np.mean(fftMatrix)
    #获取矩阵中最大值
    M_max = np.max(fftMatrix)
    
    #clip(a, a_min, a_max, out=None, **kwargs)：将矩阵a中的值限制在最小值和最大值之内
    fftMatrix = np.clip(fftMatrix,M_mean,M_max)
    
    #画图
    #图像横向方向的放大因子
    multi_horizontal = 2e2
    X_neglim, X_poslim = kx * multi_horizontal, -kx * multi_horizontal    #在横轴方向放大图像
    Y_neglim, Y_poslim = 0, F
    extent = [X_neglim,X_poslim,Y_neglim,Y_poslim]
    plt.figure()
    plt.rcParams['figure.figsize'] = (9.0,8.5)
    #参数：origin : {‘upper’, ‘lower’}将数组的[0,0]索引放在轴的左上角或左下角。‘upper’通常用于矩阵和图像。
    #cmap = plt.cm.jet将标量数据映射到色彩图：蓝-青-黄-红
    #extent：(left, right, bottom, top）数据坐标中左下角和右上角的位置。 如果为“无”，则定位图像使得像素中心落在基于零的（行，列）索引上。
    plt.imshow(fftMatrix, cmap = plt.cm.jet, origin='upper',extent=extent)
    
    #在横轴方向放大图像
    klim_cutoff = klim_cutoff * multi_horizontal
    if klim_cutoff in [20, 40, 60, 80, 100, 120, 140, 160, 180, 200]:
        plt.xticks([-200,-180, -160,-140,-120,-100,-80,-60,-40,-20,
            0,20,40,60,80,100,120,140,160,180,200],
            ['-1.0','-0.9','-0.8','-0.7','-0.6','-0.5','-0.4','-0.3','-0.2','-0.1',
            '0','0.1','0.2','0.3','0.4','0.5','0.6','0.7','0.8','0.9','1.0'],fontsize = 18)
    elif klim_cutoff in [2, 6, 10, 14, 18]:
        plt.xticks([-18,-14,-10,-6,-2,0,2,6,10,14,18],
            ['-0.09','-0.07', '-0.05','0.03','0.01', 
            '0','0.01', '0.03', '0.05','0.07','0.09'],fontsize = 18)
    else:
        plt.xticks([-16,-12,-8,-4,0,4,8,12,16],
           ['-0.08', '-0.06', '-0.04','-0.02','0','0.02', '0.04', '0.06','0.08'],fontsize = 18)
    plt.yticks(fontsize = 18)
    plt.xlim(-klim_cutoff,klim_cutoff)
    plt.ylim(0,f_cutoff)
    #将色条减少为图形高度的一半
    plt.colorbar(shrink = 0.5)
    plt.xlabel(r"$mathrm{Waveenspace vector}enspace k_xenspace mathrm{(nm^{-1})}$",
               fontsize = 17)
    plt.ylabel(r'$mathrm{Frequencyenspace (GHz)}$',fontsize = 17)
    plt.savefig('Dispersion curve.eps', dpi=500)
    plt.show()
    return fftMatrix

最后绘制这个$\frac{M}{2}$行x_num列的矩阵的图像时进行了额外的处理，即关于坐标轴的刻度标注问题：
①纵轴直接按照从小到大的顺序标注即可，不过需要注意，纵轴的起始点为0Hz。
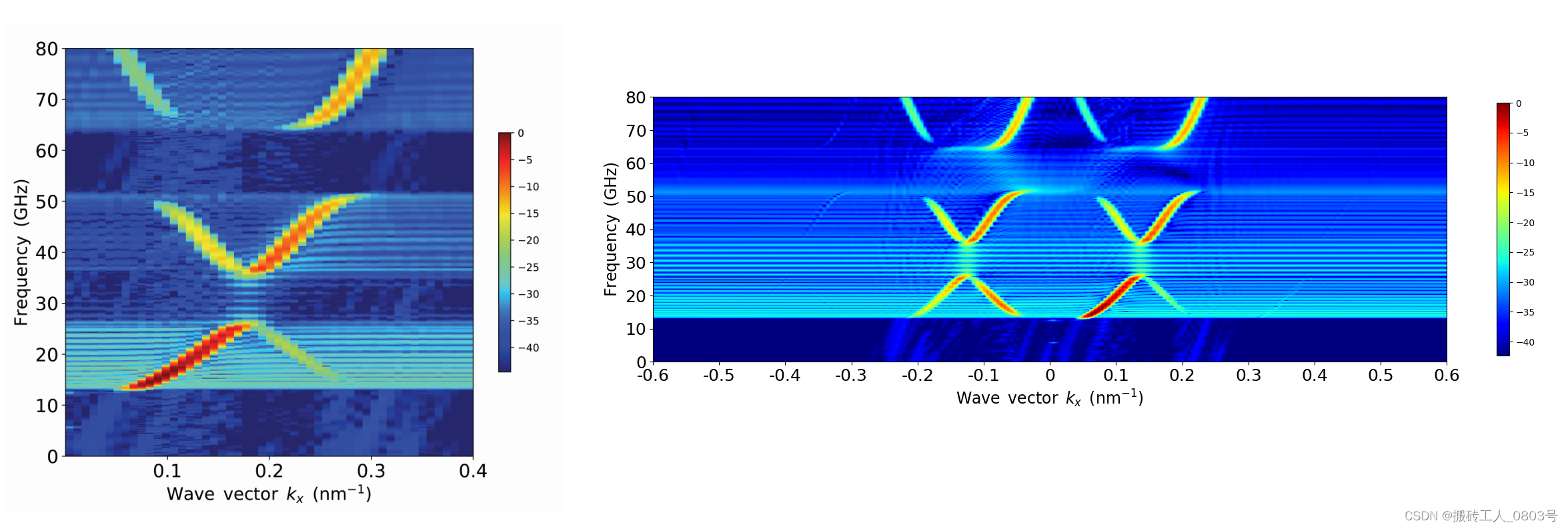
②横轴则是进行放大处理，此处就是将色散图在横向方向上放大了2e2倍。而且相比于MFA原来只显示正波矢的的限制，此处则取消了这个限制，运行MFA自带的示例，对比取消波矢限制的前（左图）后（右图）如下：

后记

最后

以上就是魁梧铅笔为你收集整理的学习...笔记05：时间，空间，时空傅里叶变换的基本技巧、获取自旋波的频谱图和色散图前言一、傅里叶变换的作用二、时间、空间、时空的傅里叶变换三、自旋波的频谱，色散后记的全部内容，希望文章能够帮你解决学习...笔记05：时间，空间，时空傅里叶变换的基本技巧、获取自旋波的频谱图和色散图前言一、傅里叶变换的作用二、时间、空间、时空的傅里叶变换三、自旋波的频谱，色散后记所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。