Note: 以下分析内容很可能是错误的,仅供参考,可以直接查看结论,结论会比较靠谱一点
目前搜集到的截位的方法有下面几种
负数直接截位后+1
Truncate:直接截位
Rounding:舍入截位
如果将截位截掉的部分看做小数部分,截掉之后剩下的部分看做整数部分的话,我们可以得到如下表的对应关系。
| +1.2 | -1.2 | +1.5 | -1.5 | +1.7 | -1.7 | +2.0 | -2.0 | ||
|---|---|---|---|---|---|---|---|---|---|
| 负数截位后加1 | +1 | -1 | +1 | -1 | +1 | -1 | +2 | -1 | 所有数都按绝对值取floor |
| Truncate | +1 | -2 | +1 | -2 | +1 | -2 | +2 | -2 | 正数取floor,负数按绝对值取ceil |
| Rounding | +1 | -1 | +2 | -2 | +2 | -2 | +2 | -2 | 所有数按绝对值取四舍五入 |
如对16位的0000 0000 0001 1000直接截掉后4位得到1,可将0000 0000 0001看做整数,1000看做小数,4bit位宽的取值范围为0 ~ 15,则本次截掉的数为8/16 = 0.5。如果按照四舍五入的方式的话,后4个bit是0 ~ 7就舍掉,8 ~ 15就截掉之后整数部分+1,这里因为截掉的部分为8,所以整数部分需要加1,最终结果为2,这就是Rounding。
1. 绝对值误差分析
这个分析基于的原理是,对于一个模值 ∣ X ∣ |X| ∣X∣,对 ± ∣ X ∣ ±|X| ±∣X∣进行同样位宽的截位后得到的两个模值应当是相同的。分析的过程如下:
- 生成位宽为16长度为N的一个整数数组 DEC
- 对这个DEC中的每一个数据取相反数得到converse_DEC = - DEC
- 分别对DEC和converse_DEC进行直接截位得到truncate_DEC和converse_truncate_DEC
- 计算error_rate = sum(abs(truncate_DEC+converse_truncate_DEC))/N
- 循环3、4步获得截位位宽1 ~ 15的error_rate
- 重复3、4、5步得到负数截位后加1和Rounding的结果
得到的结果如下图所示,可以看到随着截位位宽的增加,Truncate的误差概率接近于1,负数截位后加1的误差概率接近于0。而Rounding的误差概率一直都为0.
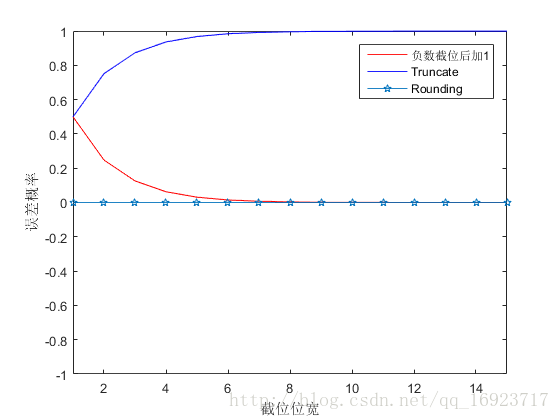
在截掉的部分为0时,负数截位后加1和Truncate会出现特殊情况,如表中的±2.0。此时Truncate的精度与Rounding一样,而负数截位后加1的方式出现了偏差。这是因为负数的二进制补码的特殊性引起的,在截掉的部分不全为0的情况下,直接截位时会将二进制补码转换时加的1截掉,而当截掉的部分全为0时,这个1因为进位而进入到了高位,直接截位不会将其删除。所以才出现了图中那个奇怪的现象,因为只有当截掉的部分全部为0时,Truncate得到的两个模值才会相等,而负数截位加1的两个模值也只有在这个时候才会不等。N个bit出现全为0的概率是 p = 1 2 N p = frac{1}{2^N} p=2N1,所以如果画出下面两个曲线的话,它们是会跟前两种截位方式的曲线完全重合的。
plot(2.^(-(1: 15))), hold on
plot(1 - 2.^(-(1: 15)))
为了对比,将它们统一减去一个1,得到下图
plot(2.^(-(1: 15)) - 1), hold on
plot(1 - 2.^(-(1: 15)) - 1)
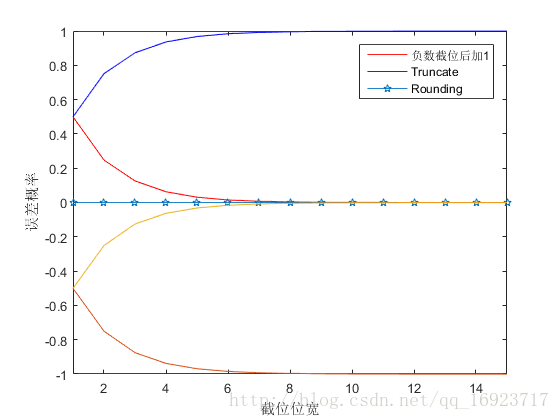
从上面分析结果来看,负数截位加1的方式在截位位宽大于8位后,其误差就接近0了,而Rounding方式更夸张,不管截多少位,误差都是0. 但事实上,上面分析的误差的参考值的选取是不对的,它忽略了信号是一个整体的事实,各采样点之间是相互关联的。所以这个分析基本上是没有什么意义的,把它贴上来的原因是这个分析花了好长时间,不贴上来对不起辛勤的劳动,而且也可以作为反面参考教材,也是有意义的吧??

2. 线性缩放分析
这个分析基于的原理是,认为理想的截位是信号整体的缩小和放大,而实际截位时具体到每一个采样点上的缩放倍数是不一致的,所以基于这一点进行了下面的误差分析。
- 随机产生 1 0 5 10^{5} 105个位宽为16 的有符号整数 x,x ≠ 0
- 用三种方式截掉低4位得到 y,(截掉低4位相当于x除以16)
- 得到 z = y ÷ x
- 得到 d = abs(z - 1 16 frac{1}{16} 161)
-
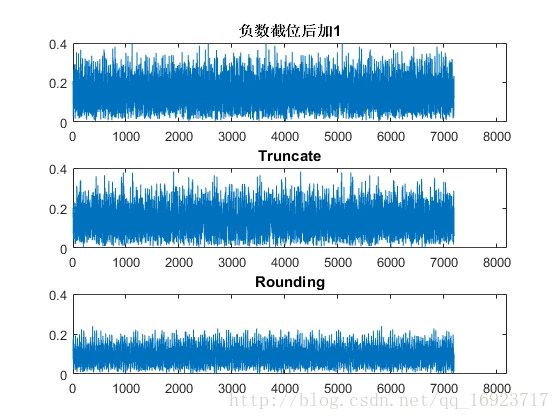
分析z的频谱如图所示,可以看到Truncate和负数截位后加1两种方式的高频部分的功率都超过了0.2,而Rounding的明显低于0.2,说明Rounding的效果是最好的。注意这里低频是没有画出来的,因为z基本上还是在 1 16 frac{1}{16} 161附近波动,所以低频信号功率很大,且三种方式基本一致。
-
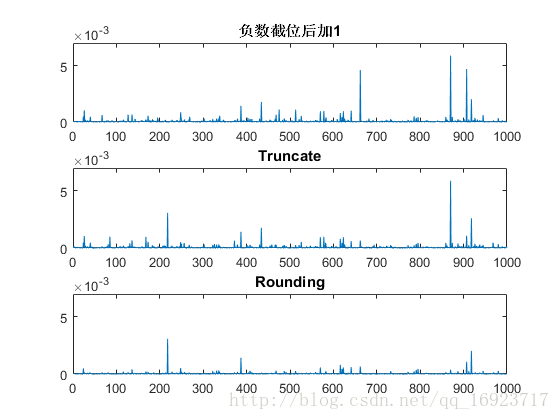
plot(d)如图所示,可以看到Rounding的波动最小,与真实倍数 1 16 frac{1}{16} 161差别最小,而负数截位后加1和Truncate的结果还是基本一致。
- 取前1000个数据
_
_ - 取前10000个数据
_
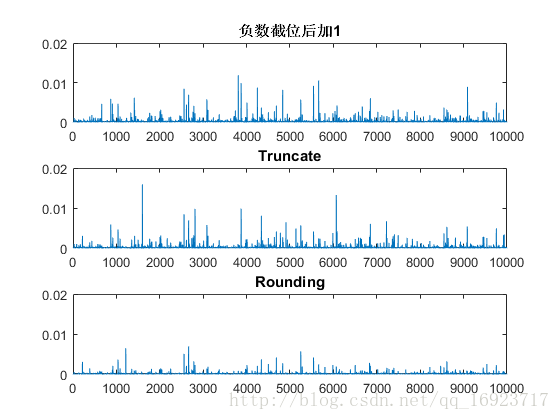
_ - 取前100000个数据
_
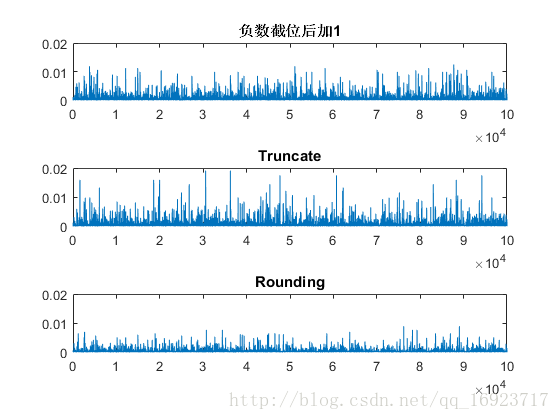
注意:在plot之前去掉了一些不具参考价值的结果,如对0000 0000 0000 1000截位后的结果为0或者1,得到的倍数结果就是0或者 1 8 frac{1}{8} 81,与 1 16 frac{1}{16} 161相差太远,不利于分析其他结果。
3. 总结
其实上面都是我胡乱分析的,分析的方法本身可能就是错误的。
不过,经过这些折腾还是得到了一个有用的结论:
一般情况下我们对信号进行直接截位(Truncate)就行了,如果对截位精度要求较高,则采用舍入截位(Rounding)方式,如果还不够(不是特殊领域的话应该都够了吧??),那么可能就要研究一下Dither方法了。**不建议采用负数截位后+1的方式,**因为有可能该方式的精度与Truncate是一样的,并且即使是它的精度介于Truncate和Rounding之间,使用它也不如使用Rounding,因为Rounding消耗的资源和代码量也仅仅比它多一点点,并且在对精度要求很高的应用中,FPGA的规模应当也是相当大的,这一点点资源是可以忽略不计的。而且Xilinx和Altera的数字信号处理的部分IP核中也只提供了Truncate和Rounding的选项。
《数字信号处理过程中信号截位误差抑制方法研究》-- 郭连平 田书林 王志刚
这篇论文里研究了Dither方法的性能,也可查看其参考文献
另外舍入截位有个更方便的实现方法,如截N位的过程:
- 判断数据的符号,正或负;
- 正数 + 2 N − 1 2^{N - 1} 2N−1
- 负数 + 2 N − 1 − 1 2^{N - 1} - 1 2N−1−1
- 截掉N位
这种方法其实是利用了补码截位时正数取floor,负数取cell的特性,上面的操作过程相当于是正数截位之前加了个0.5,而负数截位之前对其绝对值减了个0.5.
// round 截位
// 对10bit位宽的 x 截位6bit
assign x1 = x + 10'd32 - {9'd0, x[9]}; // 这里做了3步
assign x2 = x1[9:6]; // 截掉6位
注意:上面的代码还不能直接使用,需要考虑正数+10’d32之后的溢出问题
该方法参考于论文:《数字信号截位影响分析》-- 焦庆君,解剑
.
.
.
.
.
.
.
.
最后
以上就是认真麦片最近收集整理的关于3---不严谨的分析下FPGA设计中的截位—Truncate和Rounding的全部内容,更多相关3---不严谨内容请搜索靠谱客的其他文章。








发表评论 取消回复