写在前面
本文的舍入方法只适用于保留0位或1位小数,个人水平所限,暂时没有发现保留更多小数位的舍入的规律…
IEEE 754的舍入模式
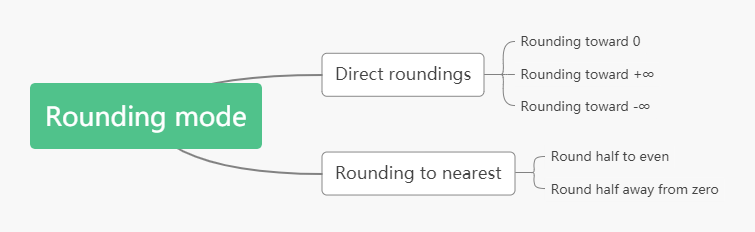
IEEE 754标准提供了2类,5种舍入模式,在默认情况下一般是Round to nearest。
Directed roundings
- Round toward 0
向0舍入,也称截断法
| +11.5 | -11.5 |
|---|---|
| +11.0 | -11.0 |
- Round toward +∞
向正无穷舍入
| +11.5 | -11.5 |
|---|---|
| +12.0 | -11.0 |
- Round toward −∞
向负无穷舍入
| +11.5 | -11.5 |
|---|---|
| +11.0 | -12.0 |
Rounding to nearest
- Round half to even
向最近的偶数舍入
| +23.5 | +24.5 | -23.5 | -24.5 |
|---|---|---|---|
| 24 | 24 | -24 | -24 |
- Round half away from zero
向远离0的方向舍入,也称向无穷方向取整
| +23.5 | +24.5 | -23.5 | -24.5 |
|---|---|---|---|
| 24 | 25 | -24 | -25 |
下面是个人的理解
名称里的"half"在舍入一组数据才比较好的体现出来,如下面的代码所示
#include <stdio.h>
int
main( int argc, char **argv )
{
printf("%.0lfn", 20.5);
printf("%.0lfn", 21.5);
printf("%.0lfn", 22.5);
printf("%.0lfn", 23.5);
printf("%.0lfn", 24.5);
printf("%.0lfn", 25.5);
printf("%.0lfn", 26.5);
printf("%.0lfn", 27.5);
printf("%.0lfn", 28.5);
printf("%.0lfn", 29.5);
return 0;
}
vs2010运行结果
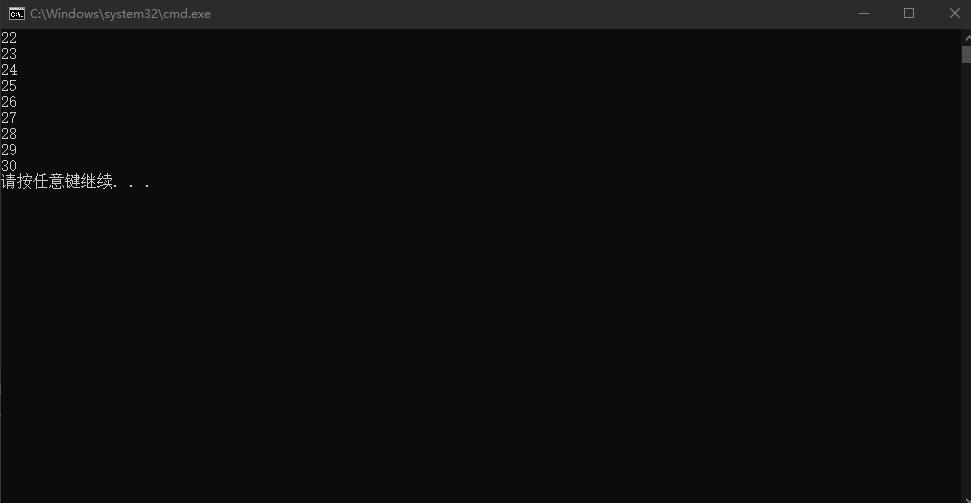
gcc version 7.5.0 (Ubuntu 7.5.0-3ubuntu1~18.04) 运行结果
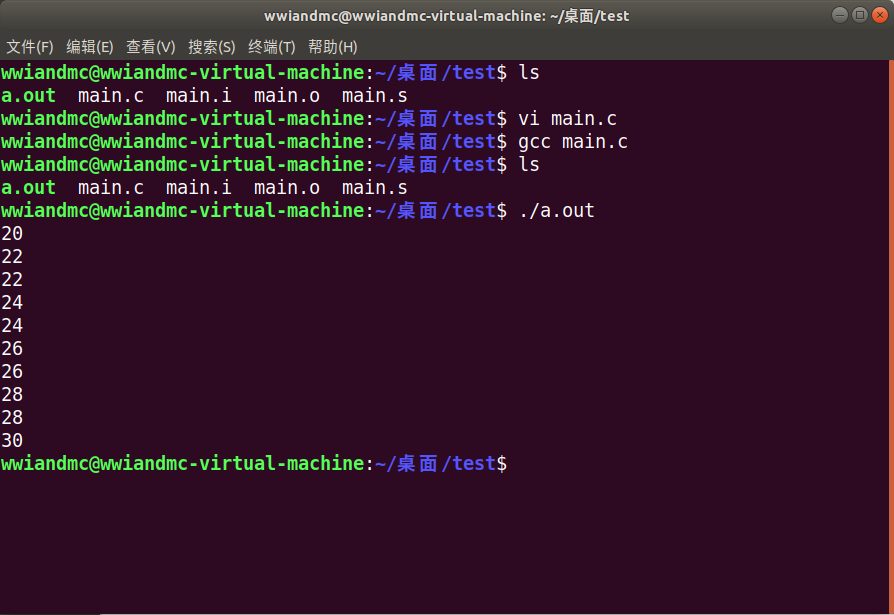
可见vs2010使用的舍入规则是Round half away from zero,gcc使用的是Round half to even。
mingw的gcc运行结果和vs2010一致。
以Ubuntu的运行结果为例,将原数据和舍入后的数据绘制成散点图
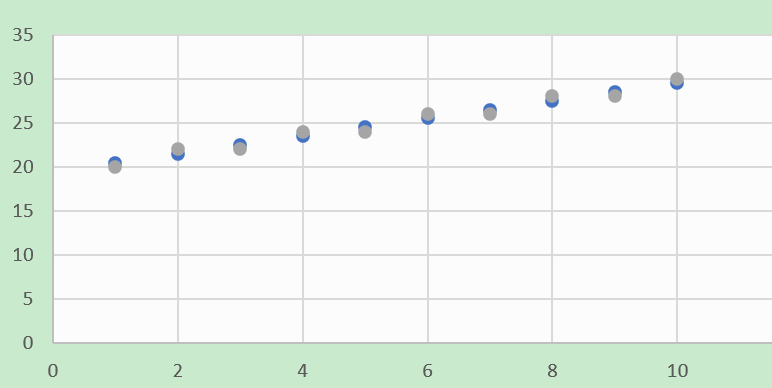
可见,原数据中有的数字是向上取,有的向下取。
更准确的说:是一半的数据向上取整,另一半的数据向下取整。
从图中可以看出,舍入后的数据在原数值上下摆动,但总体上与原数据相差无几。
这便是我理解的half的含义:有一半的数据向下取整,同时另一半的数据向上取整。Round half to even 也是统计学里抵抗误差常用的舍入策略。
下面我们来看看直接四舍五入的散点图
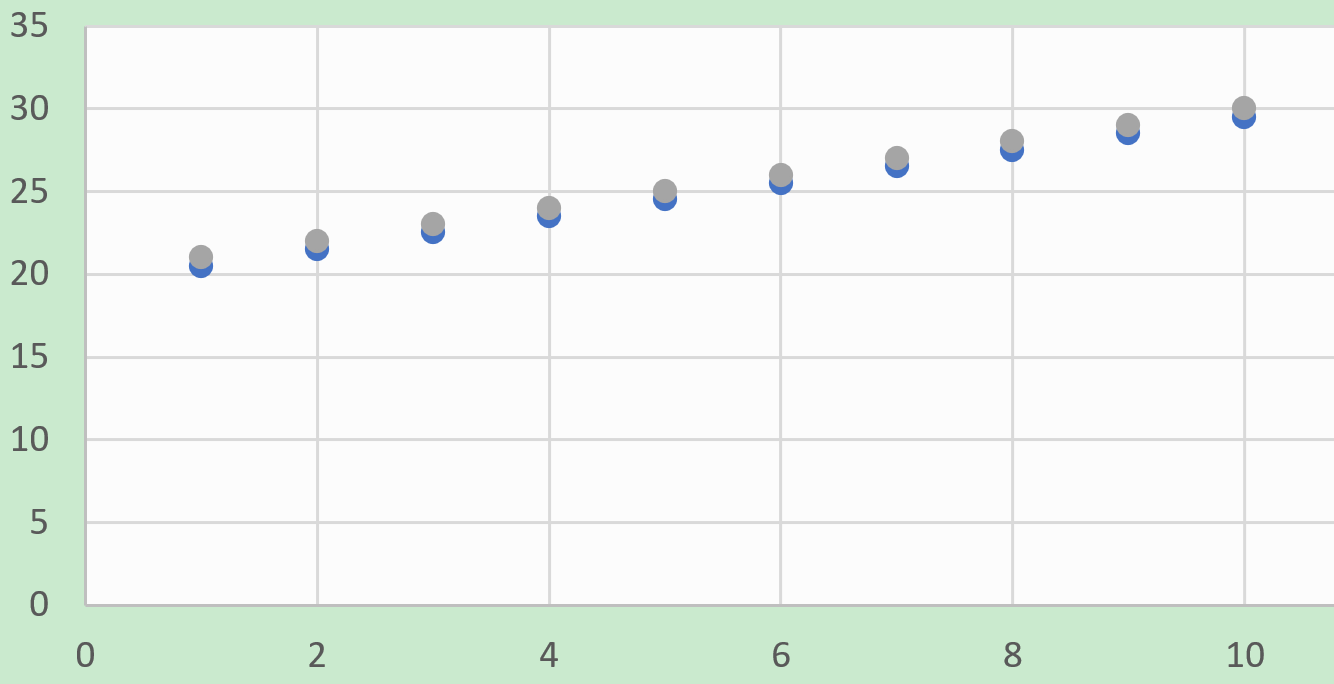
可见,直接四舍五入,所有数据都是向上取整的,舍入误差累积后,舍入后的数据总体上就偏离了原数据。
摘录《深入理解计算机系统》第二章 信息的表示和处理
向偶数舍入初看上去好像是个相当随意的目标——有什么理由偏向取偶数呢?为什么不始终把位于两个可表示的值的中间的值都向上舍入呢?使用这种方法的一个问题就是很容易假想到这样的情景:这种方法舍入一组数据,会在计算这些值的平均数中引入统计偏差。我们采用这种方式舍入得到的一组数的平均值将比这些数本身的平均值略高一些。相反,如果我们总是把两个可表示值中间的数字向下舍入,那么舍入后的一组数的平均值将比这些数本身的平均值略低一些。向偶数舍入在大多数现实情况下避免了这种统计偏差。在50%的时间里,它将向上舍入,而在50%的时间里,它将向下舍入。
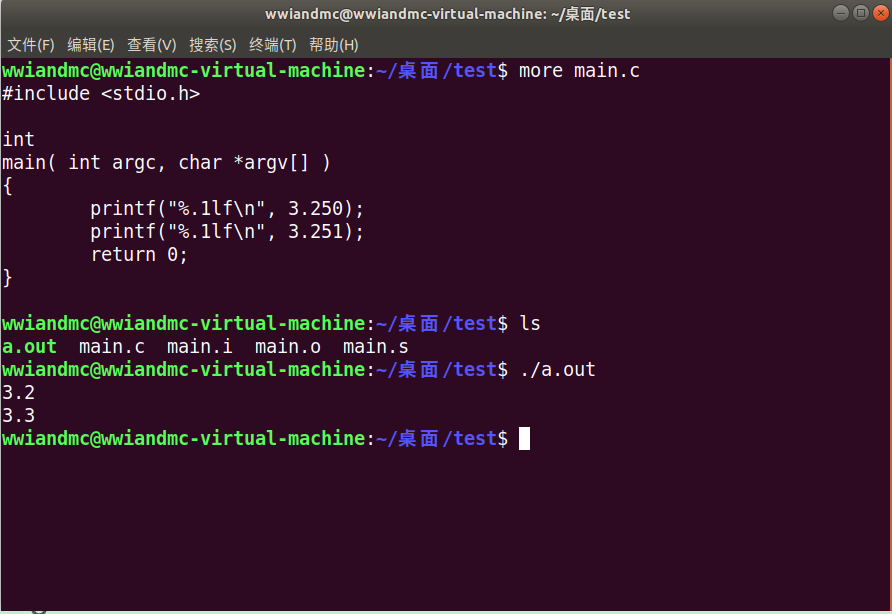
舍入的具体流程 以gcc为例
#include <stdio.h>
int
main( int argc, char **argv )
{
printf("%.1lfn", 3.250);
printf("%.1lfn", 3.251);
return 0;
}
| 数值 | 3.2 | 3.250 | 3.3 |
|---|---|---|---|
| 误差 | 0.05 | 0.05 |
两者误差相同,按照Round half to even,选择最近的偶数3.2
| 数值 | 3.2 | 3.251 | 3.3 |
|---|---|---|---|
| 误差 | 0.051 | 0.049 |
选择误差小的3.3
参考链接
https://my.oschina.net/aquar/blog/731999
https://en.wikipedia.org/wiki/IEEE_754
https://en.wikipedia.org/wiki/Rounding
https://www.zhihu.com/question/68131179/answer/261539674
http://m.newsmth.net/article/EnglishWorld/40696
最后
以上就是冷傲小霸王最近收集整理的关于IEEE 754舍入的问题的全部内容,更多相关IEEE内容请搜索靠谱客的其他文章。








发表评论 取消回复