返回[ ∏C(m_i, n_i) ] × A(k, k), k = ∑(n_i)的所有结果（Matlab实现）

条件

1. 给定有限个非空集合$A_1,A_2,\cdots ,A_m$， ∀ i ∈ { 1 , 2 , ⋯   , m } forall iin left{ 1,2,cdots ,m right} ∀i∈{1,2,⋯,m}，$0<\left|A_i\right|<\infty$，且$\forall i\ne j,A_i\bigcap A_j=\varnothing$。
2. 给定总需求元素个数$N$，$N\in {\mathbb{Z}}_{\ge 1}$且$N\le \sum \left|A_i\right|$。
3. 给定从各个集合$A_i$中抽取元素的个数$n_i$，$n_i\in {\mathbb{Z}}_{\ge 0}$且$n_i\le \left|A_i\right|$，$\sum n_i\le N$，$i=1,2,\cdots ,m$。
   
   

功能
  返回从集合$A_1,A_2,\cdots ,A_m$中挑选出$N$个元素后进行全排列的所有结果。令抽取个数$n_i=0$对应的集合$A_i$的下标构成一个指标集 I 1 = { i : n i = 0 } {{mathcal{I}}_{1}}=left{ i:{{n}_{i}}=0 right} I1​={i:ni​=0}，抽取个数$n_j>0$对应的集合$A_j$的下标构成一个指标集 I 2 = { j : n j > 0 } {{mathcal{I}}_{2}}=left{ j:{{n}_{j}}>0 right} I2​={j:nj​>0}。其中挑选阶段的规则如下：

1. 若$\sum _{i\in {\mathcal{I}}_1}{n}_i=N$，则按照既定要求到指标集${\mathcal{I}}_1$指定的各集合$A_i$里挑选出$n_i$个元素，刚好挑出所需要的$N$个元素。
2. 若$\sum _{i\in {\mathcal{I}}_1}{n}_i<N$，则考虑$\sum _{i\in {\mathcal{I}}_2}\left|A_i\right|$与$N$的关系。若$\sum _{i\in {\mathcal{I}}_2}\left|A_i\right|\ge N-\sum _{i\in {\mathcal{I}}_1}{n}_i$，则在集合$\bigcup _{i\in {\mathcal{I}}_2}{A}_i$中抽取剩下的$N-\sum _{i\in {\mathcal{I}}_1}{n}_i$个元素；否则直接终止计算，要求重新输入合适的数据。
   
   

程序（函数m文件）

function result = c_a( data, N )
%% 函数说明
% 参数
% data -- 是一个 2 * x 的cell, x是所提供集合的个数
%         第一行是每个集合A所拥有的元素的编号（一个编号的元素只能存在于一个集合中）
%         第二行是从对应的集合A里挑选出的元素的个数
% N -- 指定最终要从所有集合里挑选出的总元素的个数
%     （后面需要对这些挑选的元素进行全排列）
% result -- 是一个 y * N 的matrix, 储存从所有集合的所有元素中按照要求
%           挑选出的N个元素的所有排列结果
%           记从n个数选出m个数的组合个数为C(n, m), 从n个数中选出m个数并且进行排列
%           的排列个数为A(n, m), 则有 
%           y = C(n_1, m_1） * C(n_2, m_2) * ... * C(n_x, m_x) * A(N, N)
%
% 功能
%       一次性返回所有的“按照要求从x个集合中总共挑选出N个元素并进行全排列的结果”
%       只适用于集合数较少，每个集合内元素个数较少，挑选总元素个数较少的情况
%       否则需要运行大量时间，或者会出现内存溢出
%
% 例子
% data = { [1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]; ...
%             3, 2, 2 };
% N = 7;
% result = method_1(data, N);

%% 输入参数的检验
[~, column] = size(data);
for i = 1: column
    data{3, i} = numel( data{1, i} );
end

% 对参数N进行检验: 要求挑选的元素总个数N是一个正整数，且不超过所有集合的元素个数和
if floor(N) ~= N || N < 1
    error('元素需求总个数不是一个正整数');
end
if N > sum( cell2mat( data(3, :) ) )
    error('元素需求数大于所有集合的元素个数和');
end

% 对参数data进行检验: 要求
%   1. 提供的每个集合非空;
%   2. 同个集合, 不同集合间均没有重复编号的元素;
%   3. 每个集合挑选元素数是非负整数且不大于集合拥有元素数;
%   4. 所有集合挑选出的元素总数不超过N个.
t = [];
for i = 1: column
    if isempty( data{1, i} )
        error(['第', num2str(i), '个集合是空的']);
    end
    if floor(data{2, i}) ~= data{2, i} || data{2, i} < 0
        error(['第', num2str(i), '个集合的需求数不是一个非负整数']);
    end
    if numel( data{1, i} ) < data{2, i}
        error(['第', num2str(i), '个集合的总元素数小于需求数']); 
    end
    t = [t, data{1, i}];
    if numel(t) ~= numel( unique(t) )
        error(['前', num2str(i), '个集合中至少有两个元素的编号是重复的']);
    end
end
if sum( cell2mat( data(2, :) ) ) > N
    error(['挑选的元素总个数超过了所需求的', num2str(N), '个']);
end

disp('输入参数验证成功');

%% 第一步：确定各个集合的元素挑选方案
result = [];  % 初始化输出参数

% 分别初始化必挑集合（对应data第二行数据非零）和非必挑集合（对应data第二行数据为0）
% 在原data第一行中的索引
nes_set_index = []; unnes_set_index = [];
for i = 1: column
    if data{2, i} == 0
        unnes_set_index = [unnes_set_index, i];
    else
        nes_set_index = [nes_set_index, i];
    end
end

t = { };
% 在各个必挑集合中确定所有的选取方案
for i = nes_set_index
    choices = nchoosek( data{1, i}, data{2, i} );
    [row, ~] = size( choices );
    t = [ t, {choices; row} ];
end

% 计算必挑集合中挑选出的总元素个数
nes_num = 0;
for i = nes_set_index
    nes_num = nes_num + data{2, i};
end

% 若必挑集合挑选的元素还不够要求，则将剩下的非必挑集合并称一个大集合，在这个大集合
% 中确定剩下元素的挑选方案
if nes_num < N
    unnes_set = [];
    for i = unnes_set_index
        unnes_set = [ unnes_set, data{1, i} ];
    end
    
    % 若剩下的非必挑集合的元素总个数足够补足空缺，则需求元素的空缺全部由剩下的
    % 非必挑集合中的元素来补足。
    if ~( N - nes_num > numel(unnes_set) ) 
        choices = nchoosek( unnes_set, N - nes_num );
        [row, ~] = size( choices );
        t = [ t, {choices; row} ];
    
    % 否则直接报错    
    else
        error('无法从刚性挑选约束集合和自由挑选集合中挑选出所需数量的元素');
    end
end

disp('每个集合的元素选择方案已确定');

%% 第二步：每个集合各选一种挑选方案，然后对所有被选元素进行全排列，
%  之后循环遍历得到所有的结果后，再一起输出

[~, column] = size(t);
s = ones(1, column);
times = 1;
while 1
    % 根据s向量每个分量s(i)指定的第i个菜系的挑选结果，拼凑出这7道菜
    recipe = [];
    for i = 1: column
        recipe = [ recipe, t{1, i}( s(i), : )];
    end
    result = [ result; perms(recipe) ];
    
    % 移动mark, 或改变mark指定分量的挑选结果
    mark = column;
    while 1
        if s(mark) < t{2, mark}
            s(mark) = s(mark) + 1;
            disp(['完成了第', num2str(times), '次循环']);
            times = times + 1;
            break
            
        elseif mark > 1
            mark = mark - 1;
            for j = mark + 1 : column
                s(j) = 1;
            end
            
        else
            disp(['完成了第', num2str(times), '次循环']);
            return
        end
    end
end

disp('已生成所有挑选方案的所有排列结果');
end

注
  程序运行过程中输出的“完成了第$x$次循环”，最后输出这个语句时，$x$的值为
$$x=\left(\prod _{i\in {\mathcal{I}}_1}{C}_{|A_i|}^{n_i}\right)C_{\sum _{i\in {\mathcal{I}}_2}|A_i|}^{N-\sum _{i\in {\mathcal{I}}_1}{n}_i}$$

评估
  这种是最粗糙的一种实现方法，函数运行过程中出现和存储的主要的数据就有
$$\left|{\mathcal{I}}_1\right|个组合结果矩阵（规格：C_{|A_i|}^{n_i}\times n_i,i\in {\mathcal{I}}_i）$$
$$1个组合结果矩阵（规格：C_{\sum _{i\in {\mathcal{I}}_2}|A_i|}^{N-\sum _{i\in {\mathcal{I}}_1}{n}_i}\times \left(N-\sum _{i\in {\mathcal{I}}_1}{n}_i\right)）$$
$$1个排列结果矩阵（规格：\left[\left(\prod _{i\in {\mathcal{I}}_1}{C}_{|A_i|}^{n_i}\right)C_{\sum _{i\in {\mathcal{I}}_2}|A_i|}^{N-\sum _{i\in {\mathcal{I}}_1}{n}_i}{A}_N^N\right]\times N）$$可见内存使用量是很大的（因为储存了所有的排列结果）。因此该程序只适用于集合数较少，集合含元素个数较少，需求元素个数较少的情况。

例子

data = { [1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]; 3, 2, 2 };
N = 7;
tic
result = c_a( data, N );
toc

结果

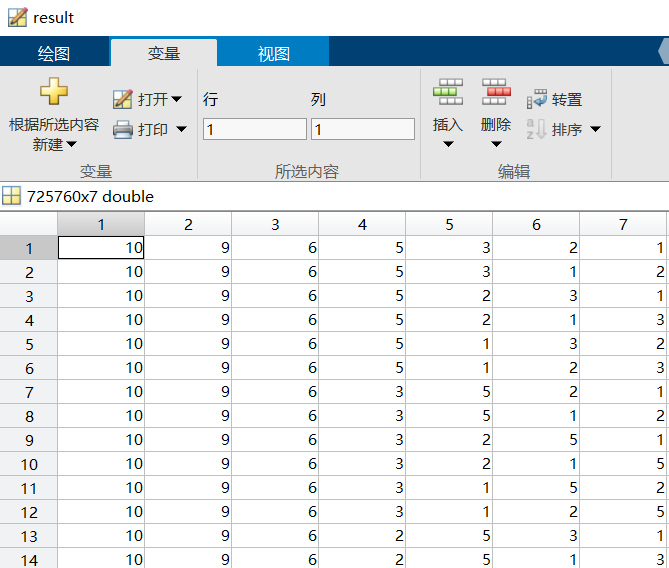
最后

以上就是无奈小天鹅为你收集整理的返回[ ∏C(m_i, n_i) ] × A(k, k), k = ∑(n_i)的所有结果（Matlab实现）的全部内容，希望文章能够帮你解决返回[ ∏C(m_i, n_i) ] × A(k, k), k = ∑(n_i)的所有结果（Matlab实现）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。