文章目录
- 定义
- 对比模拟捕食
- 通俗解释
- 粒子抽象
- 关于速度和位置
- 速度和位置的更新
- 标准PSO算法流程
- 标准PSO算法的流程
- PSO流程图解
- 学习因子 c 1 、 c 2 c_1、c_2 c1、c2 分析
- 仿真(Matlab)
- 仿真1
- 仿真2
- Ref.
定义
粒子群优化算法(Particle Swarm optimization,PSO)又翻译为粒子群算法、微粒群算法、或微粒群优化算法。是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。通常认为它是群集智能 (Swarm intelligence, SI) 的一种。它可以被纳入多主体优化系统(Multiagent Optimization System, MAOS)。粒子群优化算法是由Eberhart博士和kennedy博士发明。
对比模拟捕食
PSO模拟鸟群的捕食行为。一群鸟在随机搜索食物,在这个区域里只有一块食物。所有的鸟都不知道食物在那里。但是他们知道当前的位置离食物还有多远。那么找到食物的最优策略是什么呢。最简单有效的就是搜寻离食物最近的鸟的周围区域。
PSO从这种模型中得到启示并用于解决优化问题。PSO中,每个优化问题的解都是搜索空间中的一只鸟。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitnessvalue),每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。
PSO初始化为一群随机粒子(随机解),然后通过迭代找到最优解,在每一次迭代中,粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解,这个解叫做个体极值 p b e s t p^{best} pbest,另一个极值是整个种群找到的最优解,这个极值是全局极值 g b e s t g^{best} gbest。另外也可以不用整个种群而只是用其中一部分最优粒子的邻居,那么在所有邻居中的极值就是局部极值。
通俗解释
粒子群算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。如上的情景。试着想一下一群鸟在寻找食物,在这个区域中只有一只虫子,所有的鸟都不知道食物在哪。但是它们知道自己的当前位置距离食物有多远,同时它们知道离食物最近的鸟的位置。想一下这时候会发生什么?

同时各只鸟在位置不停变化时候离食物的距离也不断变化,所以每个鸟一定有过离食物最近的位置,这也是它们的一个参考。

粒子抽象
关于速度和位置
粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟,粒子仅具有两个属性:速度 v v v 和位置 p p p,速度代表移动的快慢,位置代表移动的方向。
鸟被抽象为没有质量和体积的微粒(点),并延伸到 N N N 维空间,粒子 i i i 在 N N N 维空间的位置表示为矢量 X i = ( x 1 , x 2 , ⋯ , x N ) X_i=(x_1,x_2,cdots,x_N) Xi=(x1,x2,⋯,xN),飞行速度表示为矢量 V i = ( v 1 , v 2 , ⋯ , v N ) V_i=(v_1,v_2,cdots,v_N) Vi=(v1,v2,⋯,vN)。每个粒子都有一个由目标函数决定的适应值(fitness value),并且知道自己到目前为止发现的最好位置( p b e s t p^{best} pbest )和现在的位置 X i X_i Xi。这个可以看作是粒子自己的飞行经验。除此之外,每个粒子还知道到目前为止整个群体中所有粒子发现的最好位置( g b e s t g^{best} gbest)( g b e s t g^{best} gbest 是 p b e s t p^{best} pbest 中的最好值),这个可以看作是粒子同伴的经验。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。
已知条件包括:
- p b e s t p^{best} pbest
- X i X_i Xi
- g b e t s g^{bets} gbets
速度和位置的更新
PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次的迭代中,粒子通过跟踪两个“极值”(pbest,gbest)来更新自己。在找到这两个最优值后,粒子通过下面的公式来更新自己的速度和位置。
速度更新公式:
V
i
=
V
i
⏟
记
忆
项
+
c
1
∗
rand
(
)
∗
(
p
b
e
s
t
−
X
i
)
⏟
自
身
认
知
项
+
c
2
∗
rand
(
)
∗
(
g
b
e
s
t
−
X
i
)
⏟
群
体
认
知
项
(1)
V_i = underbrace{red{V_i}}_{记忆项} + underbrace{green{c_1 * text{rand}() * (p^{best} - X_i)}}_{自身认知项} + underbrace{blue{c_2 * text{rand}() * (g^{best} - X_i)}}_{群体认知项} tag{1}
Vi=记忆项
Vi+自身认知项
c1∗rand()∗(pbest−Xi)+群体认知项
c2∗rand()∗(gbest−Xi)(1)
V
i
V_i
Vi: 粒子
i
i
i 的速度;
rand
(
)
text{rand}()
rand(): 介于 (0,1) 之间的随机数;
X
i
X_i
Xi: 粒子
i
i
i 的位置;
c
1
,
c
2
c_1, c_2
c1,c2: 学习因子,通常
c
1
=
c
2
=
2
c_1 = c_2 = 2
c1=c2=2;
V
m
a
x
V_{max}
Vmax: 为
V
i
V_i
Vi 的最大值(>0),如果
V
i
>
V
m
a
x
V_i > V_{max}
Vi>Vmax,则
V
i
=
V
m
a
x
V_i = V_{max}
Vi=Vmax。
- 记忆项。表示上次速度大小和方向的影响;
- 自身认知项。是从当前点指向粒子自身最好点的一个矢量,表示粒子的动作来源于自己经验的部分;
- 群体认知项。是一个从当前点指向种群最好点的矢量,反映了粒子间的协同合作和知识共享。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。
位置更新公式:
X
i
=
X
i
+
V
i
(2)
X_i = X_i + V_i tag{2}
Xi=Xi+Vi(2)
上述公式(1)(2)为 PSO 的标准形式。
以上面两个公式为基础,再来看一个公式:
V
i
=
ω
∗
V
i
+
c
1
∗
rand
(
)
∗
(
p
b
e
s
t
−
X
i
)
+
c
2
∗
rand
(
)
∗
(
g
b
e
s
t
−
X
i
)
(3)
V_i = omega * red{V_i} + green{c_1 * text{rand}() * (p^{best} - X_i)} + blue{c_2 * text{rand}() * (g^{best} - X_i)} tag{3}
Vi=ω∗Vi+c1∗rand()∗(pbest−Xi)+c2∗rand()∗(gbest−Xi)(3)
ω
omega
ω: 惯性因子,值为非负 (
≥
0
ge0
≥0)。
其值较大,则全局寻优能力强,局部寻优能力弱;
其值较小,则全局寻优能力弱,局部寻优能力强。
动态
ω
omega
ω 能获得比固定值更好的寻优效果。动态
ω
omega
ω 可在 PSO 搜索过程中线性变化,也可以根据 PSO 性能的某个测度函数动态改变。
目前采用较多的线性递减权值(Linearly Decreasing Weight, LDW)策略。
ω
(
t
)
=
(
ω
i
n
i
−
ω
g
n
d
)
(
G
k
−
g
)
/
G
k
+
ω
g
n
d
omega^{(t)} = (omega_{ini} - omega_{gnd}) (G_k - g) / G_k + omega_{gnd}
ω(t)=(ωini−ωgnd)(Gk−g)/Gk+ωgnd
G
k
G_k
Gk: 最大迭代次数;
ω
i
n
i
omega_{ini}
ωini: 初始惯性权值;
ω
g
n
d
omega_{gnd}
ωgnd: 迭代至最大进化代数时的惯性权值
典型权值:
ω
i
n
i
=
0.9
,
ω
g
n
d
=
0.4
omega_{ini} = 0.9, omega_{gnd} = 0.4
ωini=0.9,ωgnd=0.4。
ω
omega
ω 的引入,使 PSO 算法性能有了很大的提高,针对不同的搜索问题,可以调整全局和局部搜索能力,也使 PSO 算法有成功地应用于很多实际问题。
公式(2)和 公式(3)被视为标准PSO算法。
标准PSO算法流程
标准PSO算法的流程
1)初始化一群微粒(群体规模为 N N N ),包括随机位置和速度;
2)评价每个微粒的适应度;
3)对每个微粒,将其适应值与其经过的最好位置 p b e s t p^{best} pbest作比较,如果较好,则将其作为当前的最好位置 p b e s t p^{best} pbest;
4)对每个微粒,将其适应值与其经过的最好位置 g b e s t g^{best} gbest 作比较,如果较好,则将其作为当前的最好位置 g b e s t g^{best} gbest;
5)根据公式(2)、(3)调整微粒速度和位置;
6)未达到结束条件则转第2)步。
迭代终止条件根据具体问题一般选为最大迭代次数 G k G_k Gk 或(和)微粒群迄今为止搜索到的最优位置满足预定最小适应阈值。
PSO流程图解
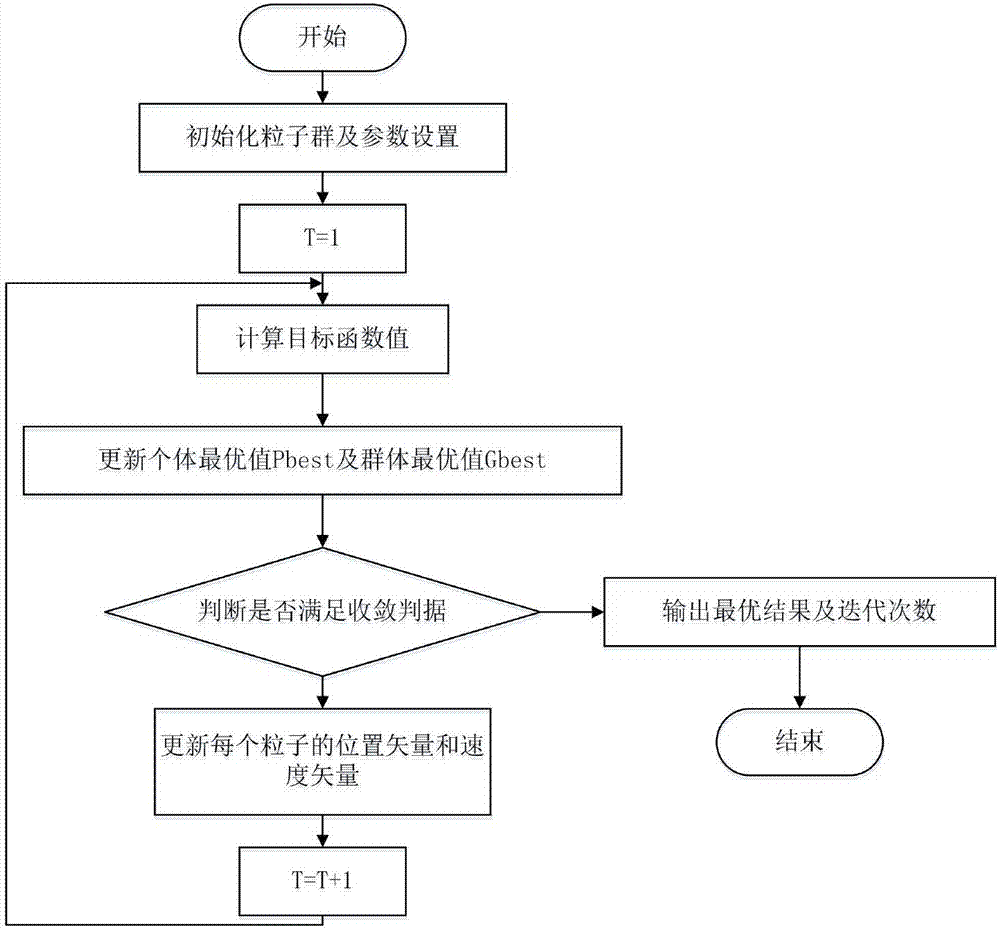
学习因子 c 1 、 c 2 c_1、c_2 c1、c2 分析
公式(2)和(3)中 p b e s t p^{best} pbest 和 g b e s t g^{best} gbest 分别表示微粒群的局部和全局最优位置。
当
c
1
=
0
c_1=0
c1=0 时,则粒子没有了认知能力,变为只有社会的模型(social-only):
称为全局PSO算法。粒子有扩展搜索空间的能力,具有较快的收敛速度,但由于缺少局部搜索,对于复杂问题比标准PSO 更易陷入局部最优。
当
c
2
=
0
c_2=0
c2=0 时,则粒子之间没有社会信息,模型变为只有认知(cognition-only)模型:
称为局部PSO算法。由于个体之间没有信息的交流,整个群体相当于多个粒子进行盲目的随机搜索,收敛速度慢,因而得到最优解的可能性小。
仿真(Matlab)
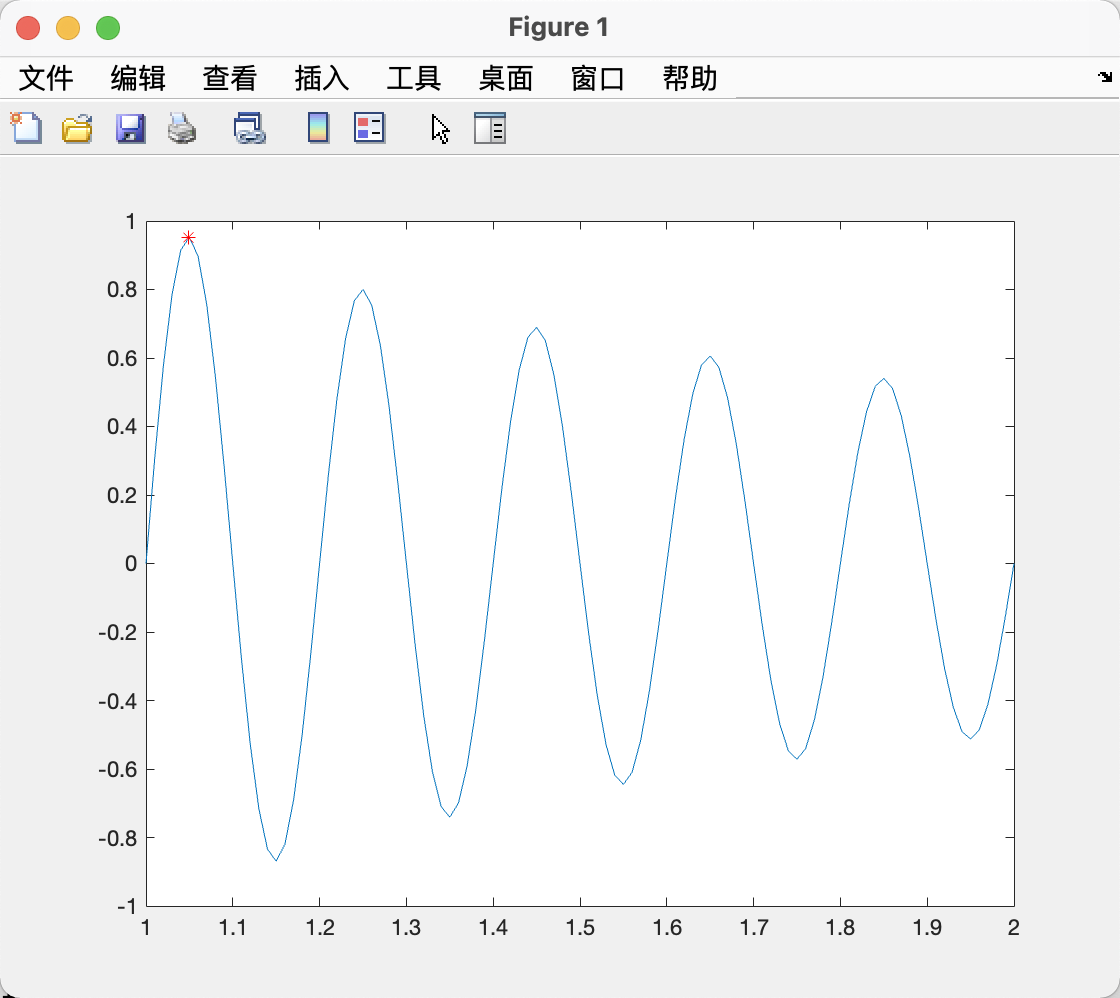
仿真1
% PSO
% Author: Zhao-Jichao
% Date: 2021-10-06
clc
clear
%% Target Function
x = 1:0.01:2;
y = sin(10 * pi * x) ./ x;
figure(1)
plot(x, y)
hold on
title("目标函数曲线");
%% Parameters Initialized
X = zeros(10,1);
V = zeros(10,1);
fun=@(x) sin(10 * pi * x) ./ x; % 定义被优化函数
fitness = zeros(10,1); % 由被优化的函数决定的适应值
c1 = 1.49445; % 学习因子
c2 = 1.49445;
Gk = 50; % 进化次数
N = 10; % 种群规模
Vmax = 0.5; % 速度的范围,超过则用边界值。
Vmin = -0.5;
Nmax = 2; % 个体的变化范围
Nmin = 1;
%% 产生初始粒子和速度
for i = 1:N
% 随机产生一个种群
X(i,:) = (rands(1) + 1) / 2 + 1; % 初始种群位置,rands产生(-1,1),调整到(1,2)
V(i,:) = 0.5 * rands(1); % 初始化速度
fitness(i) = fun(X(i,:)); % 计算适应度
end
%% 个体极值和群体极值
[bestfitness, bestindex] = max(fitness);
gbest = X(bestindex,:); % 全局最佳
pbest = X; % 个体最佳
fitnessgbest = bestfitness; % 全局最佳适应度值
fitnesspbest = fitness; % 个体最佳适应度值
%% VI. 迭代寻优
for i = 1:Gk
for j = 1:N
% 速度更新
V(j,:) = V(j,:) + c1*rand*(pbest(j,:)-X(j,:)) + c2*rand*(gbest-X(j,:));
V(j,V(j,:)>Vmax) = Vmax;
V(j,V(j,:)<Vmin) = Vmin;
% 种群更新
X(j,:) = X(j,:) + V(j,:);
X(j,X(j,:)>Nmax) = Nmax;
X(j,X(j,:)<Nmin) = Nmin;
% 适应度值更新
fitness(j) = fun(X(j,:));
end
for j = 1:N
% 个体最优更新
if fitness(j) > fitnesspbest(j)
pbest(j,:) = X(j,:);
fitnesspbest(j) = fitness(j);
end
% 群体最优更新
if fitness(j) > fitnessgbest
gbest = X(j,:);
fitnessgbest = fitness(j);
end
end
yy(i) = fitnessgbest;
end
%% 输出结果并绘图
[gbest, fitnessgbest]
plot(gbest, fitnessgbest,'r*')
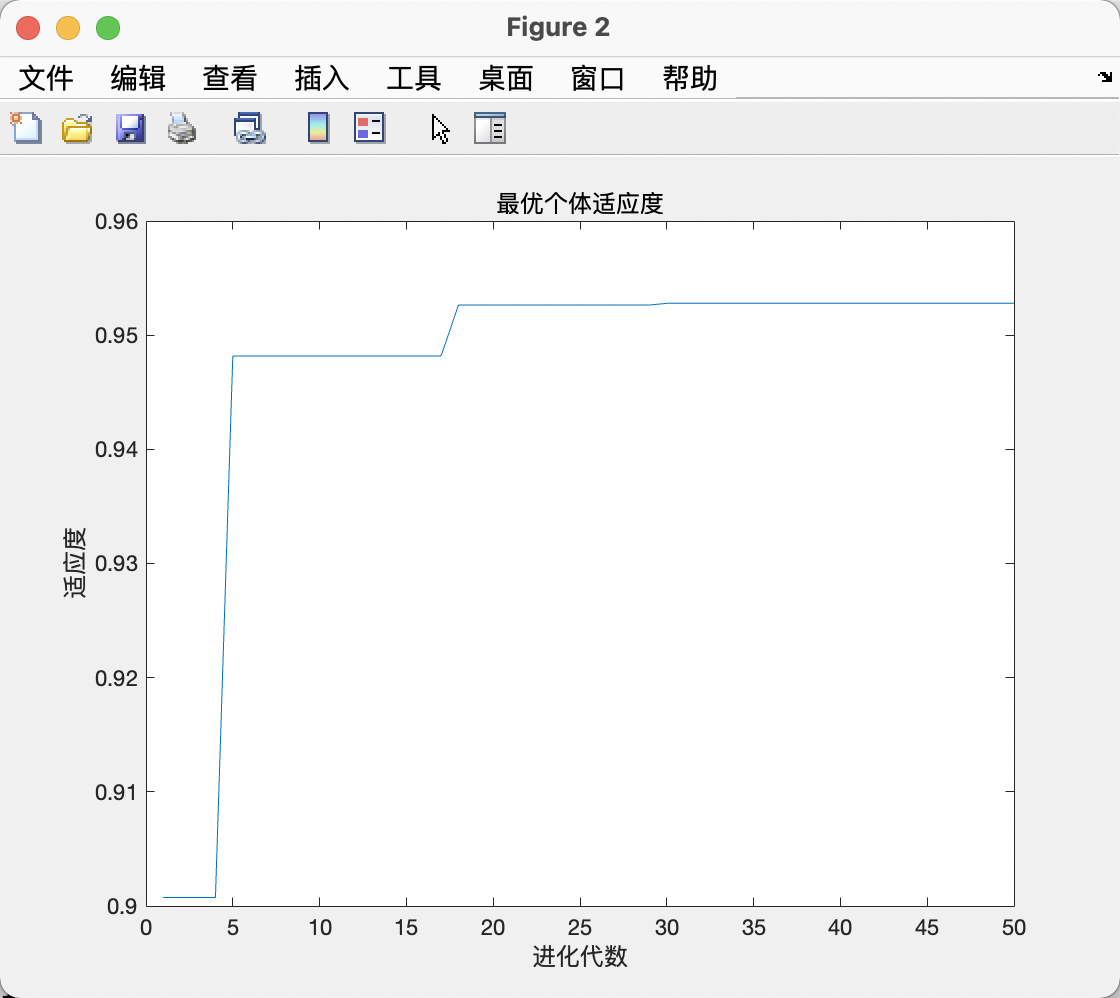
figure(2)
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);
仿真2
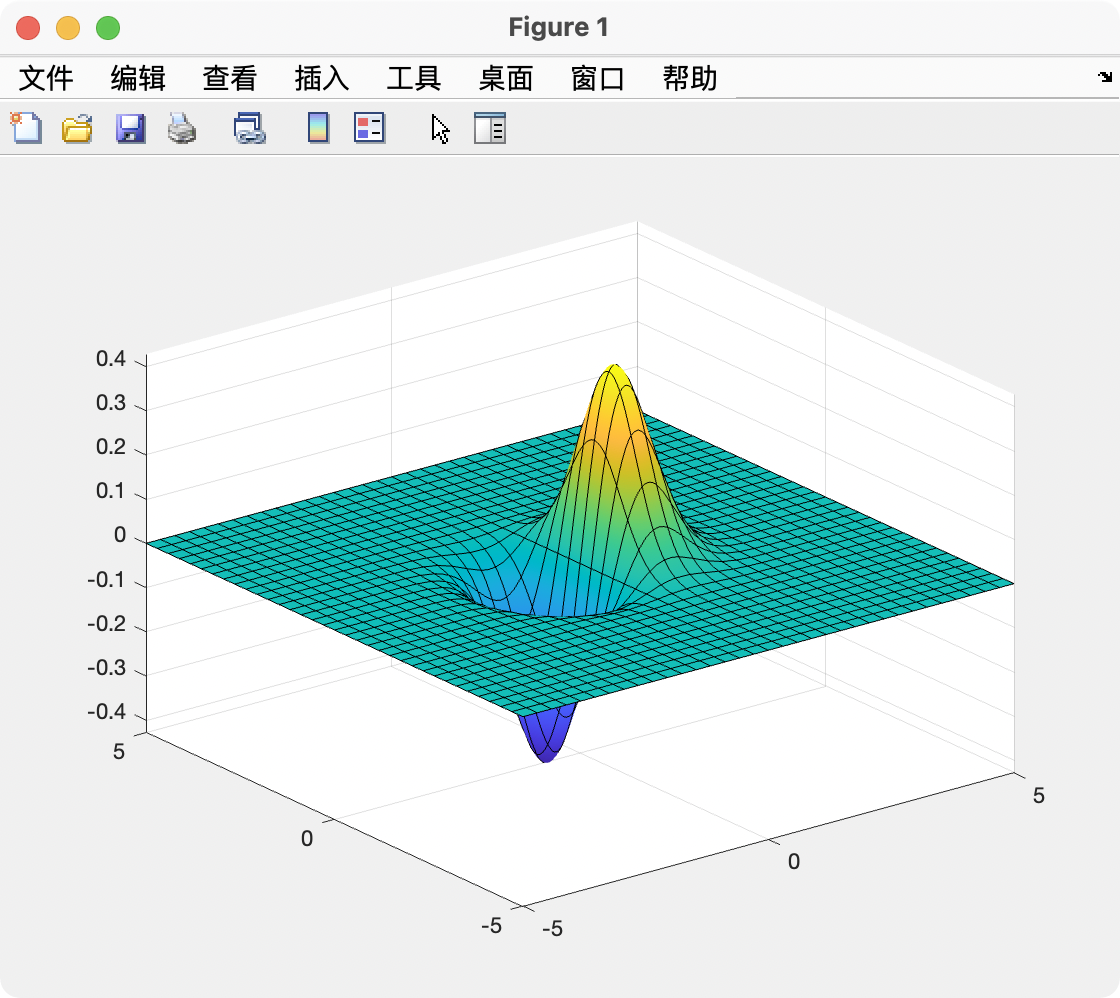
fun = @(x)x(1)*exp(-norm(x)^2);
rng default % For reproducibility
nvars = 2;
x = particleswarm(fun,nvars)
fsurf(@(x,y)x.*exp(-(x.^2+y.^2)))
Ref.
- 粒子群优化算法-百度百科
- 【算法】粒子群算法Particle Swarm Optimization超详细解析+代码实例讲解
- 粒子群优化算法(PSO)简介及MATLAB实现
- particleswarm-MathWorks
最后
以上就是包容店员最近收集整理的关于【控制】粒子群优化(PSO,Particle Swarm Optimization)算法及 Matlab 仿真实现定义对比模拟捕食通俗解释粒子抽象标准PSO算法流程仿真(Matlab)Ref.的全部内容,更多相关【控制】粒子群优化(PSO,Particle内容请搜索靠谱客的其他文章。








发表评论 取消回复