概述
Matlab-NURBS工具箱使用教程
添加NURBS工具箱
在附加功能里添加NURBS工具箱
安装完成后可以在’函数’处查看API，也打开文件夹查看。
强烈推荐同步安装gnurbs工具，它完全代替nrbplot展示曲面，且允许用户进行节点拖拽等操作。
NURBS 结构：
曲线和曲面都由一个结构表示
与 Mathworks 的样条工具箱兼容
nurbs.form … 输入名称’B-NURBS’
nurbs.dim … 控制点的尺寸
nurbs.number … 控制点数
nurbs.coefs … 控制点
nurbs.order … 样条的阶数
nurbs.knots … 节点向量
关键API的用法
我们打开文件夹发现工具箱由4个脚本及55个函数组成：
- Contents.m —工具箱目录，包含36个API；
% demos- NURBS 演示
% nrbmak - 从控制点和节点构建 NURBS。
% nrbtform - 缩放、平移或旋转的变换矩阵。
% nrbkntins - 节点插入/细化。
% nrbdegelev - 度数提升。
% nrbderiv - NURBS 的导数结构。
% nrbdeval - NURBS 导数的求解。
% nrbkntmult - 求节点的多重性。
% nrbreverse - NURBS节点及核改为逆序并重构 。
% nrbtransp - 交换 NURBS 曲面的 U 和 V。
% nrbline - 构建NURBS表示的一条直线。
% nrbcirc - 构建NURBS表示的一个圆弧。
% nrbrect - 构造NURBS表示的一个矩形。
% nrb4surf - 由 4 个角点定义的一个面片。
% nrbeval - NURBS 曲线或曲面的求值。
% nrbextrude - 沿向量挤出 NURBS 曲线。
% nrbrevolve - 通过旋转轮廓构建曲面。
% nrbruled - 在两条NURBS 曲线之间生成直纹曲面。
% nrbcoons - 由4条NURBS曲线构造 Coons 双线性混合表面。
% nrbplot - 绘制 NURBS 曲线或曲面。
% bspeval - 单变量 B 样条求值。
% bspderiv - 导数的 B 样条表示。
% bspkntins - 在单变量 B 样条中插入一个或多个节点。
% bspdegelev - 单变量 B 样条的度数提升。
%下面的是里面带的，很简单，可用可不用
% vecnorm - 向量规范化拼接。
% vecmag - 向量的内积开方。
% vecmag2 - 向量的内积。
% vecangle - 求对应向量分量的tan值（0 <= 角度 <= 2*pi）
% vecdot - 两个向量的点积。
% veccross - 两个向量的叉积。
% vecrotx - 围绕 x 轴的旋转矩阵。
% vecroty - 围绕 y 轴的旋转矩阵。
% vecrotz - 围绕 z 轴的旋转矩阵。
% vecscale - 缩放矩阵。
% vectrans - 平移矩阵。
%
% deg2rad - 将度数转换为弧度。
% rad2deg - 将弧度转换为度数。
- nrbmak - 从控制点和节点构建 NURBS。
nurbs = nrbmak(coefs,knots)
nrbmak - 给定控制点，构造 NURBS 结构和结。
参数：
cntrl : 控制点，这些可以是笛卡尔或齐次坐标。
对于曲线，控制点由大小为 (dim,nu) 的矩阵
表示，对于曲面，控制点由大小为 (dim,nu,nv)
的多维数组表示。 其中 nu 是沿参数 U 方向
的点数，nv 是沿 V 方向的点数。
Dim 是维度有效选项
2 .... (x,y) 二维笛卡尔坐标
3 .... (x,y,z) 3D 笛卡尔坐标
4 .... (wx,wy,wz,w) 4D齐次坐标
knots : 非递减结序列，跨越区间[0.0,1.0]假设曲线和曲
面通过等于样条阶数的节点多重性被夹紧到
起点和终点控制点。 对于曲线A形成一个向
量，对于曲面A由U和V的两个向量存储在一
个单元结构中。
{uknots vknots}
nurbs ： 用于表示 NURBS 曲线的数据结构。
注意：控制点始终在 NURBS 结构中转换并存储为
4D 齐次坐标。 一条曲线总是沿 U 方向存储，
vknots 元素是一个空矩阵。 对于曲面，样条
度数是一个向量 [du,dv]，分别包含沿 U 和 V 方向的度数。
描述：
这个函数是用来构建NURBS数据结构的一个常用函数。
工具箱中的许多其他函数都依赖于 NURBS结构的正确定义。
nrbmak 不仅构建了正确的结构，而且还检查了一致性。
用户仍然可以自由地建立自己的结构，
事实上工具箱中的函数就是为了方便而做的。
案例1
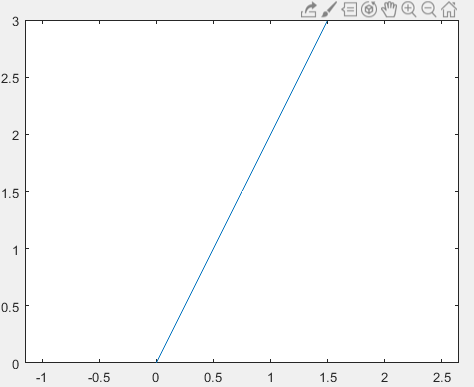
构造一条从 (0.0,0.0) 到 (1.5,3.0) 的二维线。对于直线，需要 2 阶样条。
请注意，结序列在开始 (0.0,0.0) 和结束 (1.0 1.0) 处的重数为 2，以便夹紧末端。
line = nrbmak([0.0 1.5; 0.0 3.0],[0.0 0.0 1.0 1.0]);
nrbplot(line, 2);
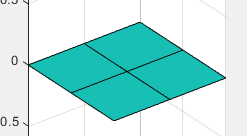
案例2
在 x-y 平面上构造一个曲面，
line = nrbmak([0.0 1.5; 0.0 3.0],[0.0 0.0 1.0 1.0]);
nrbplot(line, 2);
coefs = cat(3,[0 0; 0 1],[1 1; 0 1]);
knots = {[0 0 1 1] [0 0 1 1]}
plane = nrbmak(coefs,knots);
nrbplot(plane, [2 2]);
3.nrbdegelev - 度数提升。
对于度数我一直没理解上去，仿佛只是控制点分化了，每个节点升一度多分化一个
可详间曲线度数提升章节
inurbs = nrbdegelev(nurbs, ntimes)
% nrbdegelev - 提高 NURBS 曲线或曲面的度数。
%
% 调用序列：
%
% ecrv = nrbdegelev(crv,utimes);
% esrf = nrbdegelev(srf,{utimes,vtimes});
%
％ 参数：
%
% crv ：NURBS 曲线，参见 nrbmak。
% srf ：NURBS 曲面，参见 nrbmak。
% utimes : 增加沿 U 方向的度数。
% vtimes : 增加沿 V 方向 vtimes 的度数。
% ecrv ：曲线的新 NURBS 结构，度数升高。
% esrf ：度数升高的表面的新 NURBS 结构。
%
％ 描述：
% degree 提升 NURBS 曲线或曲面。
此函数使用 B-Spline 函数 bspdegelev，它与内部“C”例程接口。
%
％ 例子：
%
% 沿 V 方向增加 NURBS 曲面两次。
% esrf = nrbdegelev(srf, 0, 1);
- nrbreverse - NURBS节点及核改为逆序并重构 。
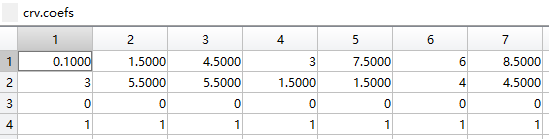
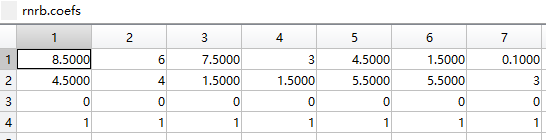
crv = nrbtestcrv; %加载测试用的nurbs曲线
rcrv=nrbreverse(crv); %反转
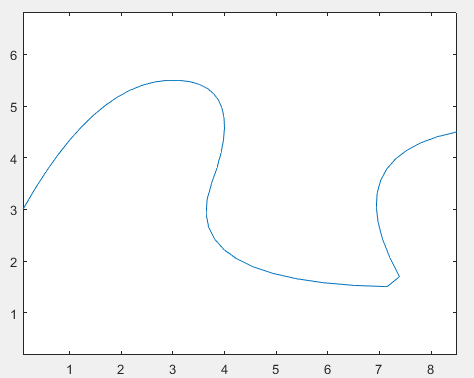
- 案例----构建直纹曲面
%如果一个曲面可以由一条直线通过连续运动构成，则可称其为直纹曲面。
%最常见的直纹曲面是平面、柱面和锥面。著名的莫比乌斯环也是直纹曲面。
%假如一个曲面上的任意一点均有两条不同的直线经过，
%那么称该曲面为双重直纹曲面。双曲抛物面和单叶双曲面即为双重直纹曲面的典型例子。
%对于曲面上每个点均有三条或更多的直线经过的曲面，可称为三重和多重直纹曲面。
%不过在三维欧几里得空间中，除了平面以外，不存在这样的直纹曲面。
hold on
title('由两条NURBS曲线构成的规则曲面.');
crv1 = nrbtestcrv; %构建一个简单的测试曲线。
% nrbcirc - 构建一个nubrs圆弧。 vectrans-生成变换矩阵
% 半径,中心,起始角度,结束角度 xyz的变化
crv2 = nrbtform(nrbcirc(4,[4.5;4],pi,0.0),vectrans([0.0 0 -4.0]));
srf = nrbruled(crv1,crv2); %在两条线间构建直纹曲面
nrbplot(srf,[40 20]); %绘制nurbs曲线/曲面
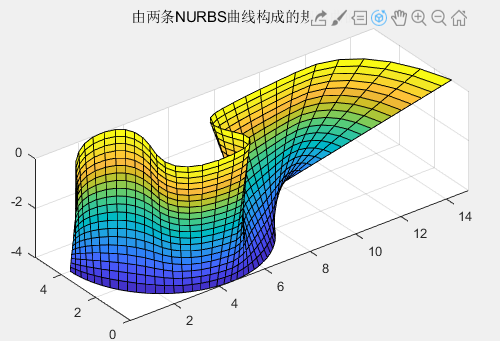
- 案例----度数提升算法演示.
crv = nrbtestcrv; %加载测试曲线
% 绘制控制点
plot(crv.coefs(1,:),crv.coefs(2,:),'bo') %画点
title('测试曲线度数提升1');
hold on;
plot(crv.coefs(1,:),crv.coefs(2,:),'b--'); %连线
% 绘制Nurbs曲线
nrbplot(crv,48);
% 度提升的曲线 by 1
icrv = nrbdegelev(crv, 1);
nrbplot(icrv,50)
% 插入新的结点并绘制新的控制点
plot(icrv.coefs(1,:),icrv.coefs(2,:),'ro') %画点
plot(icrv.coefs(1,:),icrv.coefs(2,:),'r--'); %连线
hold off;
提升1度
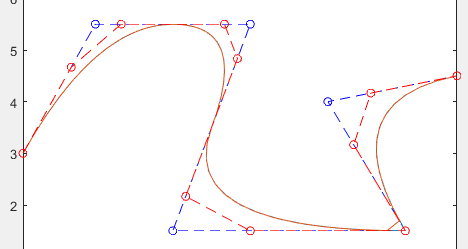
提升2度
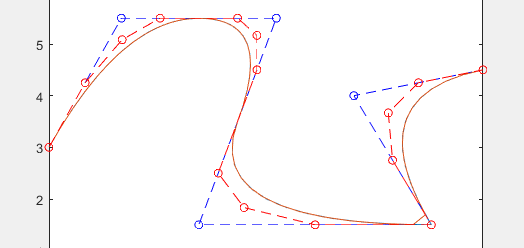
提升3度
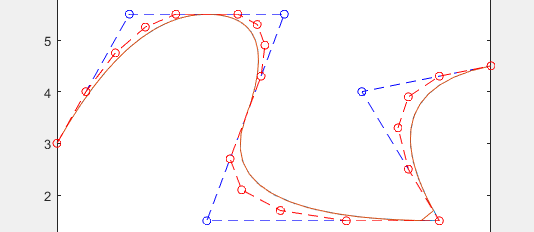
在升一度下再升2度、在升2度下再升一度、提升3度
其三者结果相同，结构体也一样，望留言解答。
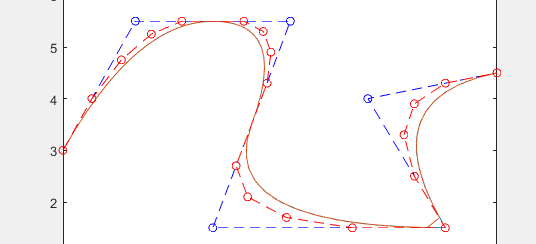
nrbtestcrv函数
function crv = nrbtestcrv
pnts = [0.1 1.5 4.5 3.0 7.5 6.0 8.5;
3.0 5.5 5.5 1.5 1.5 4.0 4.5;
0.0 0.0 0.0 0.0 0.0 0.0 0.0];
crv = nrbmak(pnts,[0 0 0 1/4 1/2 3/4 3/4 1 1 1]);
- 案例----构建双线性混合的昆氏曲面
%昆氏曲面英文coons曲面，是基于四边形面片的一种曲面构造方法。
%首先要理解引导方向缀面数和截断方向缀面数的意思（相互垂直的方向）。
%从引导方向上顺延过去，有几个面，那么缀面数就是多少；截断方向缀面数也一样。
%譬如一个四面片，那么从任何一个方向的缀面数都是1。
%如果两个四面片相接，那么一个方向的缀面数是2，另外一个是1。
%如果是一个“田”字型的4个四边形面片组成的，那么引导和截断方向缀面数都是2。
%在连接的时候先连引导方向的线，每次都是一个四边形面片的一边，
%注意看提示。如果特殊的，譬如三角面片，那就把点重复。
% 边界 曲线 1
pnts = [ 0.0 3.0 4.5 6.5 8.0 10.0;
0.0 0.0 0.0 0.0 0.0 0.0;
2.0 2.0 7.0 4.0 7.0 9.0];
crv1 = nrbmak(pnts, [0 0 0 1/3 0.5 2/3 1 1 1]);
% 边界 曲线 2
pnts= [ 0.0 3.0 5.0 8.0 10.0;
10.0 10.0 10.0 10.0 10.0;
3.0 5.0 8.0 6.0 10.0];
crv2 = nrbmak(pnts, [0 0 0 1/3 2/3 1 1 1]);
% 边界 曲线 3
pnts= [ 0.0 0.0 0.0 0.0;
0.0 3.0 8.0 10.0;
2.0 0.0 5.0 3.0];
crv3 = nrbmak(pnts, [0 0 0 0.5 1 1 1]);
% 边界 曲线 4
pnts= [ 10.0 10.0 10.0 10.0 10.0 ;
0.0 3.0 5.0 8.0 10.0 ;
9.0 7.0 7.0 10.0 10.0 ];
crv4 = nrbmak(pnts, [0 0 0 0.25 0.75 1 1 1]);
srf = nrbcoons(crv1, crv2, crv3, crv4); %双线性混合昆氏曲面的构建
% 绘制表面
nrbplot(srf,[20 20]);
title('双线性混合昆氏曲面的构建。');
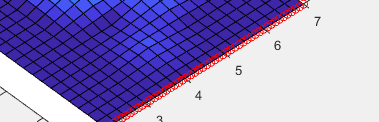
8. 案例----多控制点的曲面生成
例子1
pnts(:,:,1) =[2 3 4 5 6 7;
0 0 0 0 0 0;
4 4 4 4 4 4];
pnts(:,:,2) =[2 3 4 5 6 7;
1 1 1 1 1 1;
4 4 4.1 4 4 4];
pnts(:,:,3) =[2 3 4 5 6 7;
2 2 2 2 2 2;
4 4 4 4.2 4 4];
pnts(:,:,4)= [2 3 4 5 6 7;
3 3 3 3 3 3;
4 4 4.3 4 4 4];
pnts(:,:,5)= [2 3 4 5 6 7;
4 4 4 4 4 4;
4 4 4.4 4 4 4];
knots{1} = [0 0 1/5 2/5 3/5 4/5 1 1]; %u
knots{2} = [0 0 1/4 2/4 3/4 1 1]; %v
plane = nrbmak(pnts,knots);
nrbplot(plane, [50 50]);
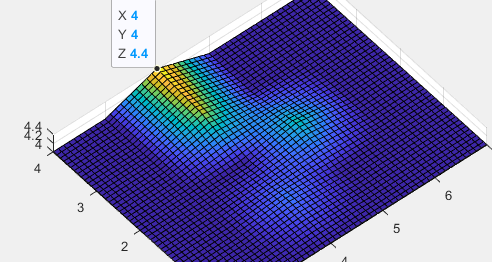
难点在于knots{1}与knots{2}
knots{1}是根据母线的核来写的，每一条都一样 即为u方向的核
knots{2}表达这些母线间的控制关系 即为v方向的核
再填充一条线后的核
pnts(:,:,6)= [2 3 4 5 6 7;
5 5 5 5 5 5;
4 4 4.7 4 4 4];
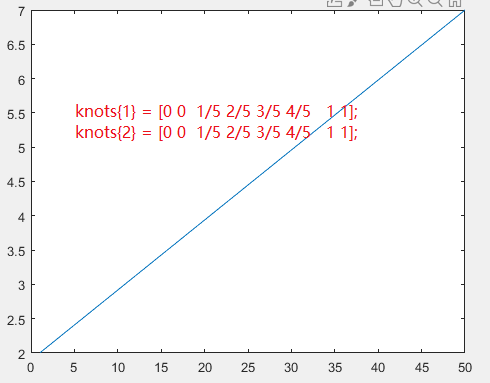
knots{1} = [0 0 1/5 2/5 3/5 4/5 1 1];
knots{2} = [0 0 1/5 2/5 3/5 4/5 1 1];
或者
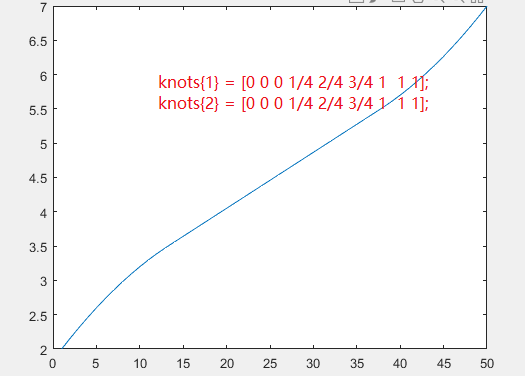
knots{1} = [0 0 0 1/4 2/4 3/4 1 1 1];
knots{2} = [0 0 0 1/4 2/4 3/4 1 1 1];
二重的效果
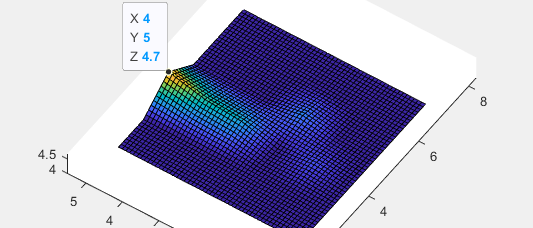
三重的效果
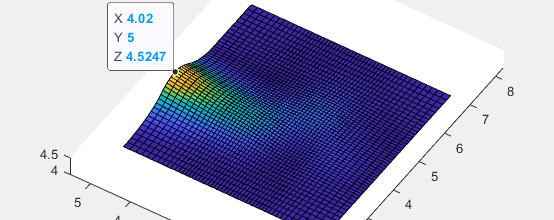
4重的效果
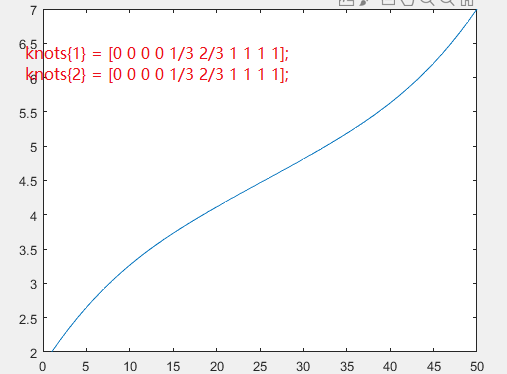
knots{1} = [0 0 0 0 1/3 2/3 1 1 1 1];
knots{2} = [0 0 0 0 1/3 2/3 1 1 1 1];
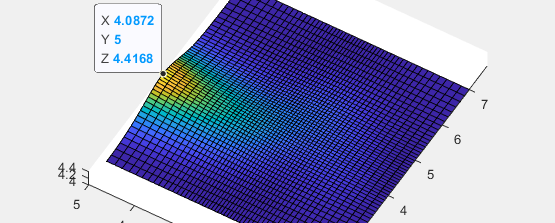
5重的效果
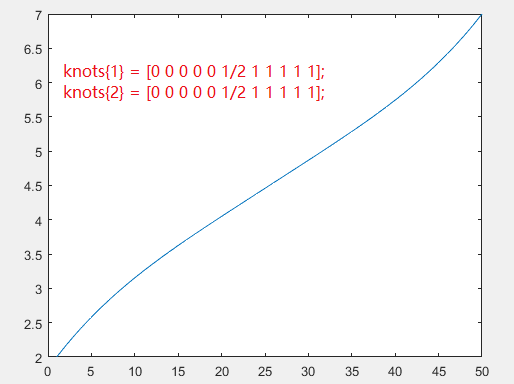
knots{1} = [0 0 0 0 0 1/2 1 1 1 1 1];
knots{2} = [0 0 0 0 0 1/2 1 1 1 1 1];
- 案例----坐标提取
%基于上个案例实现
hold on
pnts(:,:,1) =[2 3 4 5 6 7;
0 0 0 0 0 0;
4 4 4 4 4 4];
pnts(:,:,2) =[2 3 4 5 6 7;
1 1 1 1 1 1;
4 4 4.1 4 4 4];
pnts(:,:,3) =[2 3 4 5 6 7;
2 2 2 2 2 2;
4 4 4 4.2 4 4];
pnts(:,:,4)= [2 3 4 5 6 7;
3 3 3 3 3 3;
4 4 4.3 4 4 4];
pnts(:,:,5)= [2 3 4 5 6 7;
4 4 4 4 4 4;
4 4 4.4 4 4 4];
pnts(:,:,6)= [2 3 4 5 6 7;
5 5 5 5 5 5;
4 4 4.7 4 4 4];
knots{1} = [0 0 1/5 2/5 3/5 4/5 1 1];
knots{2} = [0 0 1/5 2/5 3/5 4/5 1 1];
plane = nrbmak(pnts,knots);
nrbplot(plane, [20 20]);
ut=linspace(0,1,50);%在0~1间等分50份
tt{1}=ut;
tt{2}=[0];
p=nrbeval(plane,tt); %带入求解公式得到对应点的坐标p
plot3(p(1,:),p(2,:),p(3,:),'ro') %画点
hold off
nrbeval可有两种返回形式，
[p,w] = nrbeval(crv,ut)--------曲线
[p,w] = nrbeval(srf,{ut,vt})---曲面
p = nrbeval(crv,ut)------------曲线
p = nrbeval(srf,{ut,vt})-------曲面
p 为NURBS 曲线/面上的点对应的笛卡尔坐标 (x,y,z)。
如果 w 包含在列表中，则点将作为齐次坐标 (wx,wy,wz) 返回。
w为权重
p大小为3*50
**ut与vt**
这两组数据都在0~1之内，大小表达为该点占总长的比例再换算成坐标。
如案例所示，其范围坐标为2~7，
ut=0表示2
ut=1表示7
ut=0.5表示4.5
这个鬼东西(⊙﹏⊙)坑的一批，而且他只在二重情况为等分，其余情况不是等分
横坐标表示为第几个点，纵坐标表示对应返回的x坐标。线性为等分。
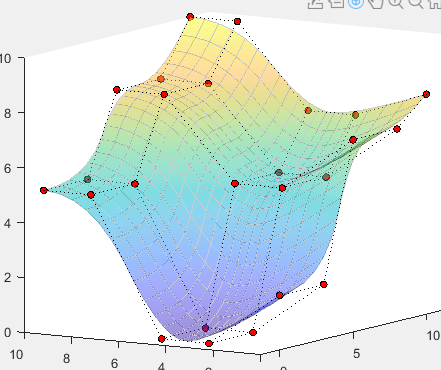
gnurbs 和 nrbplot
在命令行窗口直接输入gnurbs
会自动打开默认实例。
gnurbs与nbrplot参数相同
gnurbs(srf,[xu,xv])
srf nurbs曲线/面
xu，xv 两个方向上用于渲染的分辨率
最后
以上就是体贴月饼为你收集整理的【Matlab-NURBS工具箱简要教程及实例 】添加NURBS工具箱的全部内容，希望文章能够帮你解决【Matlab-NURBS工具箱简要教程及实例 】添加NURBS工具箱所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复