二进制小数的表示

二级制小数分为两大类：1、定点数；2、浮点数。

定点数

定点数：
（1）小数点位置固定不变的数。
（2）定点数有定点整数和定点小数。
（定点整数：小数部分为0；定点小数：整数部分为0）。

定点整数的表示：
规定小数点在最低有效位的后面。
（若为8位来表示，最高位用来表示正负号（即0与1 ），剩下7位为二进制数，小数点在最低位的右边）。

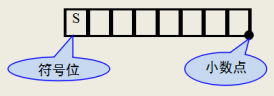
定点小数的表示：
规定小数点在符号位与最高数值位之间。
（若用一个字节表示，最高位为符号位，其他位为二进制数位）

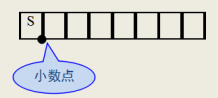
例：将二进制-0.1001001用2个字节存储为定点小数。
解：

（第一个1表示为负号）

浮点数

实数可以表示：
一个纯小数和一个乘幂之积的形式。

浮点数
小数点位置变化的数称为浮点数。
浮点数指数表示：
指数称为“阶码”，小数称为“尾数”。
二进制数的阶码和尾数都用二进制数表示。

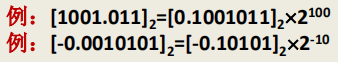
任意二进制浮点数公式：

其中，M为尾数（纯小数部分），整数E为阶码，M与E都带符号。

截断误差（舍入误差）

例：规定用一个字节来记录、存储浮点数，阶符为1位，阶码为2位，尾符为1位，尾数为4位。那么，二进制数10.101存储为浮点数时，尾数由于存储空间不够，导致最右边的1位数据“1”丢失。

这个现象称为截断误差或舍入误差。
二进制浮点数存储时，如果尾数存储空间不够，会导致产生截断误差。可以使用较长的尾数域，减少截断误差。

截断误差的另外一个来源是无穷展开式，也就是在进行数值转换时发生的。
例：十进制数0.8转换为二进制时为：0.11001100…
例：十进制数1/10转换为二进制数时，也会遇到无穷展开式问题。

最后

以上就是清爽画板为你收集整理的二进制小数的表示的全部内容，希望文章能够帮你解决二进制小数的表示所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。