求一个集合的所有子集问题

98 阅读 0 评论 65 点赞

我是靠谱客的博主内向钻石，最近开发中收集的这篇文章主要介绍求一个集合的所有子集问题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

一个包含n个元素的集合,求它的所有子集。比如集合A= {1,2,3}, 它的所有子集是:

{ {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}, @}(@表示空集)。

这种问题一般有两种思路，先说说第一种，递归。递归肯定要基于一个归纳法的思想，这个思想用到了二叉树的遍历，如下图所示:

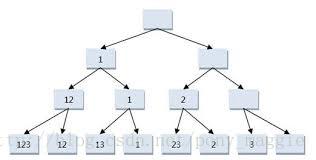
可以这样理解这张图，从集合A的每个元素自身分析，它只有两种状态，或是某个子集的元素，或是不属于任何子集，所以求子集的过程就可以看成对每个元素进行“取舍”的过程。上图中，根结点是初始状态，叶子结点是终结状态，该状态下的8个叶子结点就表示集合A的8个子集。第i层(i=1,2,3…n)表示已对前面i-1层做了取舍，所以这里可以用递归了。整个过程其实就是对二叉树的先序遍历。

根据上面的思想，首先需要一个结构来存储元素，这个”取舍”过程，其实就是在线性结构中的增加和删除操作，很自然考虑用链式的存储结构，所以我们先来实现一个链表：

typedef struct  LNode
{
	int data;
	LNode *next;
}LinkList;

//建立一个链表,你逆向输入n个元素的值
int listCreate(LinkList *srcList, int number)
{
	LinkList *pTemp;
	int i = 0;
	srcList->next = NULL;
	srcList->data = 0;

	for (i = number; i > 0; --i)
	{
		pTemp = (LinkList *)malloc(sizeof(LNode));
		pTemp->data = i+20;//随便赋值
		pTemp->next = srcList->next;
		srcList->next = pTemp;
	}
	return 0;
}

//销毁一个链表
int listDestroy(LinkList *srcList)
{
	if (!srcList || !srcList->next)
	{
		return 0;
	}

	LinkList *p1 = srcList->next;
	LinkList *p2 = p1->next;

	do
	{
		free(p1);
		p1 = p2;
		if (p2 != NULL)
		{
			p2 = p2->next;
		}
	}while (p1);
	return 0;
}

//插入操作
//在strList第nIndex之前插入数据data
//nIndex最小为1
int listInsert(LinkList *srcList, int nIndex, int data)
{
	LinkList *pStart = srcList;
	int j = 0;
	if (nIndex < 1)
	{
		return 0;
	}
	while((pStart) && (j < nIndex-1))
	{
		pStart = pStart->next;
		j++;
	}
	if ((!pStart) || (j > nIndex-1))
	{
		return -1;//出错
	}

	LinkList *temp = (LinkList *)malloc(sizeof(LNode));
	temp->data = data;
	temp->next = pStart->next;
	pStart->next = temp;
	return 0;
}

//删除操作
//strList第nIndex位置的结点删除，并通过data返回被删的元素的值
//通常情况下返回的这个值是用不到的，不过这里也保留备用
int listDelete(LinkList *srcList, int nIndex, int *data)
{
	LinkList *pStart = srcList;
	int j = 0;
	if (nIndex < 1)
	{
		return 0;
	}

	while((pStart) && (j < nIndex-1))
	{
		pStart = pStart->next;
		j++;
	}
	if ((!pStart) || (j > nIndex-1))
	{
		return -1;//出错
	}
	LinkList *pTemp = pStart->next;
	pStart->next = pTemp->next;
	*data = pTemp->data;
	free(pTemp);

}

有了这个链表，递归算法实现起来就很容易了:

//求冥集，nArray是存放n个元素的数组
//首次调用i传1,表示已对前面i-1个元素做了处理
void GetPowerSet(int nArray[], int nLength, int i, LinkList *outPut)
{
	int k = 0;
	int nTemp = 0;
	if (i >= nLength)
	{
		printList(*outPut);
	}
	else
	{
		k = listLength(outPut);
		listInsert(outPut, k+1, nArray[i]);
		GetPowerSet(nArray, nLength, i+1, outPut);
		listDelete(outPut, k+1, &nTemp);
		GetPowerSet(nArray, nLength, i+1, outPut);
	}

}

还有一种思想比较巧妙，可以叫按位对应法。如集合A={a,b,c},对于任意一个元素，在每个子集中，要么存在，要么不存在。

映射为子集：

(a,b,c)

(1,1,1)->(a,b,c)

(1,1,0)->(a,b)

(1,0,1)->(a,c)

(1,0,0)->(a)

(0,1,1)->(b,c)

(0,1,0)->(b)

(0,0,1)->(c)

(0,0,0)->@(@表示空集)

观察以上规律，与计算机中数据存储方式相似，故可以通过一个整型数与集合映射...000 ~ 111...111（表示有，表示无，反之亦可），通过该整型数逐次增可遍历获取所有的数，即获取集合的相应子集。

实现起来很容易:

void GetPowerSet2(int nArray[], int nLength)
{
	int mark = 0;
	int i = 0;
	int nStart = 0;
	int nEnd = (1 << nLength) -1;
	bool bNullSet = false;

	for (mark = nStart; mark <= nEnd; mark++)
	{
		bNullSet = true;
		for (i = 0; i < nLength; i++)
		{
			if (((1<<i)&mark) != 0) //该位有元素输出
			{
				bNullSet = false;
				printf("%dt", nArray[i]);
			}
		}
		if (bNullSet) //空集合
		{
			printf("@t");
		}
		printf("n");
	}
}

分析代码可以得出它的复杂度是O(n*2^n)。

代码下载地址:

https://github.com/pony-maggie/PowerSetDemo

或

http://download.csdn.net/detail/pony_maggie/7499161