本博英文版参见
[English Version]

1 创建一个函数

注：一般用于比较复杂的映射关系

在MATLAB中创建一个函数需要创建一个脚本(Script)，单击左上角“New Script”创建一个m文件，

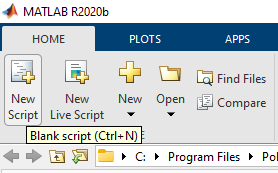
系统默认文件名为“Untitled*”，星号“*”表示有内容未保存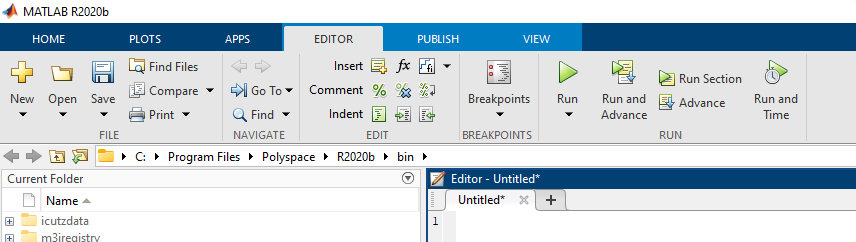定义函数需以function 开头，end结尾，在MATLAB中会自动显示该函数表达式的结构

注：function 和end之间描述映射关系的部分注意应以分号;结尾

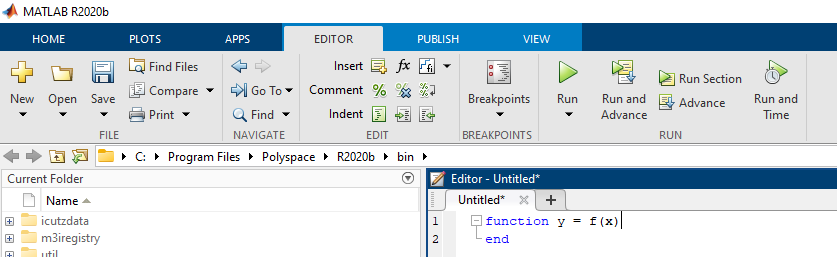
注：文件名需要和映射名称一致，否则会报形如
Function name 'f' is known to MATLAB by its file name:'Untitled'.
的错误

2 基本初等函数

2.1 三角函数和反三角函数

注：使用弧度制时，π在MATLAB中为pi

2.1.1. 三角函数（弧度制）

正弦y = sin(x);
余弦y = cos(x);
正切y = tan(x);
余切y = cot(x);
正割y = sec(x);
余割y = csc(x);

2.1.2 反三角函数（弧度制）

反正弦y = asin(x);
反余弦y = acos(x);
反正切y = atan(x);
四象限反正切y = atan2(x);
反余切y = acot(x);
反正割y = asec(x);
反余割y = acsc(x);

2.1.3 三角函数（角度制）

正弦y = sind(x);
余弦y = cosd(x);
正切y = tand(x);
余切y = cotd(x);
正割y = secd(x);
余割y = cscd(x);

2.1.4 反三角函数（角度制）

反正弦y = asind(x);
反余弦y = acosd(x);
反正切y = atand(x);
反余切y = acotd(x);
反正割y = asecd(x);
反余割y = acscd(x);

2.1.5 双曲函数

双曲正弦y = sinh(x);
双曲余弦y = cosh(x);
双曲正切y = tanh(x);
双曲余切y = coth(x);
双曲正割y = sech(x);
双曲余割y = csch(x);

2.1.6 反双曲函数

反双曲正弦y = asinh(x);
反双曲余弦y = acosh(x);
反双曲正切y = atanh(x);
反双曲余切y = acoth(x);
反双曲正割y = asech(x);
反双曲余割y = acsch(x);

2.2 其他函数

常函数y = a;，其中a为读者给定的值
幂函数y = x^b;，其中b为读者给定的指数
对数函数y = logc(x);，其中c为读者给定的底数，如若不写，则默认为自然对数y = log(x);
指数函数y = d^x;，其中d为读者给定的底数

3 分段函数

现有一复杂的分段函数
$$f(x)=\{\begin{array}{cc}& \\ \frac{1}{11}& x>0.015\\ & \\ \frac{3-800\cdot (x-0.0125)}{11}& 0.0125<x\le 0.015\\ & \\ \frac{5-800\cdot (x-0.01)}{11}& 0.01<x\le 0.0125\\ & \\ \frac{7-800\cdot (x-0.0075)}{11}& 0.0075<x\le 0.01\\ & \\ \frac{11-800\cdot (x-0.005)}{11}& x\le 0.0075\end{array}$$
如何实现定义呢？以下给出两种方法供读者参考。

3.1 条件语句

多分支if语句

function y=f(x)

if x>0.015
y=1/11;

elseif (x>0.0125)& (x<=0.015)
y=3/11-800/11* (x-0.0125);

elseif (x>0.01)&(x<=0.0125)
y=5/11-800/11* (x-0.01);

elseif (x>0.0075)&(x<=0.01)
y=7/11-800/11*(x-0.0075);

else
y=1-800/11*(x-0.005);

end

3.2 逻辑运算

MATLAB在进行与（代码&）或（代码|）等逻辑运算后会返回一个布尔值0或1，我们可以利用这个特性用一行长代码予以解决。

function y=f(x)
 y=(1-800/11*(x-0.005)).*(x<=0.005)+(7-800/11*(x-0.0075)).*(x>0.0075&x<=0.01)+(5-800/11*(x-0.01)).*(x>0.01&x<=0.0125)+(3-800/11*(x-0.0125)/0.0025).*(x>0.0125&x<=0.015)+(1/9).*(x>0.015);
end

最后

以上就是甜甜白云为你收集整理的如何优雅地在MATLAB中敲出数学公式？(Ⅰ)1 创建一个函数2 基本初等函数3 分段函数的全部内容，希望文章能够帮你解决如何优雅地在MATLAB中敲出数学公式？(Ⅰ)1 创建一个函数2 基本初等函数3 分段函数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。