我是靠谱客的博主 昏睡水杯，最近开发中收集的这篇文章主要介绍【Eigen】基本和常用函数简介找不到头文件Eigen 中矩阵的定义Eigen 中矩阵的使用方法Eigen 中常用矩阵生成Eigen 中矩阵分块Eigen 中矩阵元素交换Eigen 中矩阵转置Eigen 中矩阵乘积Eigen 中矩阵元素操作Eigen 中矩阵化简Eigen 中矩阵点乘Eigen 中矩阵类型转换Eigen 中求解线性方程组 Ax = bEigen 中矩阵特征值Eigen中Matrix的行优先与列优先Eigen使用注意事项Eigen中的noalias()和eval()解决矩阵运算中的，觉得挺不错的，现在分享给大家，希望可以做个参考。
概述
文章目录
- 简介
- 找不到头文件
- Eigen 中矩阵的定义
- Eigen 中矩阵的使用方法
- Eigen 中常用矩阵生成
- Eigen 中矩阵分块
- Eigen 中矩阵元素交换
- Eigen 中矩阵转置
- Eigen 中矩阵乘积
- Eigen 中矩阵元素操作
- Eigen 中矩阵化简
- Eigen 中矩阵点乘
- Eigen 中矩阵类型转换
- Eigen 中求解线性方程组 Ax = b
- Eigen 中矩阵特征值
- Eigen中Matrix的行优先与列优先
- Eigen使用注意事项
- Eigen中的`noalias()`和`eval()`解决矩阵运算中的混淆问题
- Eigen实现四元数、欧拉角、旋转矩阵、旋转向量之间的转换
- 1 旋转向量
- 2 旋转矩阵
- 3 欧拉角
- 4 四元数
- 5 齐次欧式变换
简介
- Eigen是一个C++语言中的开源的模板库，支持线性代数的运算，包括向量运算，矩阵运算，数值分析等相关算法。因为eigen只包含头文件，所以使用的话不需要进行编译
Eigen —— 参考指南
Eigen库学习教程(全)
Eigen教程:1 Eigen简介和矩阵常见操作
Eigen学习教程(一)
Eigen学习教程(二)
Eigen学习教程(三)
Eigen学习教程(四)
Eigen教程-Github
Eigen库使用笔记 — 一个工程师的存档点
模块与头文件
| 模块 | 头文件 | 内容 |
|---|---|---|
| Core | #include <Eigen/Core> | 矩阵和数组 (向量) 类 (Matrix, Array)，基本的线性代数运算和数组操作 |
| Geometry | #include <Eigen/Geometry> | 变换，平移，缩放，2D 旋转和 3D 旋转 (包括四元数和角轴) |
| LU | #include <Eigen/LU> | 使用求解器进行求逆，行列式，LU 分解操作 |
| Cholesky | #include <Eigen/Cholesky> | 使用求解器进行 LLT, LT, Cholesky 分解 |
| Householder | #include <Eigen/Householder> | Householder 变换；被用作几个线性代数模块 |
| SVD | #include <Eigen/Cholesky> | SVD 分解与最小二乘求解器 |
| QR | #include <Eigen/QR> | QR 分解 |
| Eigenvalues | #include <EIgen/Eigenvalues> | 特征值，特征向量分解 |
| Sparse | #include <Eigen/Sparse> | 稀疏矩阵存储以及相关的基本线性代数 |
| Dense | #include <Eigen/Dense> | 包括 Core, Geometry, LU, Cholesky, SVD, QR, Eigenvalues 的头文件 |
| Eigen | #include <Eigen/Eigen> | 包括 Dense 和 Sparse 的头文件 |
- Dense模块整合了一系列模块，Eigen模块整合了所有模块。一般，
#include <Eigen/Dense>就够了
找不到头文件
1、原因分析
- Eigen被默认安装到了usr/include/eigen3里了（系统默认的路径），导致编译器在include目录下找不到Eigen，从而导致错误。
2、解决办法
- 第一种
将#include<Eigen/Core> 改写成 #include<eigen3/Eigen/Core>
将#include<Eigen/Dense> 改写成 #include<eigen3/Eigen/Dense>
-
第二种
在CMakeLists中添加include_directories(“/usr/include/eigen3”)
因为eigen3被默认安装到了usr/include里了（系统默认的路径），在很多程序中include时经常使用#include<Eigen/Dense>而不是使用#include<eigen3/Eigen/Dense>所以要做一下处理，否则有些程序在编译时找不到Eigen/Dense而报错。上面指令将usr/include/eigen3文件夹中的Eigen文件递归的复制到上一层文件（直接放到/usr/include中，否则系统无法默认搜索到----->此时只能在CMakeLists.txt用include_libraries（绝对路径了））
sudo cp -r /usr/include/eigen3/Eigen /usr/include
- matlab中的下标都是从1开始的，未来可能调整从0开始，目的是为了兼容第三方语言，许多编程语言下标都是从0开始的。
Eigen 中矩阵的定义
#include <Eigen/Dense> // 基本函数只需要包含这个头文件
Matrix<double, 3, 3> A; // 固定了行数和列数的矩阵和Matrix3d一致.
Matrix<double, 3, Dynamic> B; // 固定行数.
Matrix<double, Dynamic, Dynamic> C; // 和MatrixXd一致.
Matrix<double, 3, 3, RowMajor> E; // 按行存储; 默认按列存储.
Matrix3f P, Q, R; // 3x3 float 矩阵.
Vector3f x, y, z; // 3x1 float 列向量.
RowVector3f a, b, c; // 1x3 float 行向量.
VectorXd v; // 动态长度double型列向量
// Eigen // Matlab // comments
x.size() // length(x) // 向量的长度
C.rows() // size(C,1) // 矩阵的行数
C.cols() // size(C,2) // 矩阵的列数
x(i) // x(i+1) // 访问向量元素（Matlab的下标从1开始计数）
C(i,j) // C(i+1,j+1) // 访问矩阵元素
Eigen 中矩阵的使用方法
A.resize(4, 4); // 如果越界触发运行时错误.
B.resize(4, 9); // 如果越界触发运行时错误.
A.resize(3, 3); // Ok; 没有越界.
B.resize(3, 9); // Ok; 没有越界.
A << 1, 2, 3, // 初始化A，元素也可以是矩阵，先按列堆叠，再按行堆叠。（从左到右，从上到下）
4, 5, 6,
7, 8, 9;
B << A, A, A; // B 是3个A水平排列
A.fill(10); // 将A的所有元素填充为10
Eigen 中常用矩阵生成
// Eigen // Matlab 注释
MatrixXd::Identity(rows,cols) // eye(rows,cols) //单位矩阵
C.setIdentity(rows,cols) // C = eye(rows,cols) //单位矩阵
MatrixXd::Zero(rows,cols) // zeros(rows,cols) //全零矩阵
C.setZero(rows,cols) // C = zeros(rows,cols) //全零矩阵
MatrixXd::Ones(rows,cols) // ones(rows,cols) //全一矩阵
C.setOnes(rows,cols) // C = ones(rows,cols) //全一矩阵
MatrixXd::Random(rows,cols) // rand(rows,cols)*2-1 //MatrixXd::Random 返回范围为(-1, 1)的均匀分布的随机数
C.setRandom(rows,cols) // C = rand(rows,cols)*2-1 //返回范围为(-1, 1)的均匀分布的随机数
VectorXd::LinSpaced(size,low,high) // linspace(low,high,size)' //返回size个等差数列，第一个数为low，最后一个数为high
v.setLinSpaced(size,low,high) // v = linspace(low,high,size)' //返回size个等差数列，第一个数为low，最后一个数为high
VectorXi::LinSpaced(((hi-low)/step)+1, // low:step:hi //以step为步长的等差数列。((hi-low)/step)+1为个数
low,low+step*(size-1)) //
Eigen 中矩阵分块
// Matrix 切片和块。下面列出的所有表达式都是可读/写的。
// 使用模板参数更快（如第2个）。注意：Matlab是的下标是从1开始的。
// Eigen // Matlab // 注释
x.head(n) // x(1:n) //前n个元素
x.head<n>() // x(1:n) //前n个元素
x.tail(n) // x(end - n + 1: end) //倒数n个元素
x.tail<n>() // x(end - n + 1: end) //倒数n个元素
x.segment(i, n) // x(i+1 : i+n) //切片
x.segment<n>(i) // x(i+1 : i+n) //切片
P.block(i, j, rows, cols) // P(i+1 : i+rows, j+1 : j+cols) //块
P.block<rows, cols>(i, j) // P(i+1 : i+rows, j+1 : j+cols) //块
P.row(i) // P(i+1, :) //第i行
P.col(j) // P(:, j+1) //第j列
P.leftCols<cols>() // P(:, 1:cols) //前cols列
P.leftCols(cols) // P(:, 1:cols) //前cols列
P.middleCols<cols>(j) // P(:, j+1:j+cols) //中间cols列
P.middleCols(j, cols) // P(:, j+1:j+cols) //中间cols列
P.rightCols<cols>() // P(:, end-cols+1:end) //后cols列
P.rightCols(cols) // P(:, end-cols+1:end) //后cols列
P.topRows<rows>() // P(1:rows, :) //前rows行
P.topRows(rows) // P(1:rows, :) //前rows行
P.middleRows<rows>(i) // P(i+1:i+rows, :) //中间rows行
P.middleRows(i, rows) // P(i+1:i+rows, :) //中间rows行
P.bottomRows<rows>() // P(end-rows+1:end, :) //最后rows行
P.bottomRows(rows) // P(end-rows+1:end, :) //最后rows行
P.topLeftCorner(rows, cols) // P(1:rows, 1:cols) //左上角块
P.topRightCorner(rows, cols) // P(1:rows, end-cols+1:end) //右上角块
P.bottomLeftCorner(rows, cols) // P(end-rows+1:end, 1:cols) //左下角块
P.bottomRightCorner(rows, cols) // P(end-rows+1:end, end-cols+1:end) //右下角块
P.topLeftCorner<rows,cols>() // P(1:rows, 1:cols) //左上角块
P.topRightCorner<rows,cols>() // P(1:rows, end-cols+1:end) //右上角块
P.bottomLeftCorner<rows,cols>() // P(end-rows+1:end, 1:cols) //左下角块
P.bottomRightCorner<rows,cols>() // P(end-rows+1:end, end-cols+1:end) //右下角块
Eigen 中矩阵元素交换
// 特别说明：Eigen的交换函数进行了高度优化
// Eigen // Matlab
R.row(i) = P.col(j); // R(i, :) = P(:, j)
R.col(j1).swap(mat1.col(j2)); // R(:, [j1 j2]) = R(:, [j2, j1]) //交换列
Eigen 中矩阵转置
// Views, transpose, etc;
// Eigen // Matlab
R.adjoint() // R' // 共轭转置
R.transpose() // R.' or conj(R') // 可读/写 转置
R.diagonal() // diag(R) // 可读/写 获取对角元素
x.asDiagonal() // diag(x) // diag(x)对角阵(通过x中元素作为对角元素（构建对角矩阵）这里x必须为VectorXX类型不能为矩阵)
R.transpose().colwise().reverse() // rot90(R) // 可读/写 逆时针旋转90度
R.rowwise().reverse() // fliplr(R) // 水平翻转
R.colwise().reverse() // flipud(R) // 垂直翻转
R.replicate(i,j) // repmat(P,i,j) // 复制矩阵，垂直复制i个，水平复制j个
Eigen 中矩阵乘积
// 四则运算，和Matlab相同。但Matlab中不能使用*=这样的赋值运算符
// 矩阵 - 向量 矩阵 - 矩阵 矩阵 - 标量
y = M*x; R = P*Q; R = P*s;
a = b*M; R = P - Q; R = s*P;
a *= M; R = P + Q; R = P/s;
R *= Q; R = s*P;
R += Q; R *= s;
R -= Q; R /= s;
Eigen 中矩阵元素操作
// 逐元素操作Vectorized operations on each element independently
// Eigen // Matlab //注释
R = P.cwiseProduct(Q); // R = P .* Q //逐元素乘法
R = P.array() * s.array(); // R = P .* s //逐元素乘法（s为标量）
R = P.cwiseQuotient(Q); // R = P ./ Q //逐元素除法
R = P.array() / Q.array(); // R = P ./ Q //逐元素除法
R = P.array() + s.array(); // R = P + s //逐元素加法（s为标量）
R = P.array() - s.array(); // R = P - s //逐元素减法（s为标量）
R.array() += s; // R = R + s //逐元素加法（s为标量）
R.array() -= s; // R = R - s //逐元素减法（s为标量）
R.array() < Q.array(); // R < Q //逐元素比较运算
R.array() <= Q.array(); // R <= Q //逐元素比较运算
R.cwiseInverse(); // 1 ./ P //逐元素取倒数
R.array().inverse(); // 1 ./ P //逐元素取倒数
R.array().sin() // sin(P) //逐元素计算正弦函数
R.array().cos() // cos(P) //逐元素计算余弦函数
R.array().pow(s) // P .^ s //逐元素计算幂函数
R.array().square() // P .^ 2 //逐元素计算平方
R.array().cube() // P .^ 3 //逐元素计算立方
R.cwiseSqrt() // sqrt(P) //逐元素计算平方根
R.array().sqrt() // sqrt(P) //逐元素计算平方根
R.array().exp() // exp(P) //逐元素计算指数函数
R.array().log() // log(P) //逐元素计算对数函数
R.cwiseMax(P) // max(R, P) //逐元素计算R和P的最大值
R.array().max(P.array()) // max(R, P) //逐元素计算R和P的最大值
R.cwiseMin(P) // min(R, P) //逐元素计算R和P的最小值
R.array().min(P.array()) // min(R, P) //逐元素计算R和P的最小值
R.cwiseAbs(P) // abs(P) //逐元素计算R和P的绝对值
R.array().abs() // abs(P) //逐元素计算绝对值
R.cwiseAbs2() // abs(P.^2) //逐元素计算平方
R.array().abs2() // abs(P.^2) //逐元素计算平方
(R.array() < s).select(P,Q); // (R < s ? P : Q) //根据R的元素值是否小于s，选择P和Q的对应元素
R = (Q.array()==0).select(P,A) // R(Q==0) = P(Q==0) R(Q!=0) = P(Q!=0) //根据Q中元素等于零的位置选择P中元素
R = P.unaryExpr(ptr_fun(func)) // R = arrayfun(func, P) // 对P中的每个元素应用func函数
Eigen 中矩阵化简
// Reductions.
int r, c;
// Eigen // Matlab //注释
R.minCoeff() // min(R(:)) //最小值
R.maxCoeff() // max(R(:)) //最大值
s = R.minCoeff(&r, &c) // [s, i] = min(R(:)); [r, c] = ind2sub(size(R), i); //计算最小值和它的位置
s = R.maxCoeff(&r, &c) // [s, i] = max(R(:)); [r, c] = ind2sub(size(R), i); //计算最大值和它的位置
R.sum() // sum(R(:)) //求和（所有元素）
R.colwise().sum() // sum(R) //按列求和
R.rowwise().sum() // sum(R, 2) or sum(R')' //按行求和
R.prod() // prod(R(:)) //累积
R.colwise().prod() // prod(R) //按列累积
R.rowwise().prod() // prod(R, 2) or prod(R')' //按行累积
R.trace() // trace(R) //迹
R.all() // all(R(:)) //是否所有元素都非零
R.colwise().all() // all(R) //按列判断，是否该列所有元素都非零
R.rowwise().all() // all(R, 2) //按行判断，是否该行所有元素都非零
R.any() // any(R(:)) //是否有元素非零
R.colwise().any() // any(R) //按列判断，是否该列有元素都非零
R.rowwise().any() // any(R, 2) //按行判断，是否该行有元素都非零
Eigen 中矩阵点乘
// 点积，范数等
// Eigen // Matlab // 注释
x.norm() // norm(x) //范数（注意：Eigen中没有norm(R)）
x.squaredNorm() // dot(x, x) //平方和（注意：对于复数而言，不等价）
x.dot(y) // dot(x, y) //点积
x.cross(y) // cross(x, y) //交叉积，需要头文件 #include <Eigen/Geometry>
Eigen 中矩阵类型转换
// 类型转换
// Eigen // Matlab // 注释
A.cast<double>(); // double(A) //变成双精度类型
A.cast<float>(); // single(A) //变成单精度类型
A.cast<int>(); // int32(A) //编程整型
A.real(); // real(A) //实部
A.imag(); // imag(A) //虚部
// 如果变换前后的类型相同，不做任何事情。
// 注意：Eigen中，绝大多数的涉及多个操作数的运算都要求操作数具有相同的类型
MatrixXf F = MatrixXf::Zero(3,3);
A += F; // 非法。Matlab中允许。（单精度+双精度）
A += F.cast<double>(); // 将F转换成double，并累加。（一般都是在使用时临时转换）
// Eigen 可以将已存储数据的缓存 映射成 Eigen矩阵
float array[3];
Vector3f::Map(array).fill(10); // create a temporary Map over array and sets entries to 10
int data[4] = {1, 2, 3, 4};
Matrix2i mat2x2(data); // 将 data 复制到 mat2x2
Matrix2i::Map(data) = 2*mat2x2; // 使用 2*mat2x2 覆写data的元素
MatrixXi::Map(data, 2, 2) += mat2x2; // 将 mat2x2 加到 data的元素上 (当编译时不知道大小时，可选语法)
Eigen 中求解线性方程组 Ax = b
// Solve Ax = b. Result stored in x. Matlab: x = A b.
x = A.ldlt().solve(b)); // #include <Eigen/Cholesky>LDLT分解法实际上是Cholesky分解法的改进
x = A.llt() .solve(b)); // A sym. p.d. #include <Eigen/Cholesky>
x = A.lu() .solve(b)); // Stable and fast. #include <Eigen/LU>
x = A.qr() .solve(b)); // No pivoting. #include <Eigen/QR>
x = A.svd() .solve(b)); // Stable, slowest. #include <Eigen/SVD>
// .ldlt() -> .matrixL() and .matrixD()
// .llt() -> .matrixL()
// .lu() -> .matrixL() and .matrixU()
// .qr() -> .matrixQ() and .matrixR()
// .svd() -> .matrixU(), .singularValues(), and .matrixV()
Eigen 中矩阵特征值
// Eigen // Matlab
A.eigenvalues(); // eig(A);特征值
EigenSolver<Matrix3d> eig(A); // [vec val] = eig(A)
eig.eigenvalues(); // diag(val)与前边的是一样的结果
eig.eigenvectors(); // vec 特征值对应的特征向量
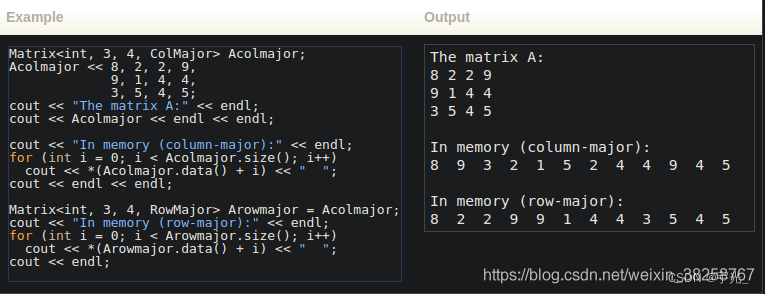
Eigen中Matrix的行优先与列优先
在Eigen中矩阵的存储默认是列优先的，但也可以设置为行优先：
Matrix<double, 6, Dynamic, RowMajor> mat;
行优先与列优先在使用上没有区别，但是如果按列访问，列优先因为存储位置相邻会比行优先更快些。
Eigen使用注意事项
- 结构体或者类包含定长的Eigen数据结构，需要在结构体或者类内添加
EIGEN_MAKE_ALIGNED_OPERATOR_NEW，具体见 Eigen 官网
class Foo
{
//...
Eigen::Vector4d v;
//...
};
//...
Foo *foo = new Foo;
改为：
class Foo
{
...
Eigen::Vector4d v;
...
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
};
...
Foo *foo = new Foo;
- STL容器（如
std::vector, std::map）包含Eigen数据结构，需要添加Eigen::aligned_allocator，具体见Eigen 官网
std::map<int, Eigen::Vector4d>
改为：
std::map<int, Eigen::Vector4d, std::less<int>, Eigen::aligned_allocator<std::pair<const int, Eigen::Vector4d> > >
- 函数传递Eigen构数据结构，需要传引用，具体见Eigen 官网
void my_function(Eigen::Vector2d v);
改为：
void my_function(const Eigen::Vector2d& v);
Eigen中的noalias()和eval()解决矩阵运算中的混淆问题
Eigen中的noalias()： 解决矩阵运算的混淆问题
混淆问题的解决办法
- compnent级别的操作不用考虑混淆。
- 矩阵相乘，Eigen默认会解决混淆问题，如果你确定不会出现混淆，可以使用
noalias()来提效。 - 混淆出现时，可以用
eval()和xxxInPlace()函数解决。
Eigen实现四元数、欧拉角、旋转矩阵、旋转向量之间的转换
- 使用Eigen实现四元数、欧拉角、旋转矩阵、旋转向量之间的转换1
- 使用Eigen实现四元数、欧拉角、旋转矩阵、旋转向量之间的转换2
- 处理2D、3D旋转、射影以及仿射等变换
Vector3.normalized的特点是当前向量是不改变的并且返回一个新的规范化的向量；Vector3.Normalize的特点是改变当前向量，也就是当前向量长度是1
1 旋转向量
- 初始化旋转向量
//旋转角为alpha(顺时针)，旋转轴为(x,y,z)
Eigen::AngleAxisd rotation_vector(alpha,Vector3d(x,y,z))
Eigen::AngleAxisd yawAngle(alpha,Vector3d::UnitZ());
- 旋转向量转旋转矩阵
Eigen::Matrix3d rotation_matrix;
rotation_matrix = rotation_vector.matrix();
Eigen::Matrix3d rotation_matrix;
rotation_matrix = rotation_vector.toRotationMatrix();
- 旋转向量转欧拉角(xyz，即RPY)
Eigen::Vector3d eulerAngle = rotation_vector.matrix().eulerAngles(0,1,2);
- 旋转向量转四元数
Eigen::Quaterniond quaternion(rotation_vector);
Eigen::Quaterniond quaternion;
quaternion = rotation_vector;
2 旋转矩阵
- 初始化旋转矩阵
Eigen::Matrix3d rotation_matrix;
rotation_matrix << x_00, x_01, x_02, x_10, x_11, x_12, x_20, x_21, x_22;
- 旋转矩阵转旋转向量
Eigen::AngleAxisd rotation_vector(rotation_matrix);
Eigen::AngleAxisd rotation_vector;
rotation_vector = rotation_matrix;
Eigen::AngleAxisd rotation_vector;
rotation_vector.fromRotationMatrix(rotation_matrix);
- 旋转矩阵转欧拉角(xyz，即RPY)
Eigen::Vector3d eulerAngle = rotation_matrix.eulerAngles(0,1,2);
- 旋转矩阵转四元数
Eigen::Quaterniond quaternion(rotation_matrix);
Eigen::Quaterniond quaternion;
quaternion = rotation_matrix;
3 欧拉角
- 初始化欧拉角(xyz，即RPY)
Eigen::Vector3d eulerAngle(roll,pitch,yaw);
- 欧拉角转旋转向量
Eigen::AngleAxisd rollAngle(AngleAxisd(eulerAngle(0),Vector3d::UnitX()));
Eigen::AngleAxisd pitchAngle(AngleAxisd(eulerAngle(1),Vector3d::UnitY()));
Eigen::AngleAxisd yawAngle(AngleAxisd(eulerAngle(2),Vector3d::UnitZ()));
Eigen::AngleAxisd rotation_vector;
rotation_vector = yawAngle*pitchAngle*rollAngle;
- 欧拉角转旋转矩阵
Eigen::AngleAxisd rollAngle(AngleAxisd(eulerAngle(0),Vector3d::UnitX()));
Eigen::AngleAxisd pitchAngle(AngleAxisd(eulerAngle(1),Vector3d::UnitY()));
Eigen::AngleAxisd yawAngle(AngleAxisd(eulerAngle(2),Vector3d::UnitZ()));
Eigen::Matrix3d rotation_matrix;
rotation_matrix = yawAngle*pitchAngle*rollAngle;
- 欧拉角转四元数
Eigen::AngleAxisd rollAngle(AngleAxisd(eulerAngle(0),Vector3d::UnitX()));
Eigen::AngleAxisd pitchAngle(AngleAxisd(eulerAngle(1),Vector3d::UnitY()));
Eigen::AngleAxisd yawAngle(AngleAxisd(eulerAngle(2),Vector3d::UnitZ()));
Eigen::Quaterniond quaternion;
quaternion = yawAngle*pitchAngle*rollAngle;
4 四元数
- 初始化四元数
Eigen::Quaterniond quaternion(w,x,y,z);
- 四元数转旋转向量
Eigen::AngleAxisd rotation_vector(quaternion);
Eigen::AngleAxisd rotation_vector;
rotation_vector = quaternion;
- 四元数转旋转矩阵
Eigen::Matrix3d rotation_matrix;
rotation_matrix = quaternion.matrix();
Eigen::Matrix3d rotation_matrix;
rotation_matrix = quaternion.toRotationMatrix();
- 四元数转欧拉角(xyz，即RPY)
Eigen::Vector3d eulerAngle = quaternion.matrix().eulerAngles(0,1,2);
5 齐次欧式变换
Isometry3d T = Isometry3d::Identity();
T.rotate(rotation_vector1);
T.pretranslate(t);
cout<<"齐次欧式变换：n"<<T.matrix()<<endl;
最后
以上就是昏睡水杯为你收集整理的【Eigen】基本和常用函数简介找不到头文件Eigen 中矩阵的定义Eigen 中矩阵的使用方法Eigen 中常用矩阵生成Eigen 中矩阵分块Eigen 中矩阵元素交换Eigen 中矩阵转置Eigen 中矩阵乘积Eigen 中矩阵元素操作Eigen 中矩阵化简Eigen 中矩阵点乘Eigen 中矩阵类型转换Eigen 中求解线性方程组 Ax = bEigen 中矩阵特征值Eigen中Matrix的行优先与列优先Eigen使用注意事项Eigen中的noalias()和eval()解决矩阵运算中的的全部内容，希望文章能够帮你解决【Eigen】基本和常用函数简介找不到头文件Eigen 中矩阵的定义Eigen 中矩阵的使用方法Eigen 中常用矩阵生成Eigen 中矩阵分块Eigen 中矩阵元素交换Eigen 中矩阵转置Eigen 中矩阵乘积Eigen 中矩阵元素操作Eigen 中矩阵化简Eigen 中矩阵点乘Eigen 中矩阵类型转换Eigen 中求解线性方程组 Ax = bEigen 中矩阵特征值Eigen中Matrix的行优先与列优先Eigen使用注意事项Eigen中的noalias()和eval()解决矩阵运算中的所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复