算法设计方法

蛮力法

把所有的可能都算一遍，不考虑优化之类的。简单，低效率

算法设计过程：计算所有的可能性即可
典型算法：冒泡排序
例子：给定一组数字和目标值，找出两个数字相加等于目标值, 返回索引。
思路：双重循环，找到所有两个数字的组合相加 == 目标值

var twoSum = function(nums, target) {
    for (let i=0; i<nums.length; i++) {
        for (let j=i+1; j<nums.length; j++) {
            if (nums[i]+nums[j] == target) {
                return [i,j]
            }
        }
    }
};
twoSum([7,2,9,10],9) // [0,1]
// 时间复杂度：O(n^2)
// 空间复杂度：O(1)

减治法

减少计算量
算法设计过程: 把对结果没有用处的计算去掉
典型算法：二分法
例子：在一个有序数组中，查找目标值，返回索引

var search = function(nums, target) {
    let start = 0;
    let end = nums.length-1;
    while (start<=end) {
        let mid = Math.floor((start+end)/2)
        if (nums[mid] == target) {
            return mid;
        } else if (target > nums[mid]) { // 目标在右边
            start = mid+1;
        } else { // 目标在左边
            end = mid-1;
        }
    }
    return -1;
};
// 算法分析：每次缩小一半的查找范围
// 时间复杂度：O(logn)
// 空间复杂度：O(1)

分治法

把问题分解成子问题，再合并子问题的解。通常和递归一起使用
算法设计过程:

1. 写出处理子问题的步骤
2. 合并子问题的解
3. 分解子问题

典型算法：快速排序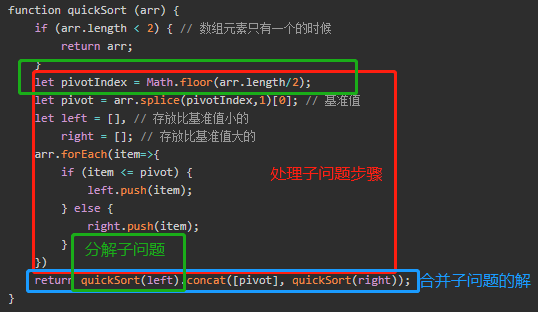

变治法

              更简单的实例
问题的实例 ->  有现成的算法可使用的问题实例
			  另一种表现

算法设计过程： 找到该问题的另一种问题表现方式，高效解决当前问题。
例子： 如果给定的数组有重复元素，返回true, 否则否会false。
使用蛮力法，时间复杂度为O(n^2/2)

        function search(arr) {
            for (let i=0; i<arr.length; i++) {
                for (let j=i+1; j<arr.length; j++) {
                    count++;
                    if (arr[i] == arr[j]) {
                        return true;
                    }
                }
            }
            return false;
        }

排序法：如果数组是有序，那么我们只需判断每个元素的后一个是否相等就可以了，时间复杂度为O(nlogn)

        function search(arr) {
            arr.sort((a,b)=>{count++; return a-b})
            for (let i=1; i<arr.length; i++) {
                count++;
                if (arr[i-1] == arr[i]) {
                    return true;
                }
            }
            return false;
        }

计数法：如果我们知道每个元素的数量，只需要判断它们的数量是不是1就可以了。时间复杂度为O(n)

        function search(arr) {
            let map = {};
            for (let i=0; i<arr.length; i++) {
                let num = arr[i];
                count++;
                if (map[num]) {
                    return true
                } else {
                    map[num] = 1;
                };
            }
            return false;
        }

时空权衡

时间换空间：用低效率换来少的空间使用
例子：引用变治法中的例子，用蛮力法解决，时间复杂度O(n^2/2) 空间复杂度O(1)
空间换时间：用高效率换来多空间使用
例子：引用变治法中的例子，用计数法解决，因为用了对象保存数量。时间复杂度O(n) 空间复杂度O(n)

贪心算法

处理问题，只考虑局部最优，或者从选择最优选项
算法设计过程：处理问题，从最优选项开始
例子：给你一个数组，请你从中抽取一个子序列，满足该子序列的元素之和 严格 大于未包含在该子序列中的各元素之和
示例： [3,4,8,9,2,3] 子序列 [8,9] > [3,4,2,3]
解：我们每次选择最大的元素，判断是否大于剩余的数字的和。

var minSubsequence = function(nums) {
    let sum = nums.reduce((a,b)=>a+b);
    let ret = 0;
    let arr = [];
    nums.sort((a,b)=>b-a)
    for (let i=0; i<nums.length; i++) {
        ret += nums[i];
        sum -= nums[i];
        arr.push(nums[i])
        if (ret > sum) return arr;
    }
};

动态规划

保存计算过的结果，避免重复计算
算法设计过程：

1. 状态转移：保存计算的结果
2. 如果这个条件计算过，则读取计算过的结果

例子： 输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
解：使用蛮力法，组合所有的数字，时间复杂度O(n^2)。这里我们可以使用动态规划

var maxSubArray = function(nums) {
   let max = nums[0];
   for (let i=1; i<nums.length; i++) {
       if (nums[i-1] >= 0) nums[i] = nums[i-1] + nums[i]; // 保存计算过的结果
       max = Math.max(max, nums[i]); // 读取计算过的结果
   }
   return max;
};
// 时间复杂度：O(n)
// 算法分析：我们一个一个往后加，如果前面的和小于0，那么我们就没必要加了

参考资料

《算法设计与分析基础(第3版)》

最后

以上就是糟糕树叶为你收集整理的算法设计方法的全部内容，希望文章能够帮你解决算法设计方法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。