控制算法（一）—— PID控制算法

        比例积分微分控制，简称PID控制，其中P表示比例、I表示积分、D表示微分。PID控制算法是最早发展起来的控制策略之一，由于其算法简单、鲁棒性好和可靠性高，被广泛应用于工业过程控制。而且也衍生出多种相关的控制算法：P控制、PI控制、PD控制、增量式PID控制、模糊PID控制等。虽然这些算法各不相同，但都是基于最基本的PID控制算法为原型的。

        下图为PID控制的示意图

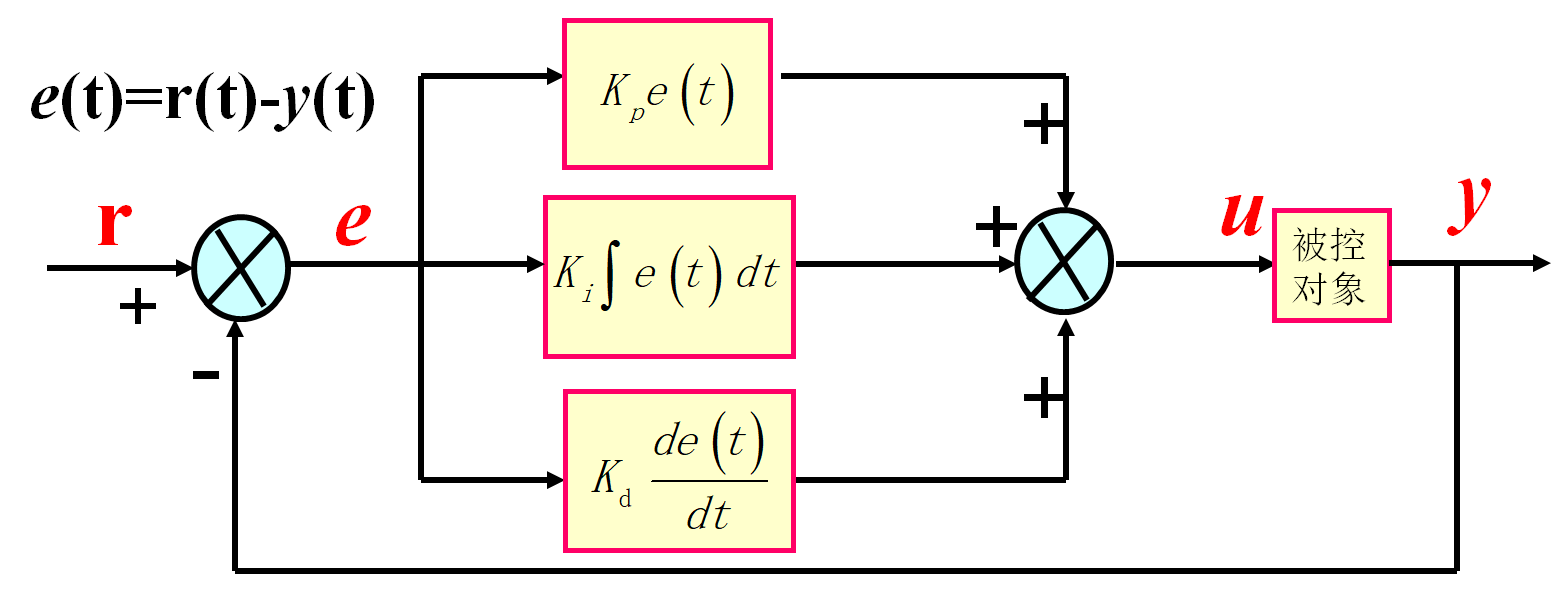
其中r(t)为被控对象状态的期望值，y(t)为被控对象状态的实际值，e(t)为被控对象期望值与实际值之间的偏差，偏差输入给P、I、D三个控制器。、、分别为比例、积分和微分参数，它们是PID控制的基本参数。经过P、I、D三个控制器输出的值加和生成u(t)，u(t)为对被控对象的控制量。u(t)作用在被控对象上导致被控对象的状态y(t)改变。

       下面我们来分析一下P、I、D三个控制的具体作用。

1、P控制

       P控制按偏差e(t)的比例关系对被控对象进行控制，偏差一旦产生，控制器立即产生控制作用，以减小偏差。当仅有比例控制时系统输出存在稳态误差。

       P参数越大，比例作用越强，动态响应越快，消除误差的能力越强。但实际系统是有惯性的，控制输出变化后，实际y(t)值变化还需等待一段时间才会缓慢变化。由于实际系统是有惯性的，比例作用不宜太强，比例作用太强会引起系统振荡不稳定。P参数的大小应在以上定量计算的基础上根据系统响应情况，进行调试决定，通常将P参数由大向小调，以能达到最快响应又无超调为最佳参数。

         P控制比较容易理解，举一个简单的控制，比如一个电控水温加热系统，期望水温为80度。如果当前实际水温小于80度，比如是60度，则偏差e(t)=20，则P控制用20乘以，得到一个正的控制量，这个控制实际上是电控加热的功率附加量。比如我们将水温维持在80度需要的加热功率为X，则在这种情况下，加热的控制量为。如果偏差越大，则加热功率的调节轮越大。如果当前实际水温为90度，则偏差e(t)=-10，则加热的功率控制量为。偏差越大，则对X减小的越多。

2、I控制

       I控制器的输出与输入误差信号的积分成正比关系。I控制主要用于消除静态误差。比例作用的输出与误差的大小成正比，误差越大，输出越大，误差越小，输出越小，误差为零，输出为零。由于没有误差时输出为零，因此比例调节不可能完全消除误差。必定会存在一个稳定的误差，以维持一个稳定的输出。这个控制误差称为静态误差，加强比例作用只能减少静态误差，但不能消除静态误差。

       为了消除静态误差，引入积分控制，积分作用可以消除静差，以使被控对象的状态y(t)值最后与给定值一致。

积分作用消除静态误差的原理是，只要有误差存在，就对误差进行积分，使输出继续增大或减小，一直到误差为零，积分停止，输出不再变化，y(t)值等于u(t)值，达到无差调节的效果。

       但由于实际系统是有惯性的，控制量变化后，y(t)值不会马上变化，须等待一段时间才缓慢变化，因此积分的快慢必须与实际系统的惯性相匹配，惯性大、积分作用就应该弱，积分时间就应该大些。如果积分作用太强，积分输出变化过快，就会引起积分过度的现象，产生积分超调和振荡。

       依然用上面的例子进行说明I控制的作用。如果在调节过程中，水温维持在79度，一直无法达到80度，此时，如果只有P控制，则控制量为。可以看到控制量一直不变，温度也一直上不去，这1度的误差就是静态误差。很显然不加大功率水温是不可能上去的。在这种情况下，我们加入I控制，则控制量变为。加入积分量之后，在原有的控制量基础上加入了积分控制量，而且，稳态误差存在时间越长，积分量越大，控制量也会越大，直到消除稳态误差。

3、D控制

        上面已经分析过，不论比例调节作用，还是积分调节作用都是建立在产生误差后才进行调节以消除误差，都是事后调节，因此这种调节对稳态来说是无差的，对动态来说肯定是有差的，因为对于负载变化或给定值变化所产生的扰动，必须等待产生误差以后，然后再来慢慢调节予以消除。

        但一般的控制系统，不仅对稳定控制有要求，而且对动态指标也有要求，通常都要求负载变化或给定调整等引起扰动后，恢复到稳态的速度要快，因此光有比例和积分调节作用还不能完全满足要求，必须引入微分作用。比例作用和积分作用是事后调节，而微分作用则是事前预防控制，即一发现y(t)有变大或变小的趋势，马上就输出一个阻止其变化的控制信号，以防止出现过冲或超调等。

       D越大，微分作用越强，D越小，微分作用越弱。系统调试时通常把D从小往大调，具体参数由试验决定。

       依然以上面水温的控制为例，如果在加大功率给水加热，水温逐渐上升，每个控制周期增加1度，如果没有D控制，则温度达到80度后，必然会出现超调，然后误差为负后，减小加热功率。如果加入了D控制，则会在上面控制量的基础上加入D环节*，在水温逐渐上升时为负值，则相当于在原有控制量的基础上加了一个负的控制量，从而使总的控制量提前减小，以避免水温的超调。

        由于PID控制应用已经很广泛，前人的经验也有很多可以作为参考，当然也有人总结了很多实用的调试方法。下面奉上几段顺口溜来形象说明PID控制，当然这些顺口溜是在网上抄袭的。

比例作用顺口溜                                                                                              

比例州节器，像个放大器；                                                                

一个偏差来，放大送出去；                                                               

放大是多少，旋钮看仔细；                                                              

比例度旋大，放大倍数低。                                                               

积分作用顺口溜

重定调节器，累积有本领；

只要偏差在，累积不停止； 

累积快与慢，旋钮看仔细；

积分时间长，累积速度低。

微分作用顺口溜 

说起微分器，一点不神秘；

阶跃输入来，输出跳上去；

下降快与慢，旋钮看仔细；

微分时间长，下降就慢些。

下面再奉上一段PID参数调节经验的顺口溜。

参数整定找最佳，从小到大顺序查，

先是比例后积分，最后再把微分加，

曲线振荡很频繁，比例度盘要放大，

曲线漂浮绕大湾，比例度盘往小扳，

曲线偏离回复慢，积分时间往下降，

曲线波动周期长，积分时间再加长，

曲线振荡频率快，先把微分降下来，

动差大来波动慢，微分时间应加长，

理想曲线两个波，前高后低4比1，

一看二调多分析，调节质量不会低。

最后

以上就是伶俐小土豆为你收集整理的控制算法（一）—— PID控制算法的全部内容，希望文章能够帮你解决控制算法（一）—— PID控制算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。