FBI树python题解

题目描述

我们可以把由 0 和 1 组成的字符串分为三类：全 0 串称为 B 串，全 1 串称为 I 串，既含 0 又含 1 的串则称为 F 串。

FBI 树是一种二叉树，它的结点类型也包括 F 结点，B 结点和 I 结点三种。由一个长度为 2^N 的 01 串 S 可以构造出一棵 FBI 树 T，递归的构造方法如下：

1. T 的根结点为 R，其类型与串 S 的类型相同；
2. 若串 S 的长度大于 1，将串 S 从中间分开，分为等长的左右子串 S1​ 和 S2​；由左子串 S1​ 构造 R 的左子树 T1​，由右子串 S2​ 构造 R 的右子树 T2​。

现在给定一个长度为 2^N 的 01 串，请用上述构造方法构造出一棵 FBI 树，并输出它的后序遍历序列。

输入格式

第一行是一个整数 N(0≤N≤10)，

第二行是一个长度为 2^N 的 01 串。

输出格式

一个字符串，即 FBI 树的后序遍历序列。

输入输出样例

输入 #1

3
10001011

输出 #1

IBFBBBFIBFIIIFF

说明/提示

对于 40% 的数据，N≤ 2；

对于全部的数据，N ≤ 10。

noip2004普及组第3题

背景：看到很多人这题选择了先建树再输出，我觉得在空间和时间上都造成了较大的浪费，并且思维上也没有得到较大的提升，所以我打算用python写一篇精炼的题解

首先这题我本人是看了好几次没看懂，所以先给大家画个图理解一下题意

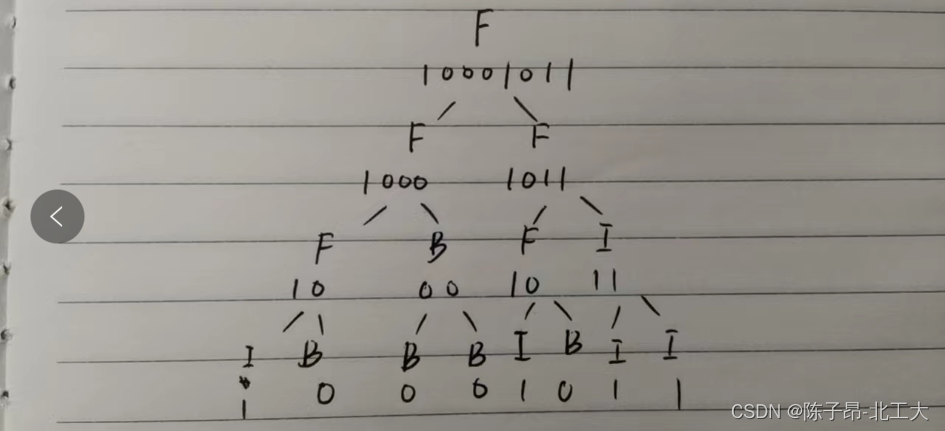
用例要求的就是这棵二叉树的后序遍历 

一般二叉树的题目都是要按左右边界去卡，当左边界等于右边界时输出值并返回。

但是注意这题是一个长度为 2^N 的串，说明了什么？这是个满二叉树！！！最后输出的那层的层数就是n+1，所以到n+1层时，左边界等于右边界，我们直接输出左边界的值就行，省略了右边界的传入和计算，精简了过程

def dfs(step, i, t, n):  # 有步数标记，所以不用右边界了。传入多个因数是为了加快程序的查找速度，不传入t和n程序依然能跑
    if step == n:  # 从0开始，所以到n就行
        print(output := 'B' if t[i] == '0' else 'I', end='')  # 最后一层通过树t判断
    else:
        output1 = dfs(step+1, i, t, n)
        output2 = dfs(step+1, i+2**(n-step-1), t, n)  # 左支的左边界+左支的节点个数=右支的左边界
        print(output := output1 if output1 == output2 else 'F', end='')  # 除了最后一层都通过下一层来判断：下一层的左右支一样就输出左支，下一层的左右支不一样就输出‘F’
    return output  # 返回值都一样，写一个就行


n = int(input())
t = input()
dfs(0, 0, t, n)

最后

以上就是潇洒芝麻为你收集整理的FBI树python题解的全部内容，希望文章能够帮你解决FBI树python题解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。