Viewing transformation 观测变换
view / Cemera transformation 视图变换
Projection transformation 投影变换
Orthographic projection 正交投影
Perspective projection 透视投影
三维变换
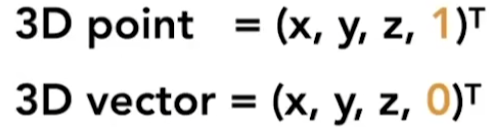
缩放
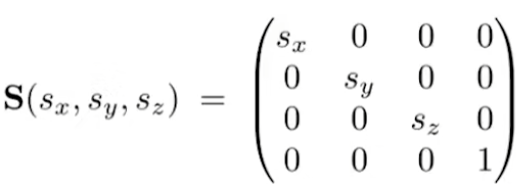
平移
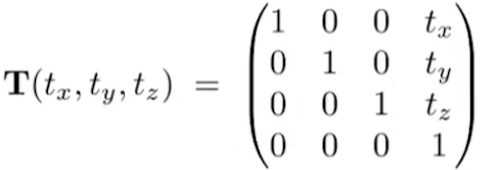
旋转:
如果只绕x旋转:
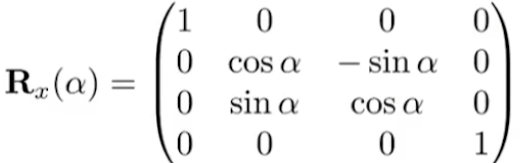
只绕y旋转:
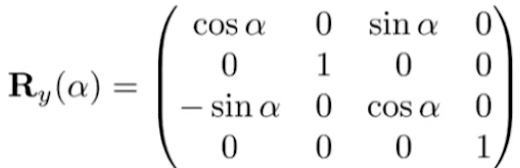
只绕z旋转:
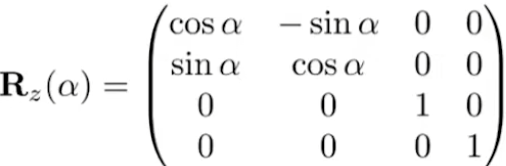
发现和二维很像
那三维中的旋转分解成对xyz轴的旋转
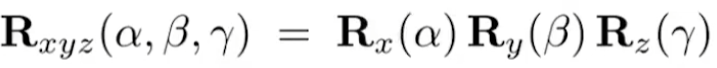
这三个角被称为欧拉角
图形学里就有人用任意一个旋转写成矩阵方法就是分解成xyz分别做旋转的出来的
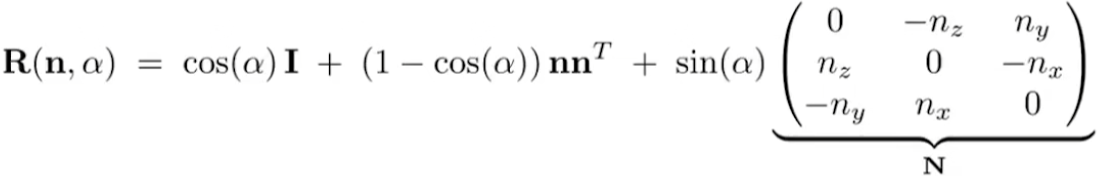
就叫罗德里格斯旋转公式
从三维变成一张图(二维)
什么是视图变换
模型变换
视图变换(改变相机)
模型和视图做一个投影
简称MVP变换 (model view projection)
相机的位置非常重要,首先要定义它 Position
然后就是相机看的方向 look at direction
最后就是相机的向上方向Up direction (看的方向是可以旋转)
因为相对静止的时候,拍照的结果都是一样的所以。
约定:相机永远在原点,永远向-Z方向看,相机永远以Y轴为向上方向
怎么移动到这个位置?
首先把位置移动到原点
把方向旋转到-Z
把向上方向旋转到Y
透视投影会发现平行线不再平行,会相交在某个地方(类似人眼)
正交投影更多用来做工程制图(正交投影并不会给人带来一种进大远小的现象)
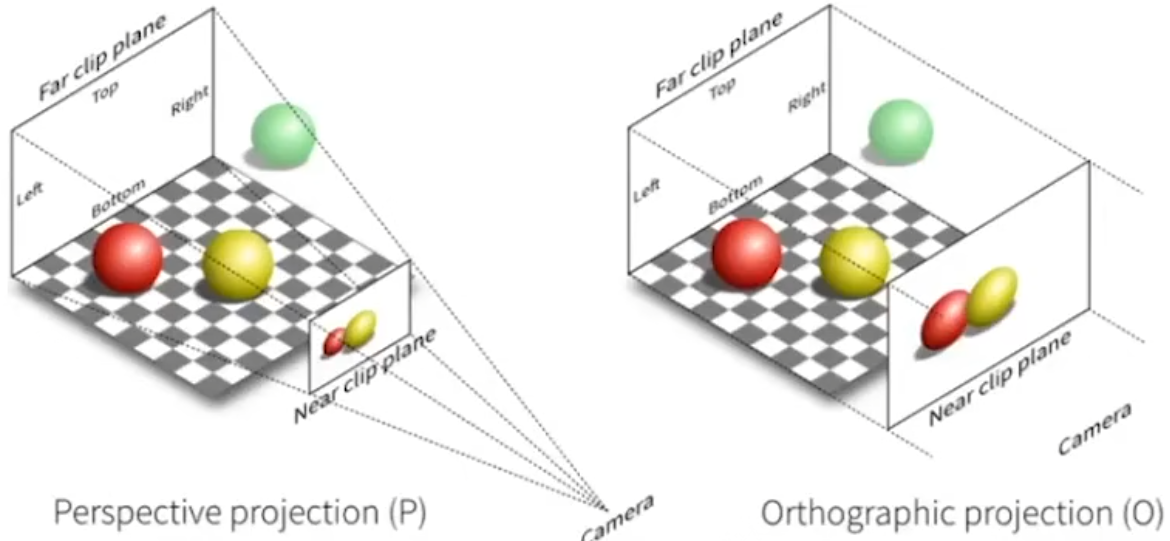
正交投影:
把相机放在原点,朝-Z看,向上是Y
把Z坐标扔掉(就都是XY了)
但正式的方法不是这样做。
定义一个空间中的立方体
中心平移到原点 缩放成标准立方体[-1,1]3
在x轴上定义左和右[l, r] y轴定义 下和上 [b, t] z轴定义远和近 [f, n] (因为向-Z看 f < n)
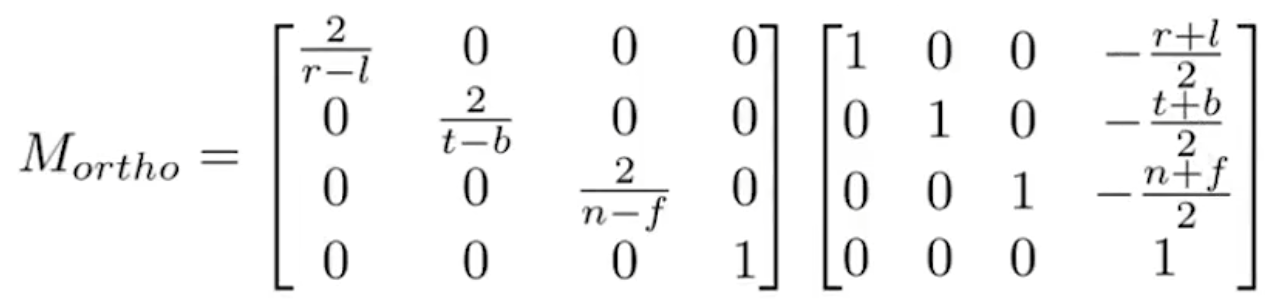
透视投影:
齐次坐标系中点 (x,y,z,1)=> (kx, ky, kz, k) => (xz, yz, zz, z) z != 0
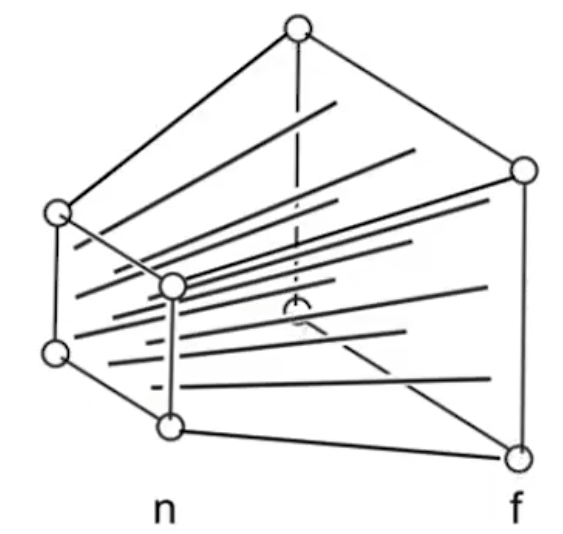
可以拿到远平面四个点挤到和近平面同一高度,然后通过正交投影就可以
规定:
近平面永远不变
Z轴不变
中心点不会变
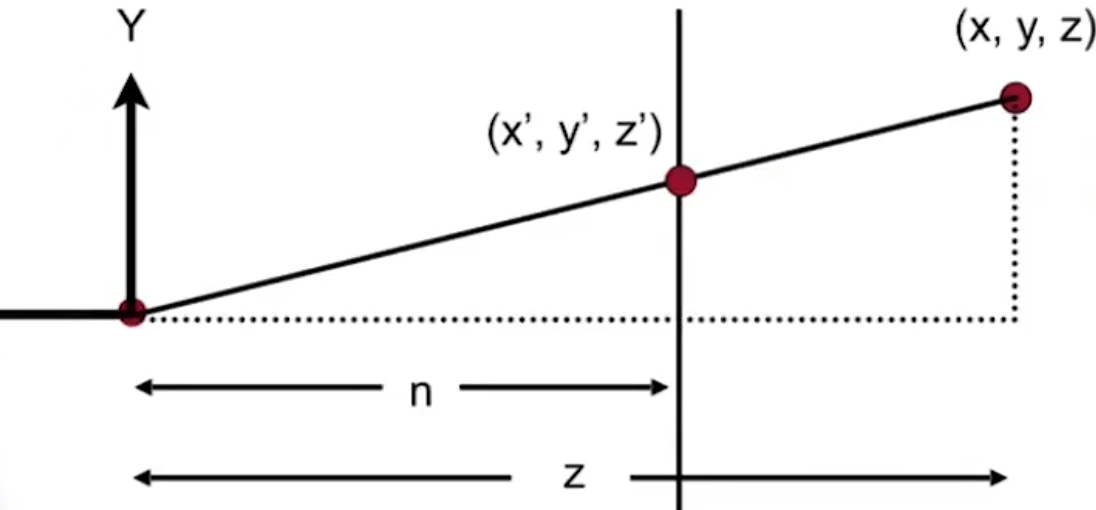
会发现这里有一对相似三角形
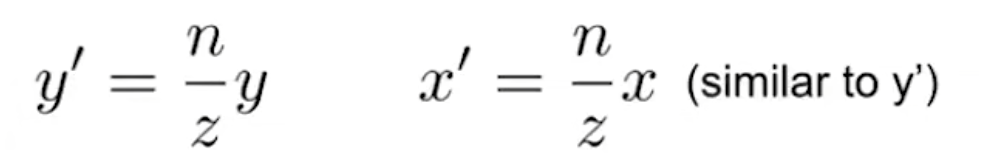
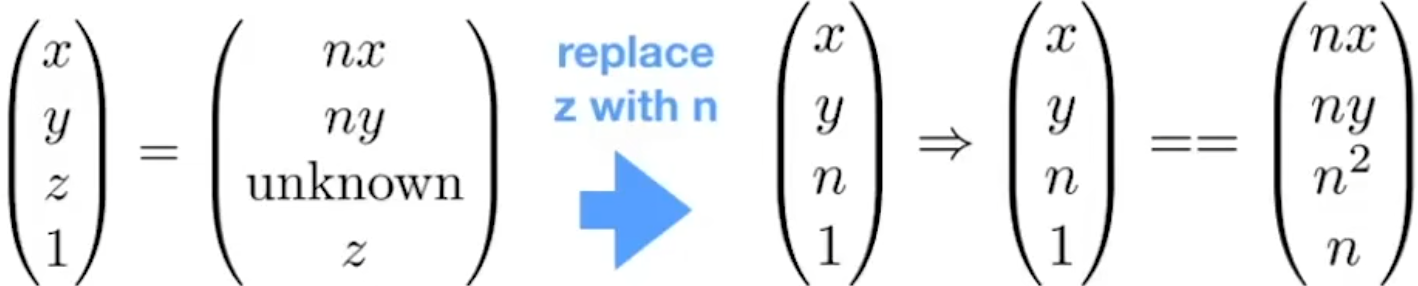
(0,0,f,1)=>(0,0,f,1) => (0,0,ff,f)
(0,0,A,B)(x,y,n,1) =nn

投影矩阵
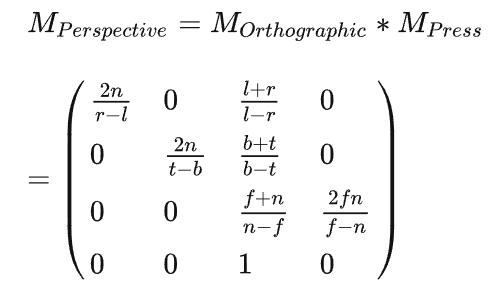
最后
以上就是落寞长颈鹿最近收集整理的关于图形 (变换2)的全部内容,更多相关图形内容请搜索靠谱客的其他文章。








发表评论 取消回复