概述
Decision Tree 决策树
- 决策树案例
- Entropy熵
- Entropy Notation 熵公式
- 熵图像
- Information Gain 信息增益
- 采用最大信息增益方法建立决策树如下：
- QA
- QA1：若有特征不仅仅有两个特征值，假设有三个怎么办
- QA2：若特征值为连续值而非离散值该怎么办
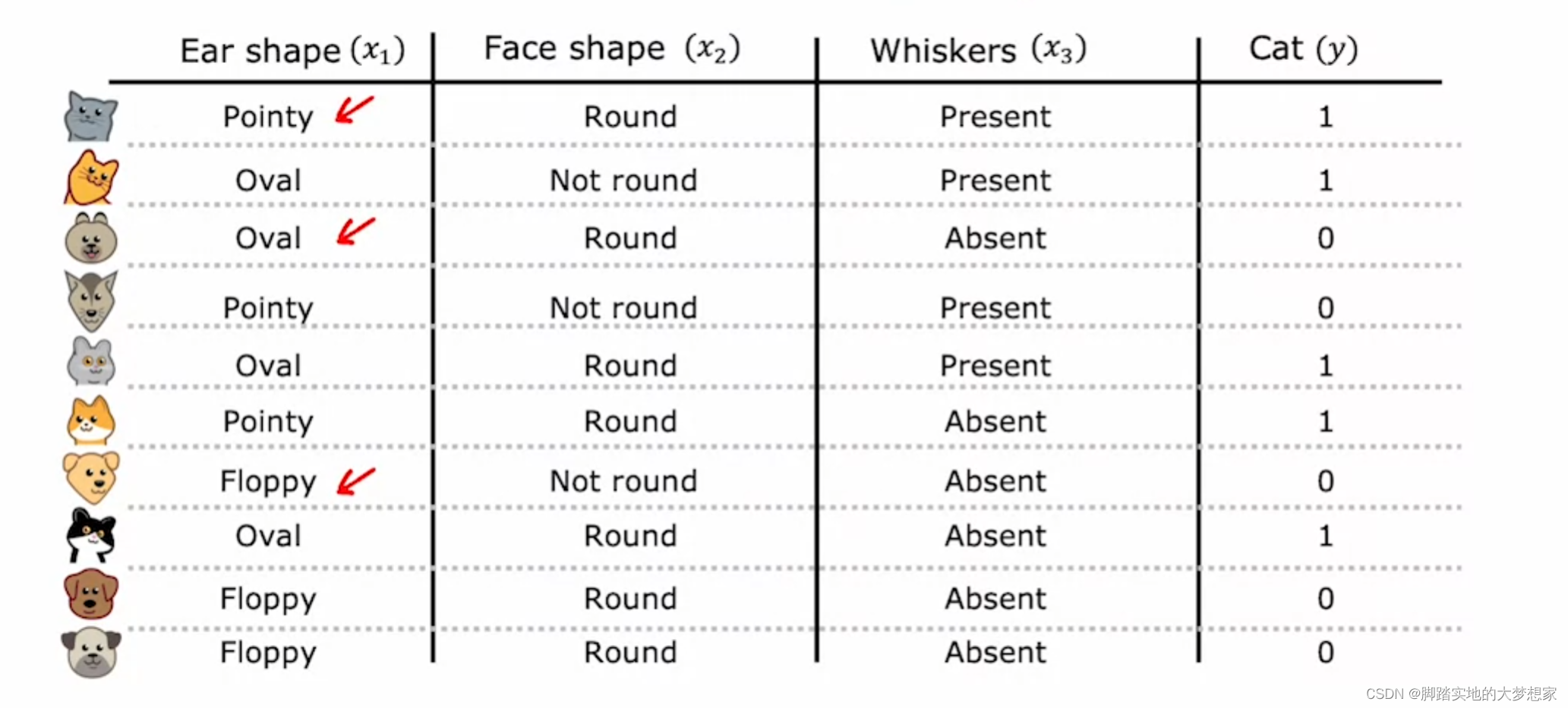
决策树案例
数据来源：吴恩达《Machine Learning》Decision Tree Model-Cat Recognizer
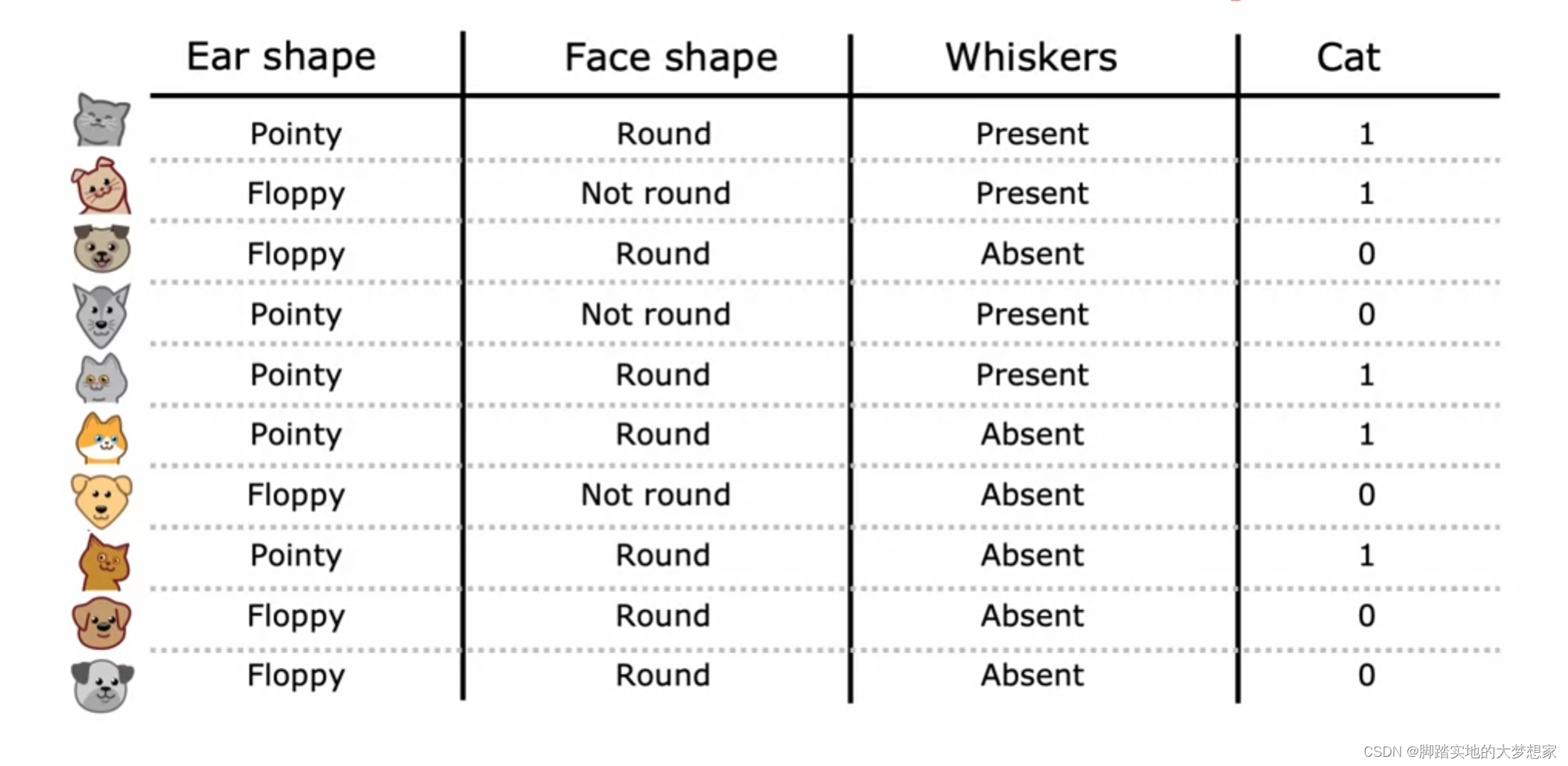
上表中包含三个特征以及最后一列是否为猫的结果，所以可以根据三个 特征(features) 构建决策树如下：
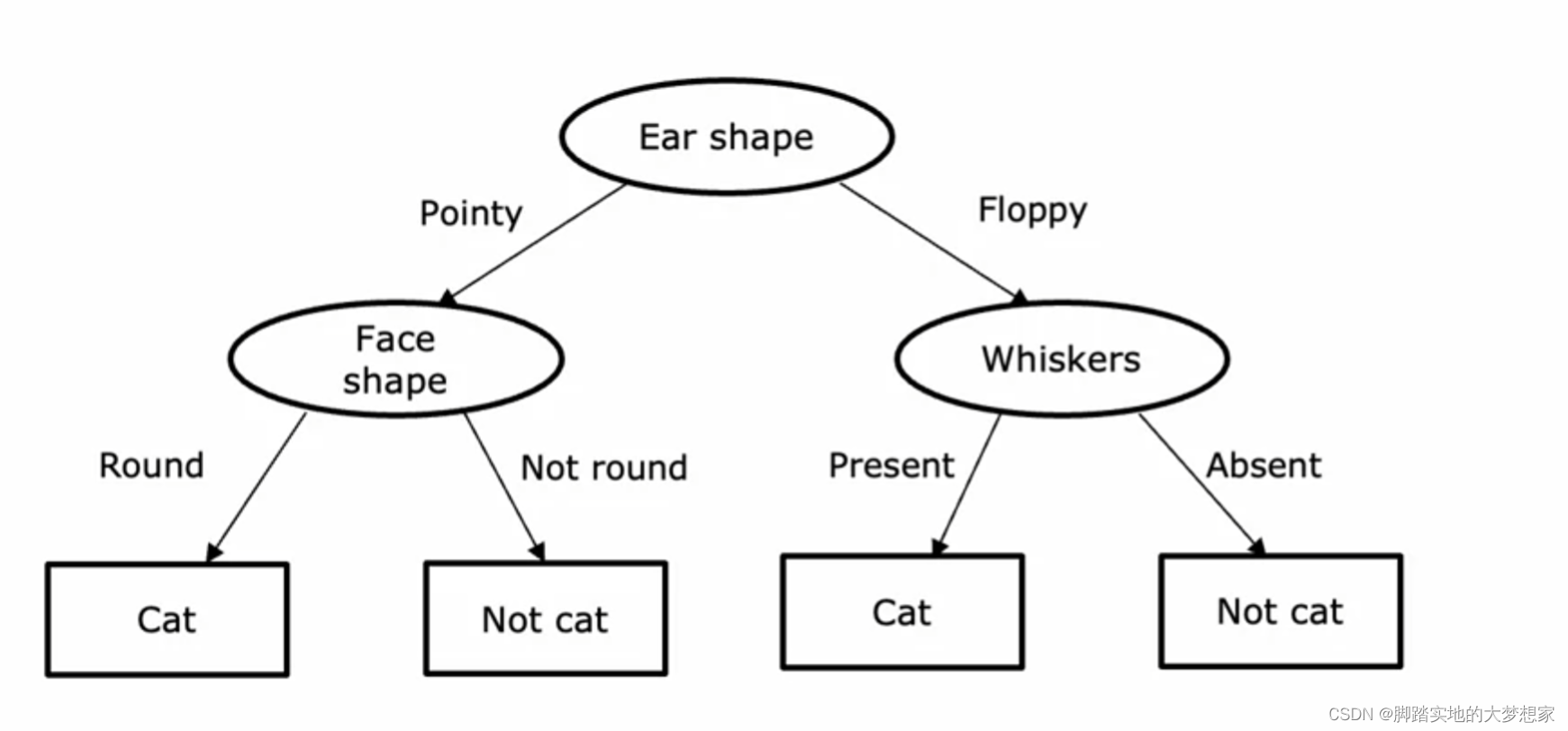
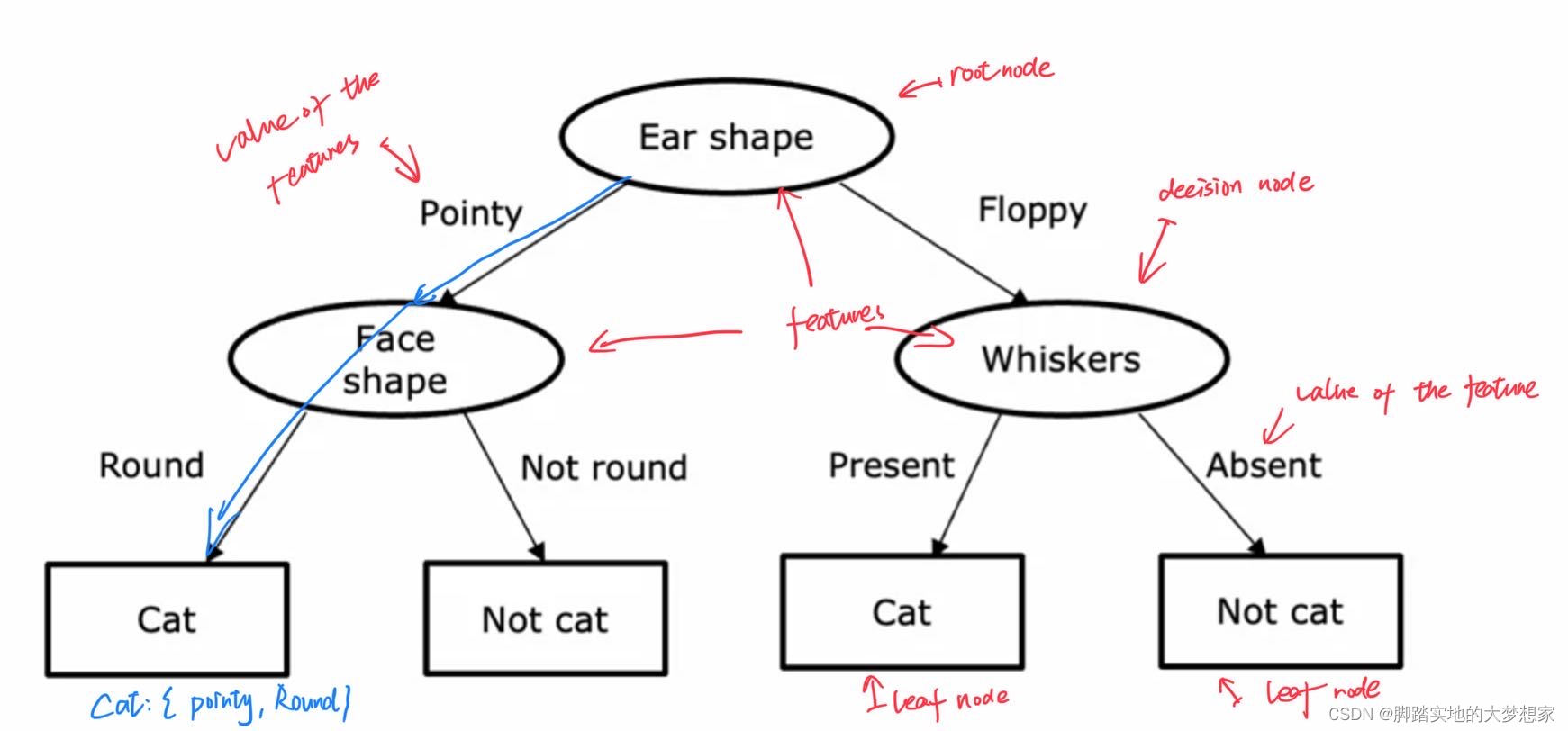
一般来说，一个决策树包含一个 根节点(Root Node)，很多 决定结点(decision nodes) 以及 叶子结点(leaf nodes)。
决策树从根节点出发，根据对特征值的分类，走向不同的分支。不同的分支再根据决策结点、按照特征值的方式进行分类，以此往复，从而最终抵达叶子结点。
Entropy熵
通过上述构建简单的决策树介绍了决策树的基本概念：根节点、决策节点、叶子节点、特征与特征值等概念。
下面将介绍 熵(Entropy) 的概念、计算方法与函数图像。
Entropy Notation 熵公式
熵描述的是事件的不确定性。
假设事件只有两种可能结果，那么概率以及熵的计算公式如下：
p
0
=
1
−
p
1
p_0 = 1-p_1
p0=1−p1
H
(
p
1
)
=
−
p
1
l
o
g
2
(
p
1
)
−
p
0
l
o
g
2
(
p
0
)
H(p_1)=-p_1log_2(p_1)-p_0log_2(p_0)
H(p1)=−p1log2(p1)−p0log2(p0)
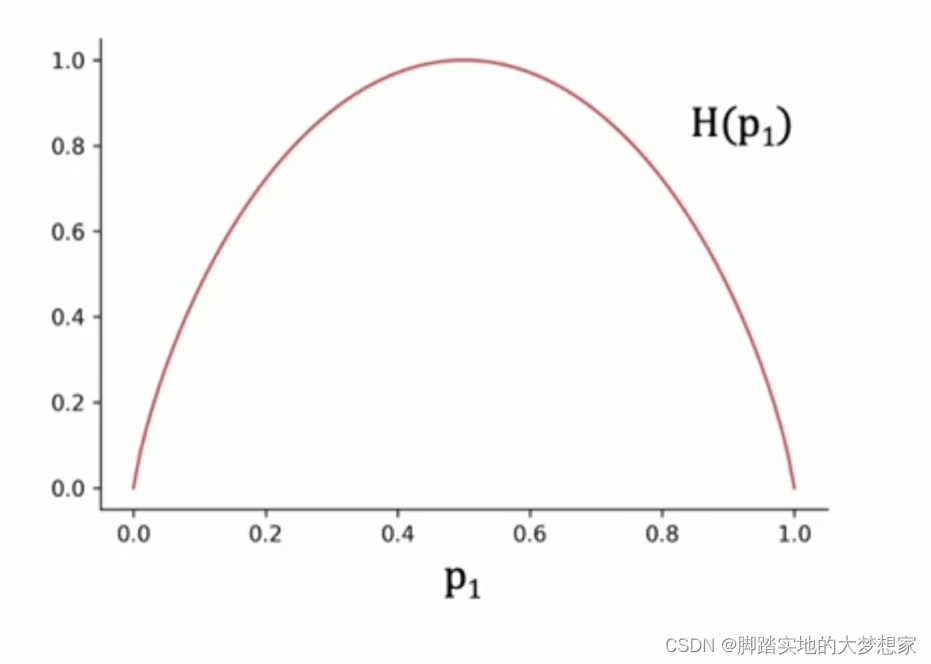
熵图像
若
P
1
P_1
P1 为
0.2
0.2
0.2 时，
H
(
0.2
)
=
−
0.2
l
o
g
2
(
0.2
)
−
(
1
−
0.2
)
l
o
g
2
(
1
−
0.2
)
H(0.2)=-0.2log_2(0.2)-(1-0.2)log_2(1-0.2)
H(0.2)=−0.2log2(0.2)−(1−0.2)log2(1−0.2)
若
P
1
P_1
P1 为
0.8
0.8
0.8 时，
H
(
0.8
)
=
−
0.8
l
o
g
2
(
0.8
)
−
(
1
−
0.8
)
l
o
g
2
(
1
−
0.8
)
=
H
(
0.2
)
H(0.8)=-0.8log_2(0.8)-(1-0.8)log_2(1-0.8)=H(0.2)
H(0.8)=−0.8log2(0.8)−(1−0.8)log2(1−0.8)=H(0.2)
即熵函数关于 P = 0.5 P=0.5 P=0.5 对称。
Information Gain 信息增益
说回决策树，信息增益是判断决策树的每个决定节点如何安排的决定因素。
有点绕，拿案例来举例：
e
.
g
.
e.g.
e.g. 案例如图所示。
采用最大信息增益方法建立决策树如下：
首先计算每个特征下特征值的概率，然后根据概率求得熵的值。根据熵的值计算信息增益
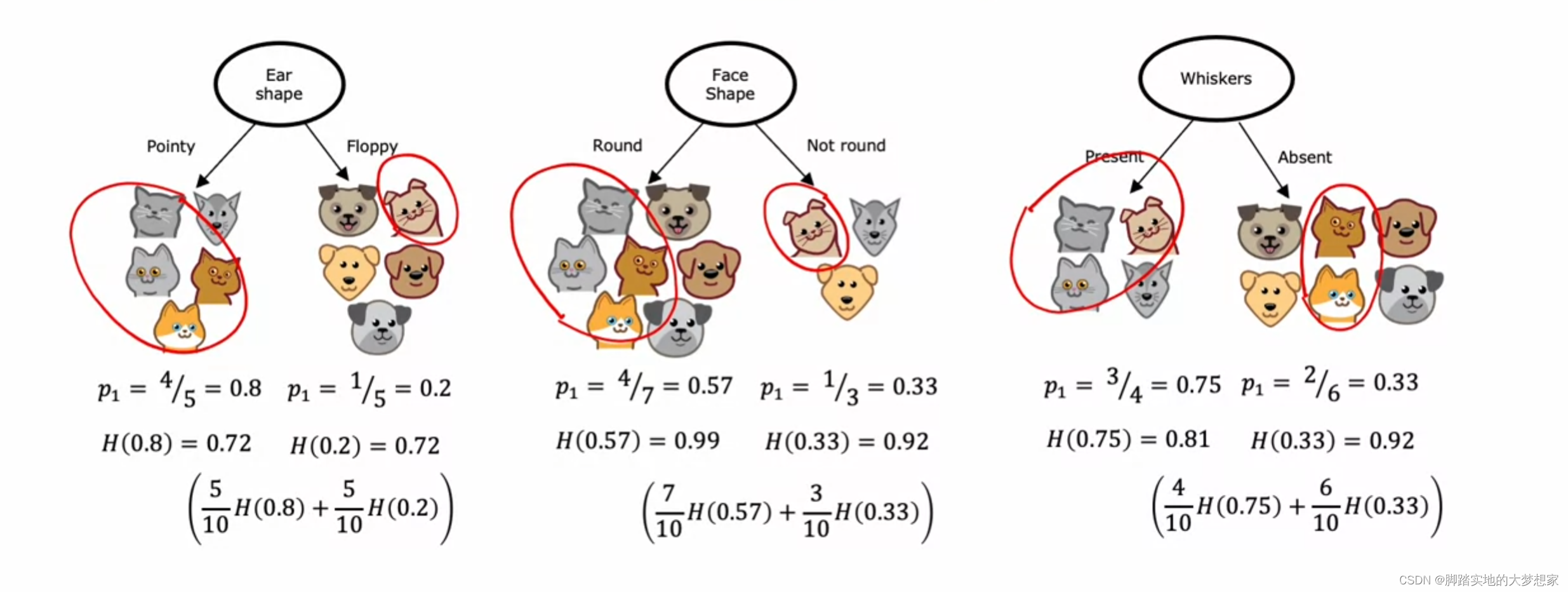
若采用 Ear shape 作为根节点，其信息增益为：
H
(
0.5
)
−
(
5
10
H
(
0.8
)
+
5
10
H
(
0.2
)
)
H(0.5) - (frac 5 {10} H(0.8)+ frac 5 {10} H(0.2))
H(0.5)−(105H(0.8)+105H(0.2))
若采用 Face shape 作为根节点，其信息增益为：
H
(
0.5
)
−
(
7
10
H
(
0.57
)
+
3
10
H
(
0.33
)
)
H(0.5) - (frac 7 {10} H(0.57)+ frac 3 {10} H(0.33))
H(0.5)−(107H(0.57)+103H(0.33))
若采用 Whiskers 作为根节点，其信息增益为：
H
(
0.5
)
−
(
4
10
H
(
0.75
)
+
6
10
H
(
0.33
)
)
H(0.5) - (frac 4 {10} H(0.75)+ frac 6 {10} H(0.33))
H(0.5)−(104H(0.75)+106H(0.33))
其中最大信息增益为 Ear Shape。所以将该特征作为根节点，根据特征值将其分为两类， Pointy 以及 Floppy。
然后将分好两类的决策树再计算其概率以及熵，然后再根据其最大信息增益安排下一个要判断的特征。
QA
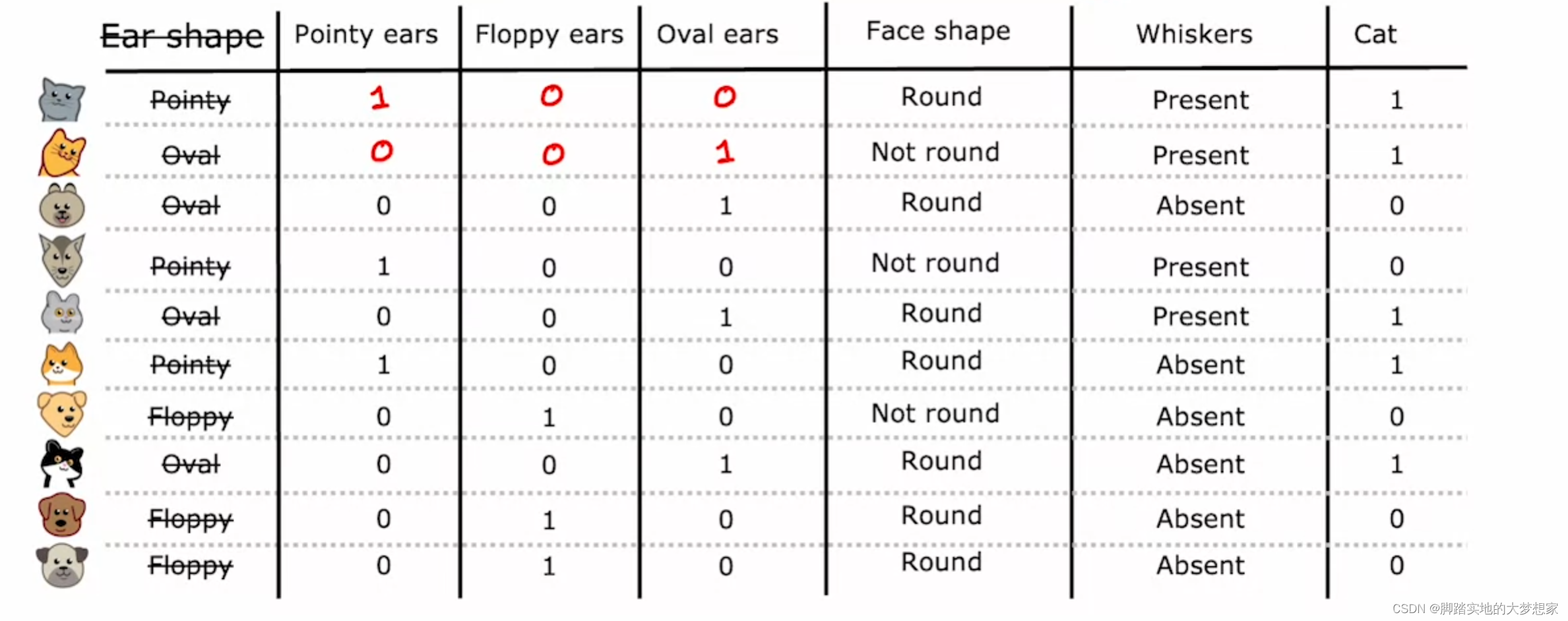
QA1：若有特征不仅仅有两个特征值，假设有三个怎么办
下图中 Ear Shape 特征包含三个特征值。处理方案为将三个特征值分别化为三个特征对待，方法如下图所示：
图片来源：吴恩达《Machine Learning》仅用于学习参考
将包含三个特征值的 Ear Shape 特征划分为三个特征来对待：
QA2：若特征值为连续值而非离散值该怎么办
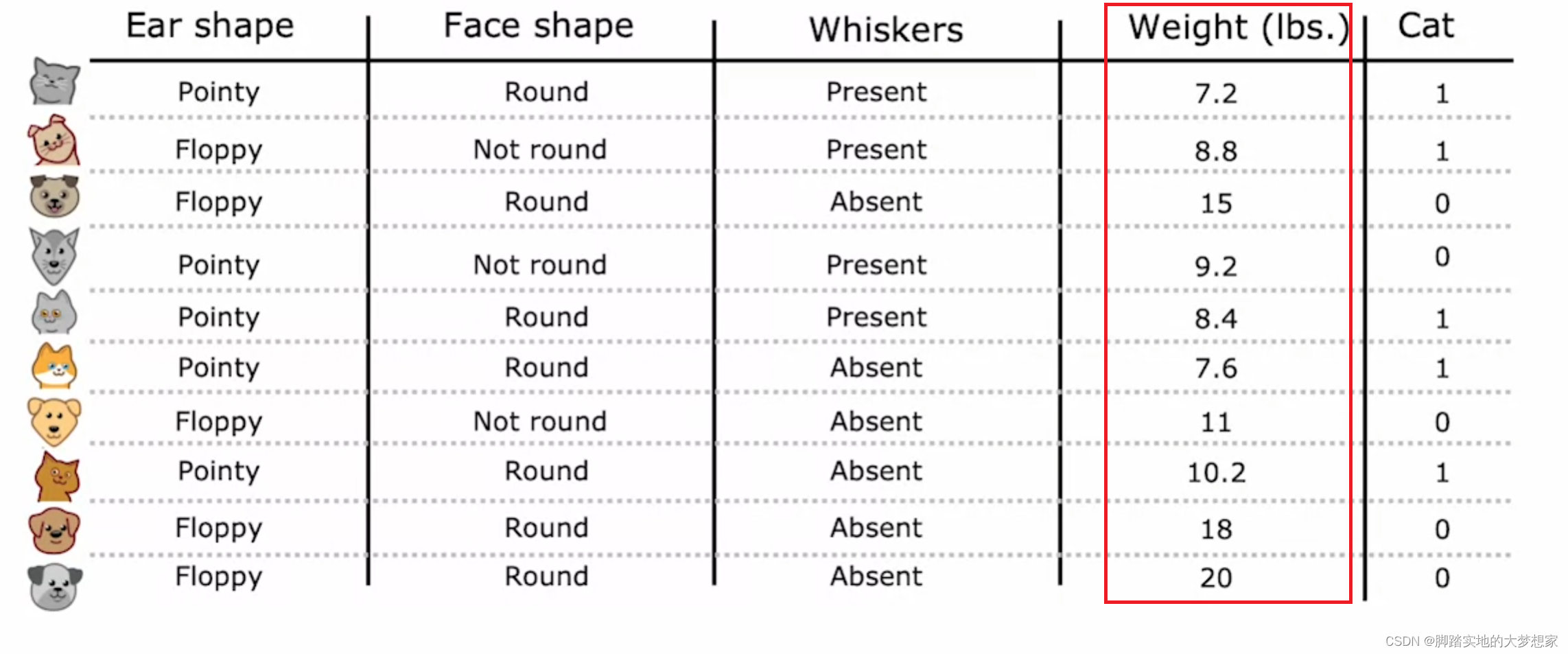
上图中，Weight 属性为连续值而非离散值，处理方案为我们可以将其按照 Weight>10 以及 Weight≤10 分成两类来处理。
最后
以上就是怕孤独水池为你收集整理的【ML25】Decision Tree 决策树概念决策树案例Entropy熵Information Gain 信息增益QA的全部内容，希望文章能够帮你解决【ML25】Decision Tree 决策树概念决策树案例Entropy熵Information Gain 信息增益QA所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复