决策树分类(decision tree classification)和python实现特征选择连续值处理剪枝处理

74 阅读 0 评论 49 点赞

我是靠谱客的博主舒心河马，最近开发中收集的这篇文章主要介绍决策树分类(decision tree classification)和python实现特征选择连续值处理剪枝处理，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

决策树分类很符合人类分类时的思想，决策树分类时会提出很多不同的问题，判断样本的某个特征，然后综合所有的判断结果给出样本的类别。例如下图的流程即为一个典型的决策树分类的流程图，这个流程图用来简略的判断一个小学生是否学习很好，当然这里只是举个例子，现在的小学生可是厉害的不行了，这点评判标准完全不够看啊。。。

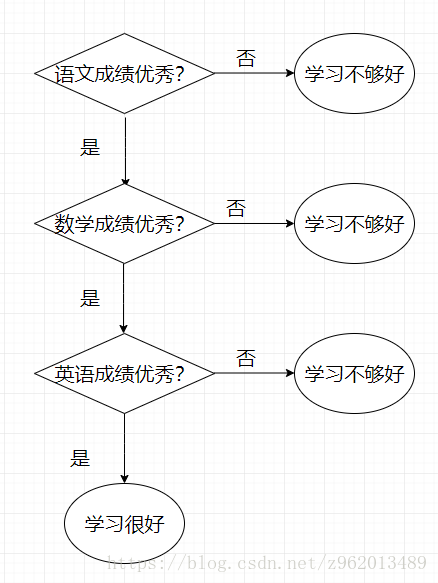
这里写图片描述
说白了决策树就是if else的堆砌，是一个树形结构，我们在构建决策树分类器的时候主要关心的是用什么特征分类和分多少个枝叶。

特征选择

首先我们来说说特征选择，我们给出如下表所示的一系列样本

样本	花瓣颜色	花蕊长度	树叶类型	种类
1	绿色	高	三角	A
2	红色	高	方形	B
3	绿色	低	三角	B
4	绿色	高	方形	A
5	红色	低	三角	B
6	绿色	低	方形	B

我们要根据花瓣颜色、花蕊长度和树叶类型这三个特征对样本植物辨别出其种类A或B，那么应该以什么样的标准选择特征呢？

信息增益

“信息熵”(information entropy)是度量样本集合纯度的一种常用指标，若集合D中存在d个类别的N个样本，令 $p_{k}=frac{N_{k}}{N}$ 为从集合D中随机选取一个样本属于第k类样本的概率，则有下述信息熵定义：
$Ent(D)=-sum_{k=1}^{d}p_{k}log_{2}p_{k}$
我们可以计算一下上表样本集的信息熵：
$Ent(D)=-frac{2}{6}*log_{2}frac{2}{6}--frac{4}{6}*log_{2}frac{4}{6}=0.9183$
假如某离散属性a有V个可能的取值，如属性花瓣颜色方面有2个可能的取值：绿色、红色。若选取属性a对样本集D划分，则会产生V个分支，第v个分支上的样本数量为 $N_{v}$ ，我们可以计算出各分支的信息熵，根据各分支拥有的样本与总样本数的比值作为各分支节点的权重，于是有下述信息增益(information gain)定义：
$Gain(D,a)=Ent(D)-sum_{v=1}^{V}frac{N_{v}}{N}Ent(D_{v})$
上面的话不好理解，我们带入一个例子就轻松多了：选取属性为a=花瓣颜色，那么V=2(绿色、红色)，样本集D含有N=6个样本，经过花瓣颜色的分类后出现了 $D_{1}$ 、 $D_{2}$ 两个样本集，其中 $D_{1}$ 中含有的样本数 $N_{1}=4$ ， $D_{2}$ 中含有的样本数 $N_{2}=2$ ，那么：
$Ent(D_{1})=-frac{2}{4}*log_{2}frac{2}{4}-frac{2}{4}*log_{2}frac{2}{4}=1$
$Ent(D_{2})=-frac{2}{2}*log_{2}frac{2}{2}=0$
$color)=Ent(D)-frac{4}{6}Ent(D_{1})-frac{2}{6}Ent(D_{2})=0.2516$
通常信息增益越大，则意味着使用属性a划分所获得的样本集合的综合纯度越大，著名的ID3决策树学习算法就是以信息增益为准则选取属性划分决策树的。
我们这里继续计算另外两个属性的Gain：
$G a i n (D, P i s t i l L e n g t h) = 0.4592$
$G a i n (D, L e a f T y p e) = 0$
经过比较后我们发现属性花蕊长度是最优的属性，那么我们选择花蕊长度划分作为我们决策树的根节点
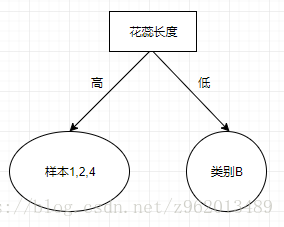
这里写图片描述
经过划分后我们发现凡是花蕊长度低的花都是B类，那么我们就将右边的节点设为叶子节点，然后我们继续分析左边的节点应该选择什么属性继续划分,这里我们直接不考虑属性花蕊长度，我们将样本1，2，4构成的样本集称为DD，则：
$Ent(DD)=-frac{2}{3}*log_{2}frac{2}{3}--frac{1}{3}*log_{2}frac{1}{3}=0.9183$
$G a i n (D D, P e t a l C o l o r) = 0.9183$
$G a i n (D D, L e a f T y p e) = 0.4183$
因此选择花瓣颜色作为进一步划分的属性，经过这一步后我们已经将所有节点都分完了类，获得了下图的决策树：
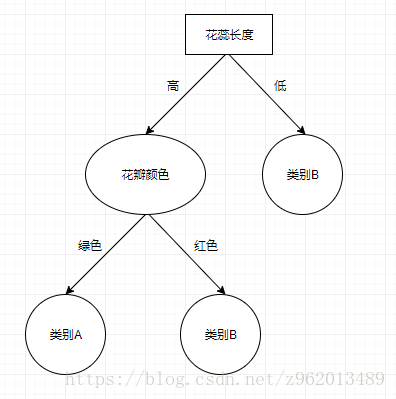
这里写图片描述

增益率

在上表中，如果我们再添加一个属性为样本编号，那么计算得到的信息增益 $G a i n (D, L a b e l) = 0.9183$ 是最大的，但是我们可以明显发现这样分类并不是最优的，这样的节点不具有泛化能力，于是提出了增益率(gain ratio)的概念，C4.5决策树算法就是采用这种方法选择最优属性的：
$G a i n R a t i o ( D , a ) = G a i n ( D , a ) I V ( a ) GainRatio(D,a)=frac{Gain(D,a)}{IV(a)}$
$IV(a)=-sum_{v=1}^{V}frac{N_{v}}{N}log_{2}frac{N_{v}}{N}$
我们会选择增益率最高的属性作为我们的最优的划分属性， $I V (a)$ 为属性a的“固有值”，实际上就是样本集D通过属性a来分类的信息熵，属性a的取值越多，固有值越大，因此可以使用增益率防止选择了上述情况的错误属性。但是这里值得注意的是增益率可能会对取值数目较少的属性有偏好，因此C4.5算法首先计算各属性的信息增益，其中超过平均值的属性才进一步计算增益率来选择最优属性。

基尼指数

基尼值是指从一个样本集中选择2个样本，这2个样本不属于同一类的概率：
$Gini(D)=1-sum_{v=1}^{d}p_{v}^{2}$
可以看出基尼值越小说明该数据集中不同类的数据越少，即数据集纯度越高
将基尼值应用到选择特征方面，我们可以计算通过属性a划分后各样本集的基尼值和权重的积的和来衡量选择属性的判据：
$GiniIndex(D,a)=sum_{v=1}^{V}frac{N_{v}}{N}Gini(D_{v})$
我们选择基尼指数最小的属性作为我们的最优的划分属性，这样得到的决策树叫CART决策树

我们这里总结一下：

信息增益：根据信息熵选择可以带来最大信息增益的属性，缺点是可能对含有较多取值的属性有偏好
增益率：对信息增益加了一个分母，移除了信息增益对含有较多取值的属性有偏好，但是随之而来的是对含有较少取值的属性的偏好，通常使用时首先选择信息增益超过平均值的属性，再从这些属性中选择增益率最大的属性
基尼指数：根据从样本集中选择2个样本其类别不一样的概率选择最优划分属性，基尼指数越小越好
上面我们一直说的属性都是离散值，对于离散值的属性，一旦使用过就不能再使用，而连续值则可以多次使用

连续值处理

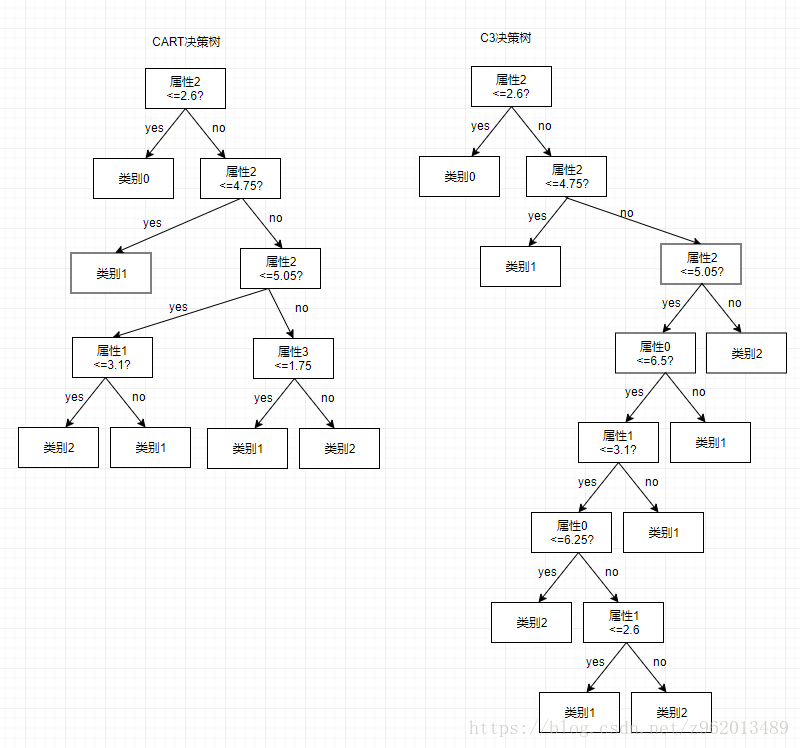
我们这里使用iris数据集进行决策树分类，该数据集中一共有3个类，4个属性，这4个属性都是连续值，最简单的方法是采用二分法对连续属性进行处理，对一个连续属性a“叶子长度”，我们对样本集中的所有属性a的取值（比如有3.9, 5.2, 2.3, 4.4）升序排序(2.3, 3.9, 4.4, 5.2)，然后取属性a相邻两个取值的平均值（3.1, 4.15, 4.8）作为阈值进行二分类，然后计算不同阈值下的信息增益/基尼指数，选择属性a下的最佳阈值。按照这种方法将所有属性都计算其最佳信息增益/基尼指数来选择最佳属性。

以下是我们从iris数据集中随机选择100个样本作为训练集，50个样本作为测试集，分别使用信息增益和基尼指数作为选择属性的方法获得的决策树，使用测试集测试后，CARTA决策树分类正确49个，C3决策树分类正确47个。
这里写图片描述

python实现

python3.6实现ID3决策树和CART决策树如下：

from sklearn.datasets import load_iris
import numpy as np
import math
from collections import Counter


class decisionnode:
    def __init__(self, d=None, thre=None, results=None, NH=None, lb=None, rb=None, max_label=None):
        self.d = d   # d表示维度
        self.thre = thre  # thre表示二分时的比较值，将样本集分为2类
        self.results = results  # 最后的叶节点代表的类别
        self.NH = NH  # 存储各节点的样本量与经验熵的乘积，便于剪枝时使用
        self.lb = lb  # desision node,对应于样本在d维的数据小于thre时，树上相对于当前节点的子树上的节点
        self.rb = rb  # desision node,对应于样本在d维的数据大于thre时，树上相对于当前节点的子树上的节点
        self.max_label = max_label  # 记录当前节点包含的label中同类最多的label


def entropy(y):
    '''
    计算信息熵，y为labels
    '''

    if y.size > 1:

        category = list(set(y))
    else:

        category = [y.item()]
        y = [y.item()]

    ent = 0

    for label in category:
        p = len([label_ for label_ in y if label_ == label]) / len(y)
        ent += -p * math.log(p, 2)

    return ent


def Gini(y):
    '''
    计算基尼指数，y为labels
    '''
    category = list(set(y))
    gini = 1

    for label in category:
        p = len([label_ for label_ in y if label_ == label]) / len(y)
        gini += -p * p

    return gini


def GainEnt_max(X, y, d):
    '''
    计算选择属性attr的最大信息增益，X为样本集,y为label，d为一个维度，type为int
    '''
    ent_X = entropy(y)
    X_attr = X[:, d]
    X_attr = list(set(X_attr))
    X_attr = sorted(X_attr)
    Gain = 0
    thre = 0

    for i in range(len(X_attr) - 1):
        thre_temp = (X_attr[i] + X_attr[i + 1]) / 2
        y_small_index = [i_arg for i_arg in range(
            len(X[:, d])) if X[i_arg, d] <= thre_temp]
        y_big_index = [i_arg for i_arg in range(
            len(X[:, d])) if X[i_arg, d] > thre_temp]
        y_small = y[y_small_index]
        y_big = y[y_big_index]

        Gain_temp = ent_X - (len(y_small) / len(y)) * 
            entropy(y_small) - (len(y_big) / len(y)) * entropy(y_big)
        '''
        intrinsic_value = -(len(y_small) / len(y)) * math.log(len(y_small) /
                                                              len(y), 2) - (len(y_big) / len(y)) * math.log(len(y_big) / len(y), 2)
        Gain_temp = Gain_temp / intrinsic_value
        '''
        # print(Gain_temp)
        if Gain < Gain_temp:
            Gain = Gain_temp
            thre = thre_temp
    return Gain, thre


def Gini_index_min(X, y, d):
    '''
    计算选择属性attr的最小基尼指数，X为样本集,y为label，d为一个维度，type为int
    '''

    X = X.reshape(-1, len(X.T))
    X_attr = X[:, d]
    X_attr = list(set(X_attr))
    X_attr = sorted(X_attr)
    Gini_index = 1
    thre = 0

    for i in range(len(X_attr) - 1):
        thre_temp = (X_attr[i] + X_attr[i + 1]) / 2
        y_small_index = [i_arg for i_arg in range(
            len(X[:, d])) if X[i_arg, d] <= thre_temp]

        y_big_index = [i_arg for i_arg in range(
            len(X[:, d])) if X[i_arg, d] > thre_temp]
        y_small = y[y_small_index]
        y_big = y[y_big_index]

        Gini_index_temp = (len(y_small) / len(y)) * 
            Gini(y_small) + (len(y_big) / len(y)) * Gini(y_big)
        if Gini_index > Gini_index_temp:
            Gini_index = Gini_index_temp
            thre = thre_temp
    return Gini_index, thre


def attribute_based_on_GainEnt(X, y):
    '''
    基于信息增益选择最优属性，X为样本集，y为label
    '''
    D = np.arange(len(X[0]))
    Gain_max = 0
    thre_ = 0
    d_ = 0
    for d in D:
        Gain, thre = GainEnt_max(X, y, d)
        if Gain_max < Gain:
            Gain_max = Gain
            thre_ = thre
            d_ = d  # 维度标号

    return Gain_max, thre_, d_


def attribute_based_on_Giniindex(X, y):
    '''
    基于信息增益选择最优属性，X为样本集，y为label
    '''
    D = np.arange(len(X.T))
    Gini_Index_Min = 1
    thre_ = 0
    d_ = 0
    for d in D:
        Gini_index, thre = Gini_index_min(X, y, d)
        if Gini_Index_Min > Gini_index:
            Gini_Index_Min = Gini_index
            thre_ = thre
            d_ = d  # 维度标号

    return Gini_Index_Min, thre_, d_


def devide_group(X, y, thre, d):
    '''
    按照维度d下阈值为thre分为两类并返回
    '''
    X_in_d = X[:, d]
    x_small_index = [i_arg for i_arg in range(
        len(X[:, d])) if X[i_arg, d] <= thre]
    x_big_index = [i_arg for i_arg in range(
        len(X[:, d])) if X[i_arg, d] > thre]

    X_small = X[x_small_index]
    y_small = y[x_small_index]
    X_big = X[x_big_index]
    y_big = y[x_big_index]
    return X_small, y_small, X_big, y_big


def NtHt(y):
    '''
    计算经验熵与样本数的乘积，用来剪枝，y为labels
    '''
    ent = entropy(y)
    print('ent={},y_len={},all={}'.format(ent, len(y), ent * len(y)))
    return ent * len(y)


def maxlabel(y):
    label_ = Counter(y).most_common(1)
    return label_[0][0]


def buildtree(X, y, method='Gini'):
    '''
    递归的方式构建决策树
    '''
    if y.size > 1:
        if method == 'Gini':
            Gain_max, thre, d = attribute_based_on_Giniindex(X, y)
        elif method == 'GainEnt':
            Gain_max, thre, d = attribute_based_on_GainEnt(X, y)
        if (Gain_max > 0 and method == 'GainEnt') or (Gain_max >= 0 and len(list(set(y))) > 1 and method == 'Gini'):
            X_small, y_small, X_big, y_big = devide_group(X, y, thre, d)
            left_branch = buildtree(X_small, y_small, method=method)
            right_branch = buildtree(X_big, y_big, method=method)
            nh = NtHt(y)
            max_label = maxlabel(y)
            return decisionnode(d=d, thre=thre, NH=nh, lb=left_branch, rb=right_branch, max_label=max_label)
        else:
            nh = NtHt(y)
            max_label = maxlabel(y)
            return decisionnode(results=y[0], NH=nh, max_label=max_label)
    else:
        nh = NtHt(y)
        max_label = maxlabel(y)
        return decisionnode(results=y.item(), NH=nh, max_label=max_label)


def printtree(tree, indent='-', dict_tree={}, direct='L'):
    # 是否是叶节点

    if tree.results != None:
        print(tree.results)

        dict_tree = {direct: str(tree.results)}

    else:
        # 打印判断条件
        print(str(tree.d) + ":" + str(tree.thre) + "? ")
        # 打印分支
        print(indent + "L->",)

        a = printtree(tree.lb, indent=indent + "-", direct='L')
        aa = a.copy()
        print(indent + "R->",)

        b = printtree(tree.rb, indent=indent + "-", direct='R')
        bb = b.copy()
        aa.update(bb)
        stri = str(tree.d) + ":" + str(tree.thre) + "?"
        if indent != '-':
            dict_tree = {direct: {stri: aa}}
        else:
            dict_tree = {stri: aa}

    return dict_tree


def classify(observation, tree):
    if tree.results != None:
        return tree.results
    else:
        v = observation[tree.d]
        branch = None

        if v > tree.thre:
            branch = tree.rb
        else:
            branch = tree.lb

        return classify(observation, branch)


def pruning(tree, alpha=0.1):
    if tree.lb.results == None:
        pruning(tree.lb, alpha)
    if tree.rb.results == None:
        pruning(tree.rb, alpha)

    if tree.lb.results != None and tree.rb.results != None:
        before_pruning = tree.lb.NH + tree.rb.NH + 2 * alpha
        after_pruning = tree.NH + alpha
        print('before_pruning={},after_pruning={}'.format(
            before_pruning, after_pruning))
        if after_pruning <= before_pruning:
            print('pruning--{}:{}?'.format(tree.d, tree.thre))
            tree.lb, tree.rb = None, None
            tree.results = tree.max_label


if __name__ == '__main__':
    iris = load_iris()
    X = iris.data
    y = iris.target

    permutation = np.random.permutation(X.shape[0])
    shuffled_dataset = X[permutation, :]
    shuffled_labels = y[permutation]

    train_data = shuffled_dataset[:100, :]
    train_label = shuffled_labels[:100]

    test_data = shuffled_dataset[100:150, :]
    test_label = shuffled_labels[100:150]

    tree1 = buildtree(train_data, train_label, method='Gini')
    print('=============================')
    tree2 = buildtree(train_data, train_label, method='GainEnt')

    a = printtree(tree=tree1)
    b = printtree(tree=tree2)

    true_count = 0
    for i in range(len(test_label)):
        predict = classify(test_data[i], tree1)
        if predict == test_label[i]:
            true_count += 1
    print("CARTTree:{}".format(true_count))
    true_count = 0
    for i in range(len(test_label)):
        predict = classify(test_data[i], tree2)
        if predict == test_label[i]:
            true_count += 1
    print("C3Tree:{}".format(true_count))

    #print(attribute_based_on_Giniindex(X[49:51, :], y[49:51]))
    from pylab import *
    mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
    mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像时负号'-'显示为方块的问题
    import treePlotter
    import matplotlib.pyplot as plt
    treePlotter.createPlot(a, 1)
    treePlotter.createPlot(b, 2)
    # 剪枝处理
    pruning(tree=tree1, alpha=4)
    pruning(tree=tree2, alpha=4)
    a = printtree(tree=tree1)
    b = printtree(tree=tree2)

    true_count = 0
    for i in range(len(test_label)):
        predict = classify(test_data[i], tree1)
        if predict == test_label[i]:
            true_count += 1
    print("CARTTree:{}".format(true_count))
    true_count = 0
    for i in range(len(test_label)):
        predict = classify(test_data[i], tree2)
        if predict == test_label[i]:
            true_count += 1
    print("C3Tree:{}".format(true_count))

    treePlotter.createPlot(a, 3)
    treePlotter.createPlot(b, 4)
    plt.show()

附上treePloter.py

import matplotlib.pyplot as plt

# 定义文本框和箭头格式
decisionNode = dict(boxstyle="round4", color='#3366FF')  # 定义判断结点形态
leafNode = dict(boxstyle="circle", color='#FF6633')  # 定义叶结点形态
arrow_args = dict(arrowstyle="<-", color='g')  # 定义箭头

# 绘制带箭头的注释


def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
                            xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)


# 计算叶结点数
def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        else:
            numLeafs += 1
    return numLeafs


# 计算树的层数
def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth:
            maxDepth = thisDepth
    return maxDepth


# 在父子结点间填充文本信息
def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
    yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center",
                        ha="center", rotation=30)


def plotTree(myTree, parentPt, nodeTxt):
    numLeafs = getNumLeafs(myTree)
    depth = getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) /
              2.0 / plotTree.totalW, plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)  # 在父子结点间填充文本信息
    plotNode(firstStr, cntrPt, parentPt, decisionNode)  # 绘制带箭头的注释
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff,
                                       plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD


def createPlot(inTree, index=1):
    fig = plt.figure(index, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5 / plotTree.totalW
    plotTree.yOff = 1.0
    plotTree(inTree, (0.5, 1.0), '')

剪枝处理

这两种方法构建的决策树都存在一个过拟合的问题，需要通过剪枝处理以提高其泛化能力，我们这里使用一个惩罚函数来衡量过拟合程度：
$C_{alpha }(T)=sum_{t=1}^{T}N_{t}H_{t}+alpha left | T right |$
其中T为叶节点的个数即为模型复杂度， $α$ 为惩罚参数， $N_{t}$ 为训练时叶节点处的样本数， $H_{t}$ 为经验熵
$H_{t}(T)=-sum_{k}frac{N_{tk}}{N_{t}}log_{2}frac{N_{tk}}{N_{t}}$
剪枝的过程即为自下而上遍历决策树，寻找子节点均为叶节点的节点，然后计算剪枝前后惩罚函数是否变小，若变小则剪枝，将该节点的输出设为样本中同种最多的类别。
下图展示了上面程序输出的剪枝前后2个决策树的变化，其中{2：2.45？}表示属性2中小于2.45的走左边，否则走右边，训练集依旧是iris中随机100个样本，测试集为剩下的50个样本，剪枝前后以及不同决策树最后的准确率都为96%
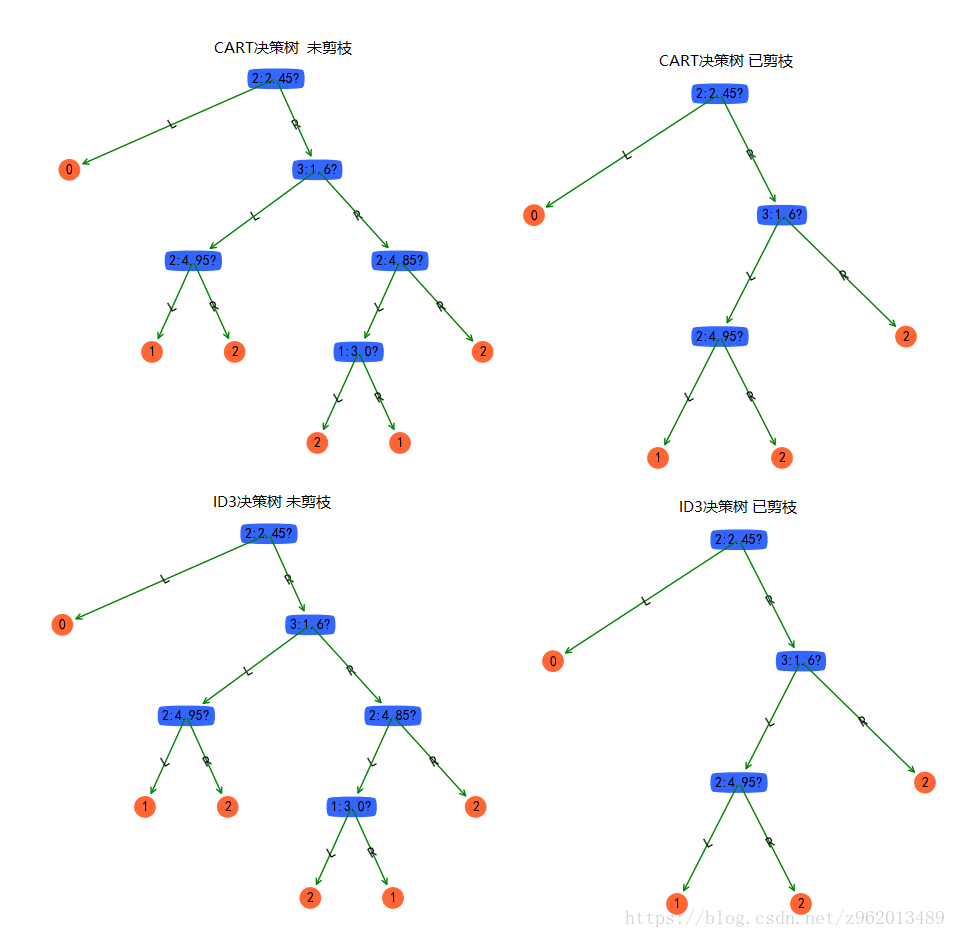
这里写图片描述

预测概率

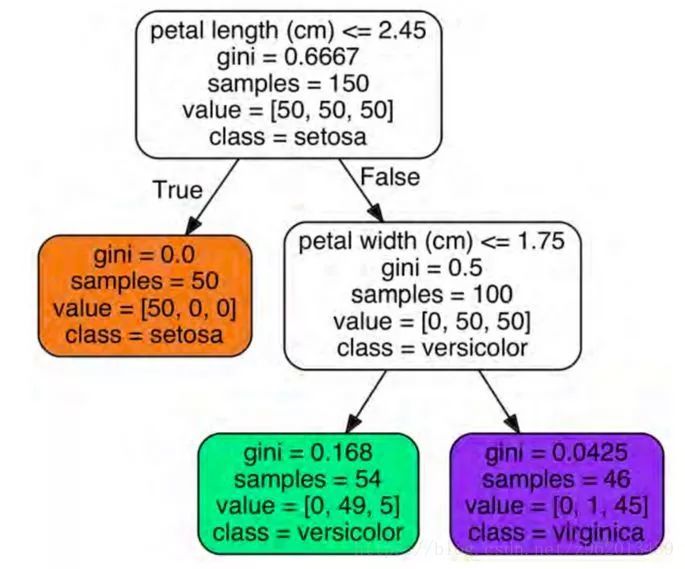
在这里插入图片描述
决策树还可以估计实例属于特定类 k 的概率：首先遍历树来找到此实例的叶子节点，然后返回该节点中类 k 的训练实例的比率。例如，假设你已经找到一朵花长 5厘米，宽 1.5 厘米的花朵。相应的叶子节点是深度为 2 的左节点，因此决策树应该输出以下概率：Iris-Setosa（0/54）为 0％，Iris-Versicolor为 (49/54)，即 90.7％， Iris-Virginica (5/54)，即 9.3 ％。当然，如果你让它预测类别，它应该输出Iris-Versicolor（类别 1），因为它具有最高的概率。

参考：
《机器学习》周志华
https://blog.csdn.net/csqazwsxedc/article/details/65697652
https://zhuanlan.zhihu.com/p/20794583
http://m.elecfans.com/article/711145.html