一、理想采样

1.1 理想采样流程分析

所谓的理想采样，就是利用间隔为 $T_s$ 的单位冲激串序列和输入的连续时间信号相乘。可以用下面的框图来表示：

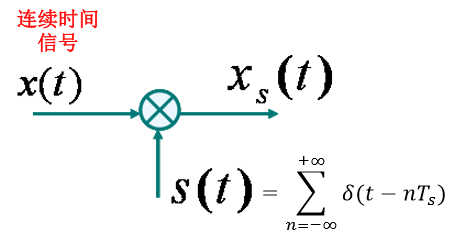
其中，$T_s$ 就是我们所说的采样周期。在时域上，这个框图用信号波形可以这样表述：

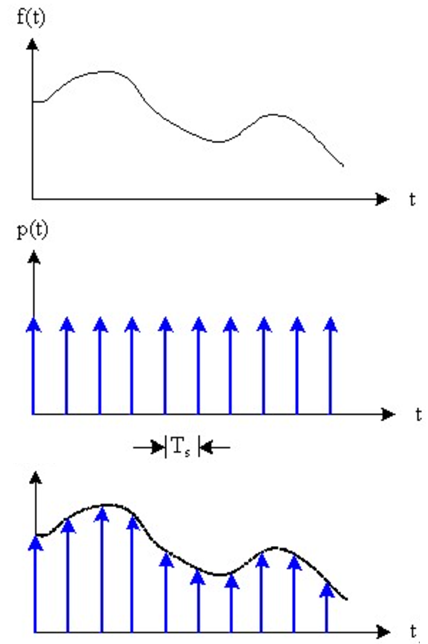
刚刚我们所表示的这种理想采样，在频域上可以这样画：

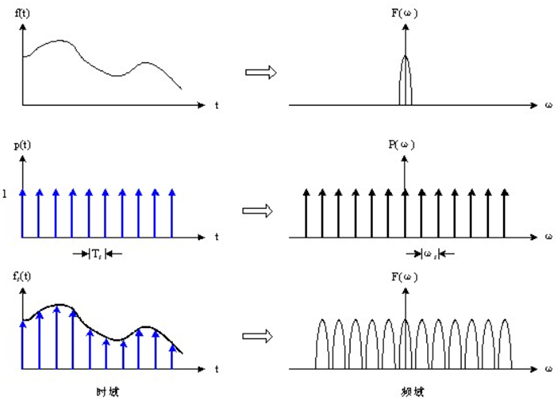
其中，值得注意的是，单位冲激串序列 ${\sum }_{n=-\infty }^{+\infty }\delta (t-n{T}_s)$ 的傅里叶变换（参照周期信号的傅里叶变换）是 $P(\omega )$，其幅度应该是 $\frac{2\pi }{T_s}$，我们能看到理想采样的过程，其实本质上就是原始信号频谱以 $T_s$ 为周期做了一个周期延拓。

1.2 如何从理想采样中恢复原始信号？

其实大家也看到了，通过频域分析，我们发现理想采样的过程，其实本质上就是原始信号频谱以 $T_s$ 为周期做了一个周期延拓。我们用下面这个更加细致的图分析：

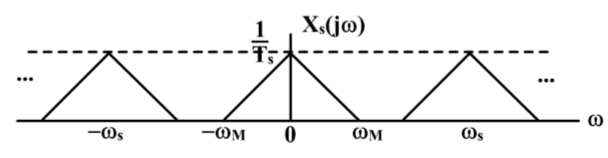
上图是经过理想采样之后信号的频谱，我们看到：每一个“三角形” 之间都是有一定的空隙的。而我们知道：中间那个“三角形”（请先允许我用 “三角形” 这样不够准确的华语来暂时描述原始信号的频谱）就是原信号的频谱。那么可以想到使用下面这样的低通滤波器：

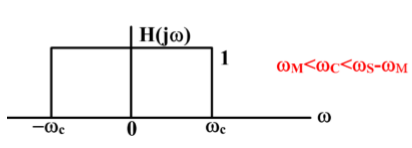
但是我们要确保这个理想低通滤波器的介质频率 ${\omega }_c$ 应该要比 ${\omega }_M$ 大（这样才能让原信号的所有频率成分都顺利通过），但是又要小于 ${\omega }_s-{\omega }_M$（也就是说，这个理想低通滤波器不能让上图旁边两个“三角形” 有能够通过的余地）。那么当经过理想采样的信号通过这个 filter 的频谱如下图所示：

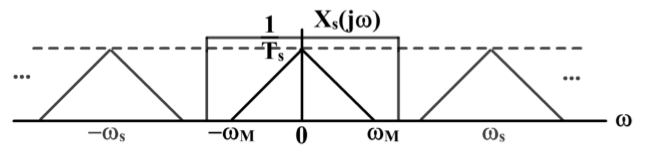
那么经过滤波器之后得到的信号频谱就是：

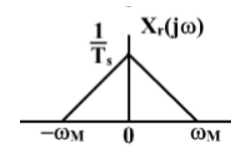
那么这不就是原信号的频谱嘛！

1.3 频谱混叠和奈奎斯特采样定律

那么，问题来了：我们所选取的这个单位冲激串序列的间隔有什么要求呢？$T_s$ 大一点小一点对采样会造成什么影响呢？这个问题在时域上不能直观的表示，我们转到频域去分析。

通过刚刚的图我们也看到，我们加的理想低通滤波器只希望中间的 “三角形” 可以通过，而两边的 “三角形” 的任何成分都不希望通过滤波器。

那么着意味着：成功恢复采样信号的第一条准则就是：这个被采样信号一定是带限的！即频谱宽度有限
试想一下，如果是一个带宽无限的信号，那么无论你用什么滤波器，旁边的 “三角形” 一定有成分通过滤波器，这样必然会造成频率混叠。如果原信号是一个带宽无限的信号，那么对他的采样就得先让他经过一个抗混叠滤波器（截取一部分得频谱）

另外，我们也看到了：上面的 ”三角形” 与 “三角形” 之间都是有一定的间隔的。因此奈奎斯特采样定理的第二点内容就是：采样频率 $f_s$ 必须大于等于两倍的信号频率 $f_o$，即：$f_s\ge 2f_o$
不然会发生下面的情况：

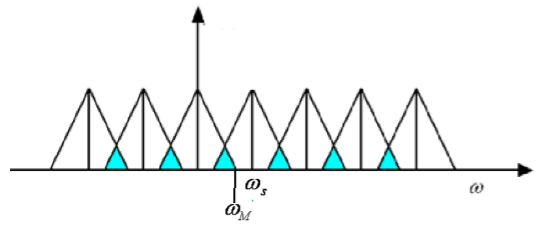
这样也是无法恢复出原信号的。因此必然掺杂了其他频率成分在里面。

总结一下，奈奎斯特采样定律包括了下面两条要求：

1. 这个被采样信号一定是带限的！即频谱宽度有限
2. 采样频率 $f_s$ 必须大于等于两倍的信号频率 $f_o$，即：$f_s\ge 2f_o$

二、利用内插由样本重建信号

2.1 理想带限内插

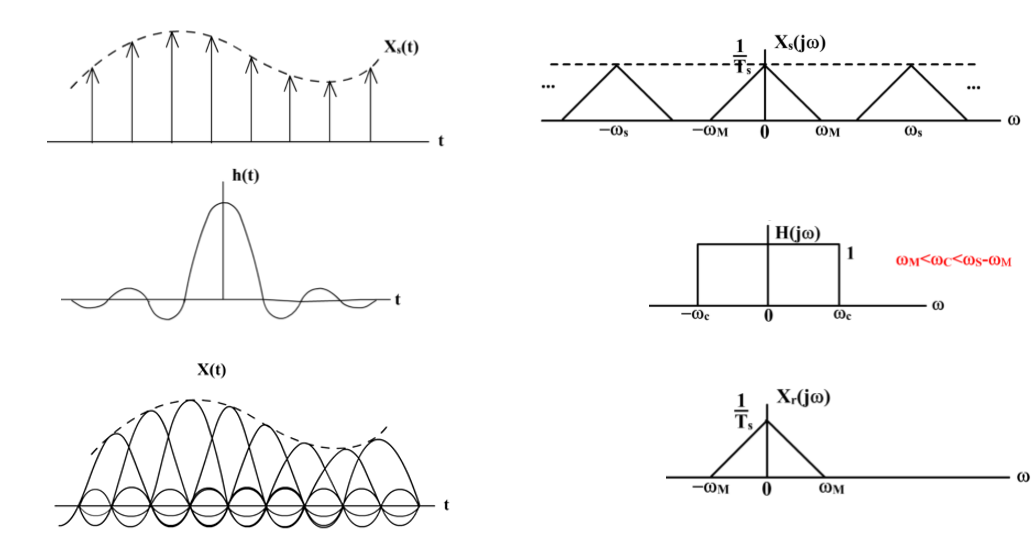
现在我们开始讨论如何从所采集到的样本中恢复原始信号。第一种就是理想带限内插。也即是让采样所得的信号通过理想低通滤波器（即上图所述的方法）。下面我们从时域和频域上看看是怎样的一个过程：

2.2 零阶保持内插

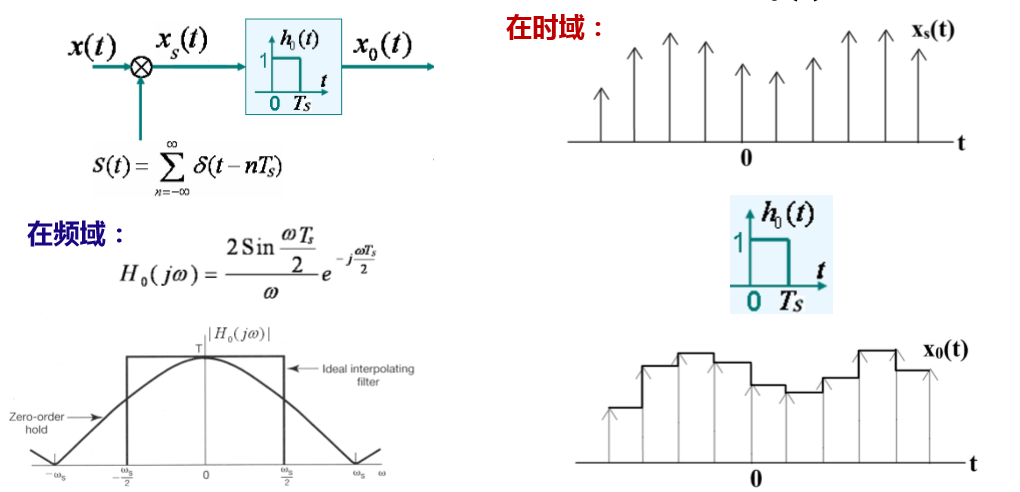
所谓零阶保持内插，在时域上所使用的信号就是在 0~$T_s$ 内幅度为1的门信号。我们来看看时频效果：

2.3 一阶保持内插

一阶保持内插在时域上所使用的信号就是一个 “三角形” 形状的信号，我们来看看：

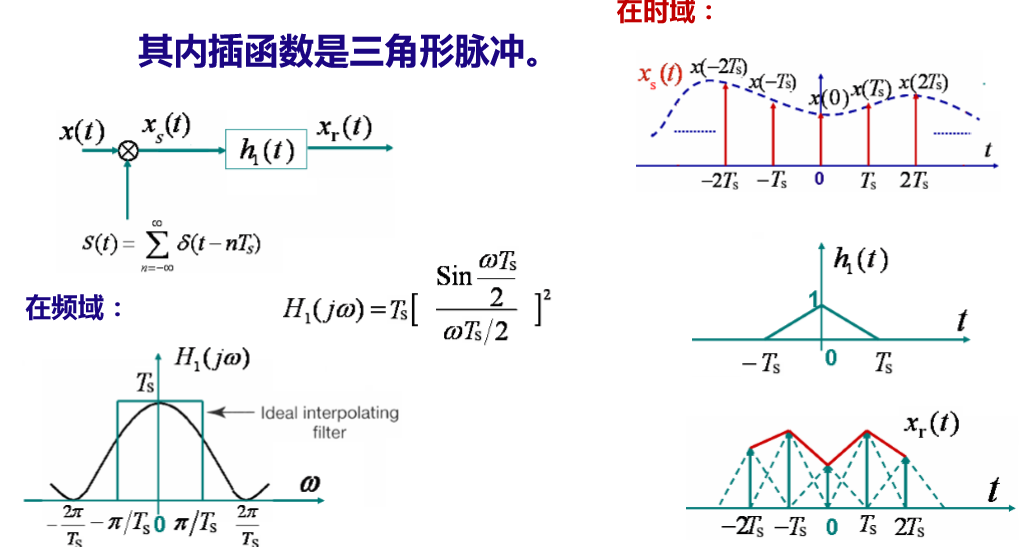
值得注意的是：在图像恢复领域，使用零阶保持可能会令图片出现像素化的情况；但是使用一阶保持会令图片更加平滑（但是视觉上会变得模糊）

OK，本次博文暂时就写这么多，下一篇将会是一篇短文，介绍一下连续时间信号的离散时间处理。哈哈听名字是不是觉得很绕口，没关系！我们下一次好好看看它的真面目！See you !

最后

以上就是真实大白为你收集整理的【信号与系统学习笔记】—— 采样与恢复（内插重建方法解析）一、理想采样二、利用内插由样本重建信号的全部内容，希望文章能够帮你解决【信号与系统学习笔记】—— 采样与恢复（内插重建方法解析）一、理想采样二、利用内插由样本重建信号所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。