VICTS（可变倾角连续横向枝节）天线的封闭表达式

参考文献

【1】Closed form expression for antenna patterns of the variable inclination continuous transverse stub,2010.
【2】Theoretical Model for patterns of VICTS Antenna.2017

写在开头

VICTS天线是在CTS天线基础之上发展来的，关于VICTS天线封闭表达式推导相关的论文不多，经过IEEE和知网的检索后只有两篇文章具有一定的参考价值，部分资料应该是Raytheon的一些秘密文件，不对外开放。所以本文章也只是基于第一篇文章做了一个总结和简单的复现，感兴趣的可以继续看看第二篇文章。
观看这篇文章需要对CTS天线有了一定的了解，有兴趣的可以参考相关论文。

正文

对与一个CTS天线而言，只能实现一个方向上的扫描，但是某些场景下我们不仅仅需要俯仰面的波束扫描，还希望可以在方位面实现波束扫描，因此，常采用的方式是为每个单元加上有源移相器，在源处就改变波的相位，最终使得叠加后方向图可以实现方位面上的波束扫描。但是，移相器会使得天线的成本和设计复杂度大大提高，因此基于这样的需求，有的学者提出了VICTS天线的设想，除了可以调整源的相位，也可以通过调整辐射缝隙的位置，也就是固定源与下层板的位置，通过旋转上层辐射缝隙的位置，使得辐射相位发生变化。

如下面两张俯视图所示，缝隙间距离为d，旋转角度为γ。


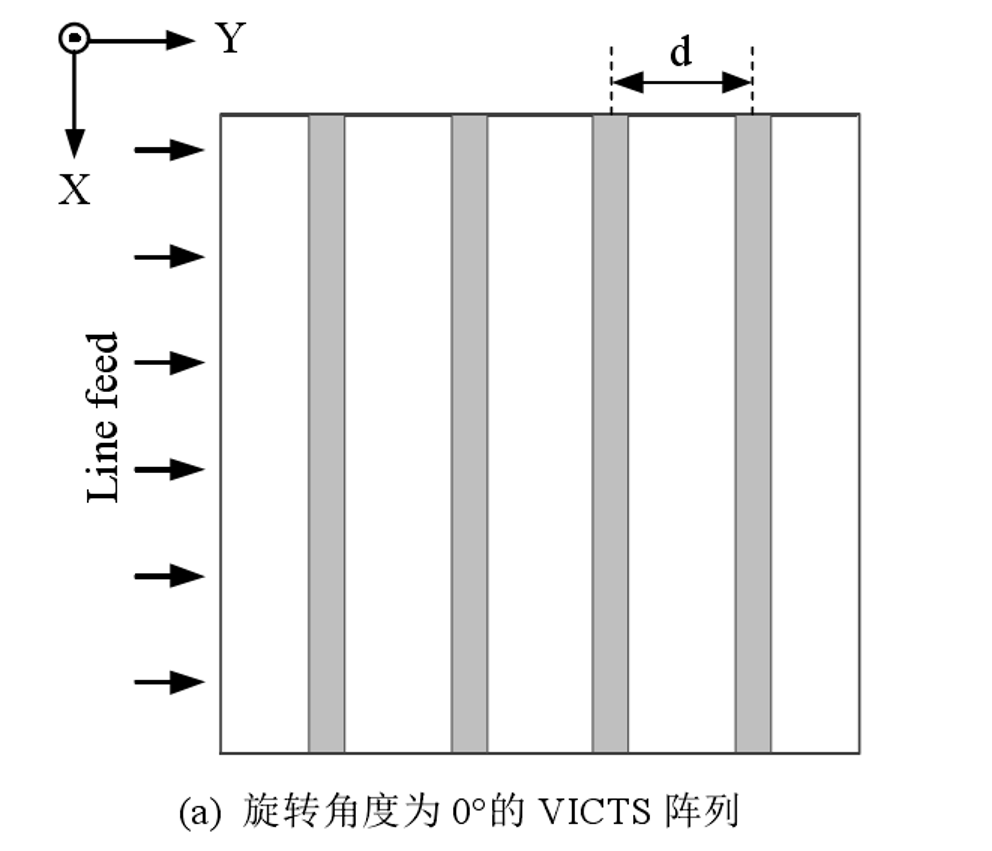
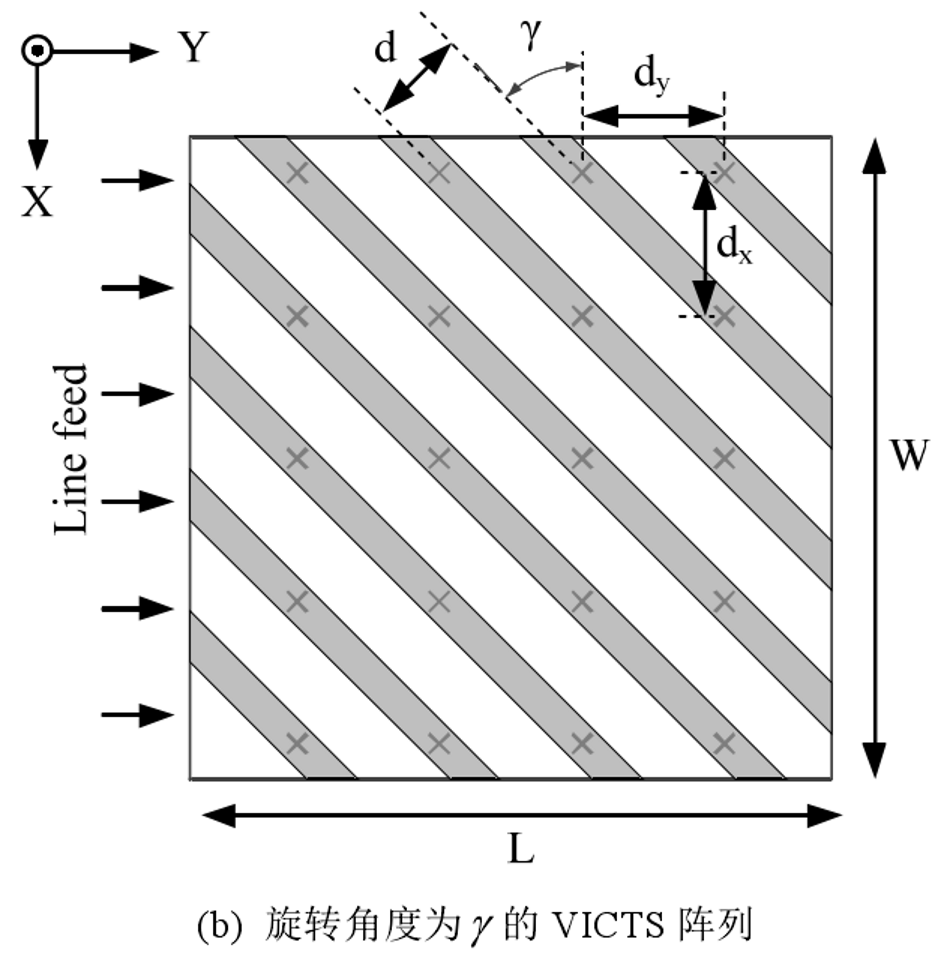
在检索到的两篇文章中，都是利用二维天线阵去拟合的思想，而2017年的文章又在2010年文章的基础上做了一定的改进。
对缝隙进行离散化处理，图(b)中每个×号都代表一个辐射点源的位置，若每个辐射点源的辐射均匀，则很容易推出整个阵列的阵因子表达式：

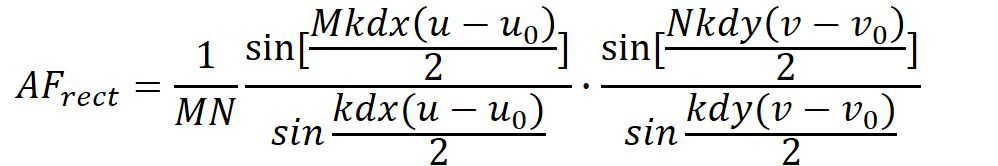
（有关阵列天线的阵因子推导可以参考《天线理论与技术》钟顺时，也可以B站观看储庆昕老师的《天线原理》课程视频）

上述表达式中：dx=d/sinγ，dy=d/cosγ；M，N分别为x方向和y方向上离散点源的个数；u，v表示远场观察点和x轴、y轴之间的方向余弦，u=sinθcosφ，v=sinθsinφ；kdx u0，kdy v0表示单元之间的激励相差。

很显然，该表达式的精确程度同我们所取点源的数目相关，因此我们将上述点源阵平移（-dx/2，dy/2），得到如下阵列：

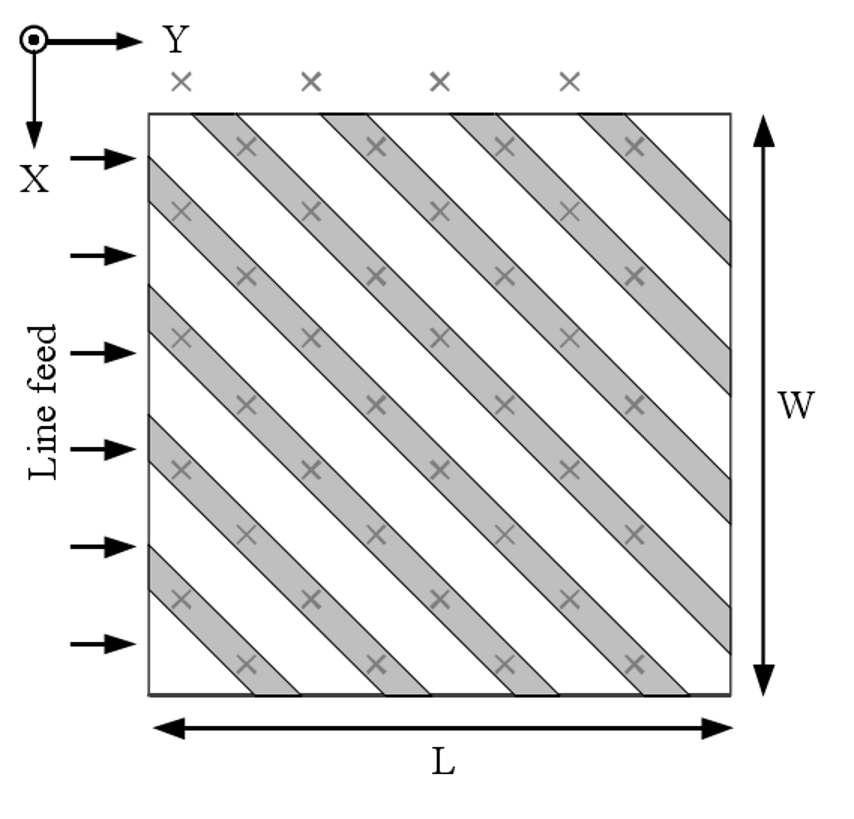
此阵列的阵因子表达式变为

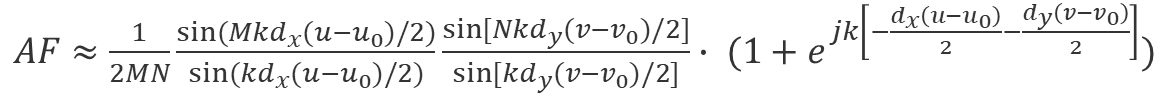
经过Q次平移（每次平移距离都是上一次的一半）可以得到

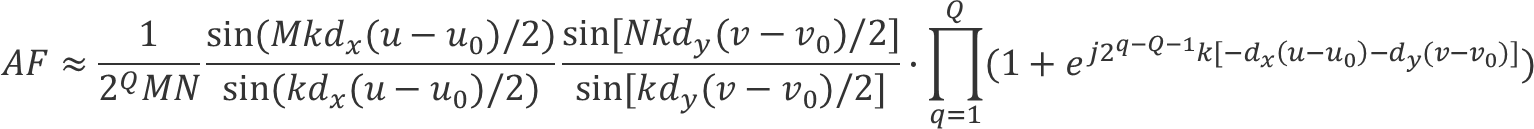
如果馈源沿y轴正方向馈入，那么等相位面与x轴平行，可以得到：

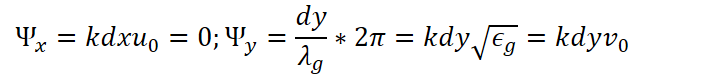
此时阵因子表达式则为

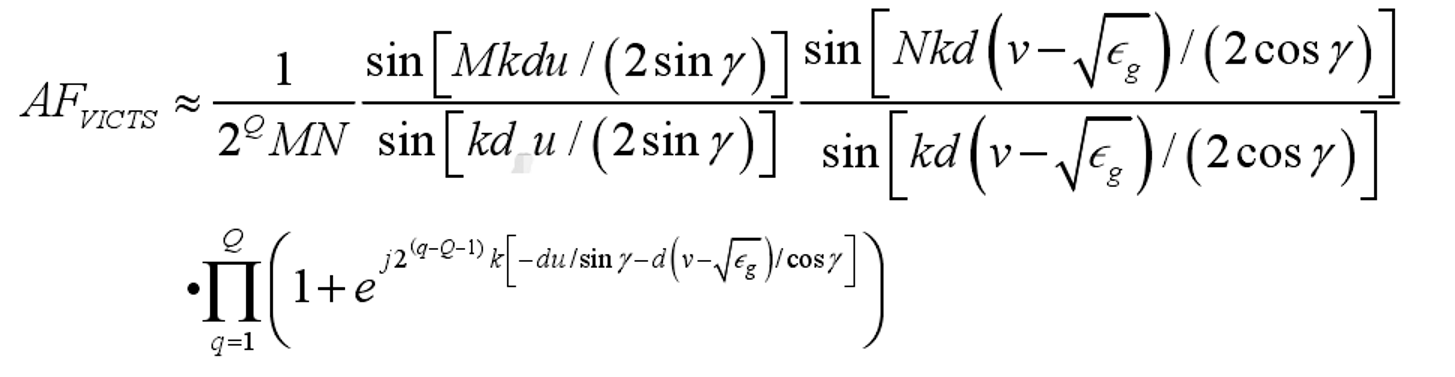
参考程序

clc
clear all
theta = 0.001*pi:0.001*pi:2*pi ;
phi = 0.001*pi:0.001*pi:2*pi ;
c = 3e8;
f = 1e9;
eg = 1.3;       %等效介电常数
lmda = c./f;
k=2.*pi./lmda;
d = 0.63*lmda./(eg)^0.5;
gama = pi.*(35/180);

dx = d./sin(gama);
dy = d./cos(gama);
M = 10;         
N = 10;

AF3 = ones(length(phi),length(theta));
[theta,phi]=meshgrid(theta,phi);

u = sin(theta).*cos(phi);       %方向余弦
v = sin(theta).*sin(phi);

AF1 = sin(M.*k.*dx.*u./2) ./ (M*sin(k.*dx.*u./2));
AF2 = sin(N.*k.*dy.*(v - eg^0.5)./2) ./ (N*sin(k.*dy.*(v - eg^0.5)./2));

Q = 3;

for q = 1 : Q
    AF3 = AF3 .* (1 + exp(i*(2^(q-Q-1)).*k.*(-d.*u./(sin(gama)) + d.*(v - eg^0.5) ./ (cos(gama)) ) ) );
end
AF = AF1.*AF2.*AF3./(2^Q);      %阵因子总表达式
% AF = AF.* sin(theta);
AF = abs(AF);

% figure(1);
% surf(theta(1,:),phi(:,1),abs(AF));
% shading flat;
% colorbar;
% xlabel('theta');
% ylabel('phi');
% zlabel('幅度');

figure(2);
polar(theta(1,:),AF(1,:));

最后

以上就是敏感电话为你收集整理的VICTS（可变倾角连续横向枝节）天线的封闭表达式的全部内容，希望文章能够帮你解决VICTS（可变倾角连续横向枝节）天线的封闭表达式所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。