1.傅里叶级数和傅里叶变换

笔记来源：fourier series and fourier transform

1.1 正弦波

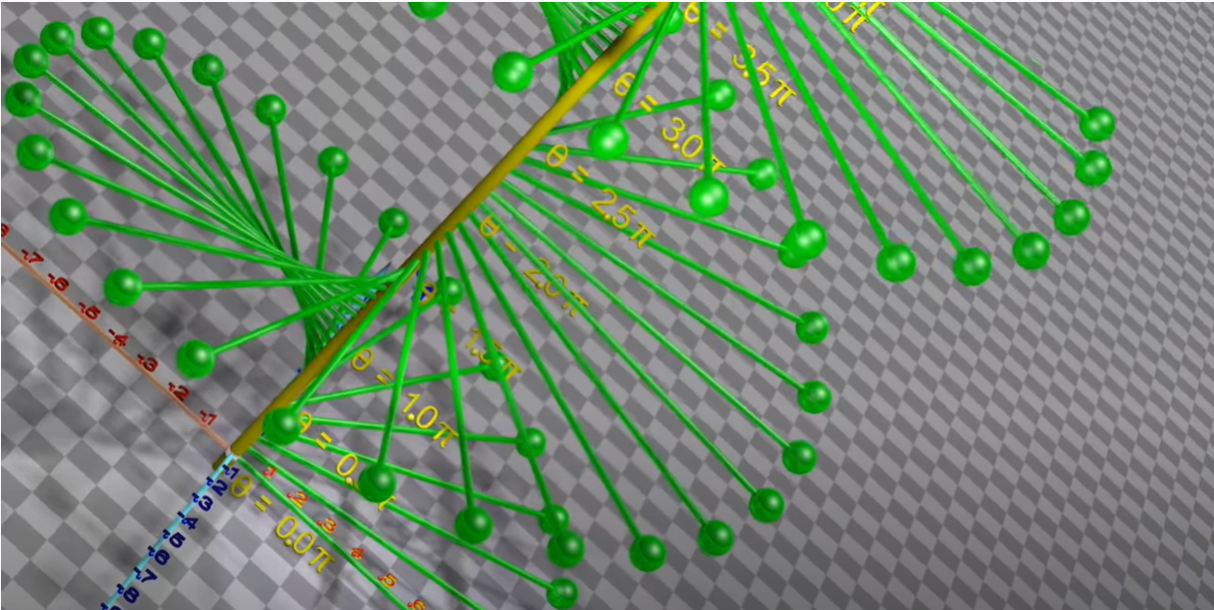
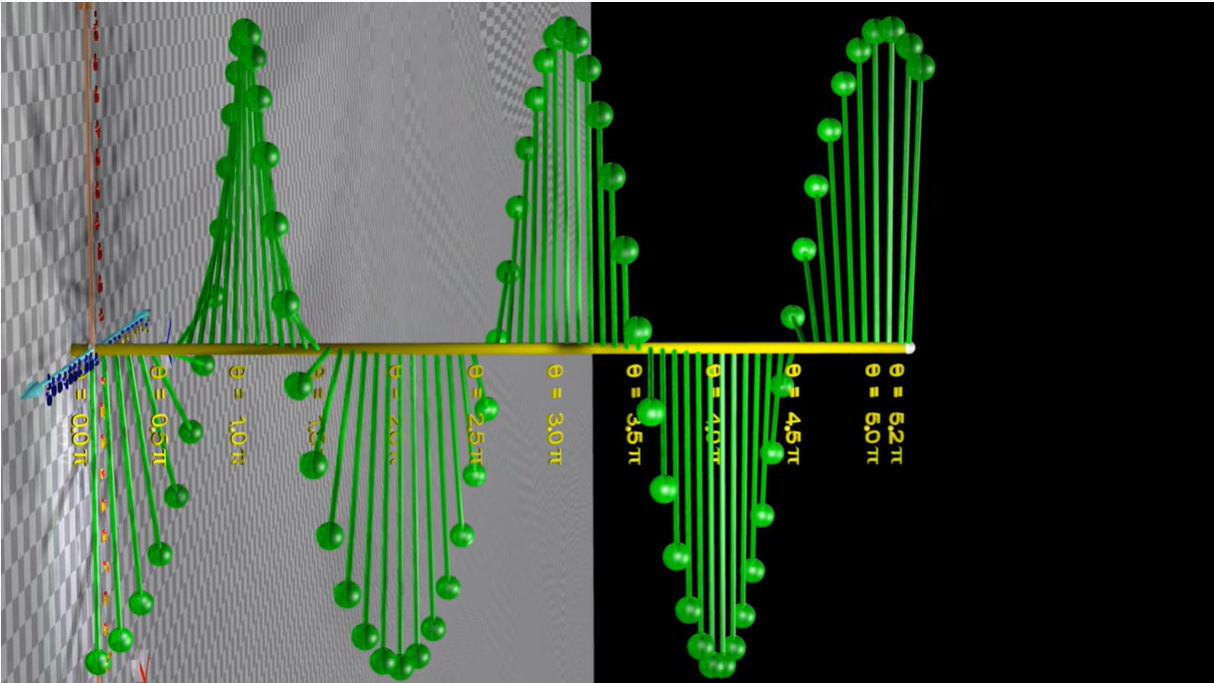
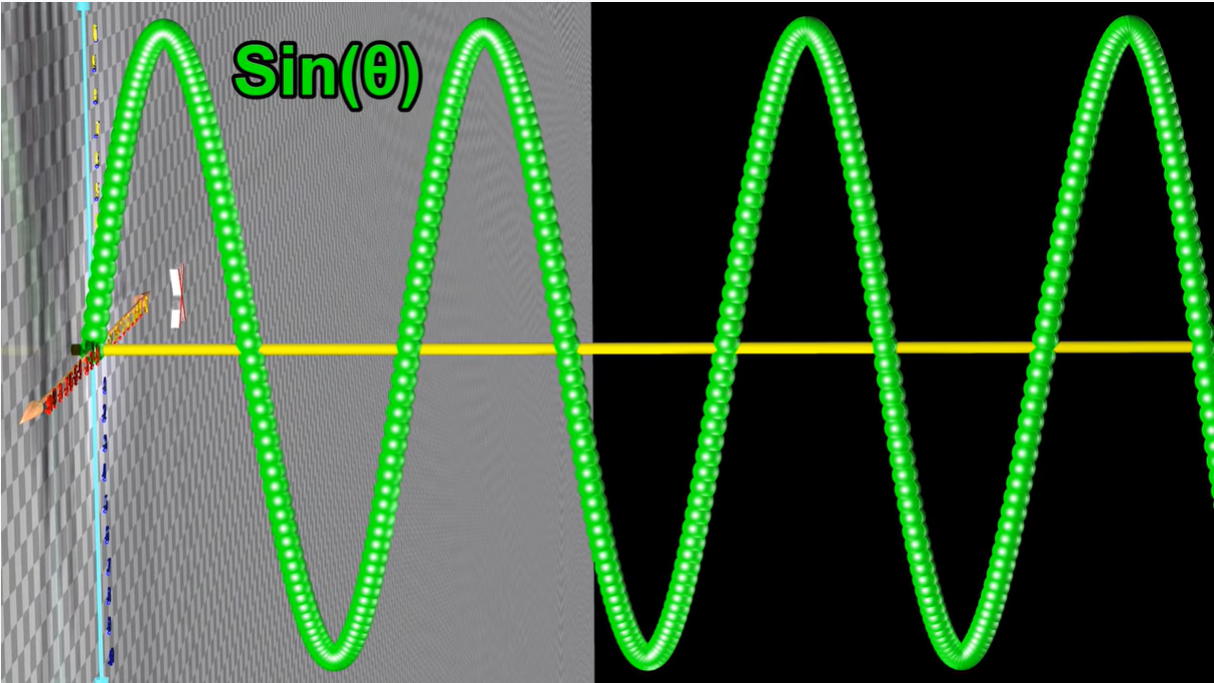
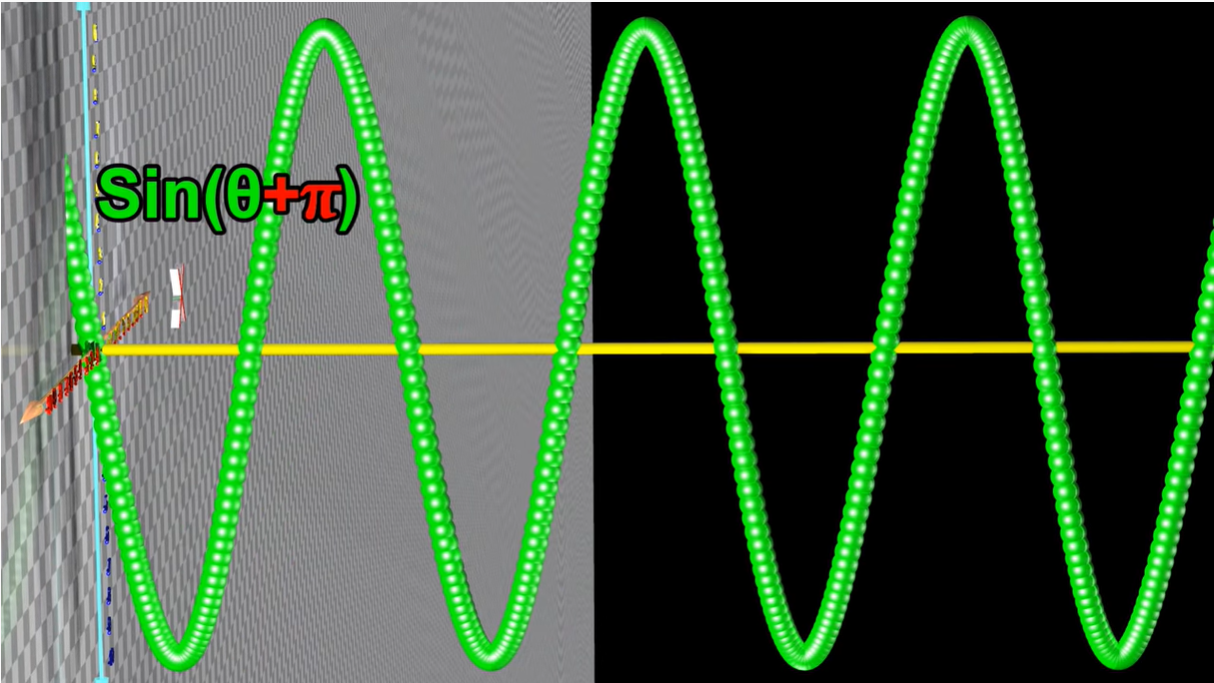
1.1.1 正弦波相位

改变相位（对应上面第一幅动图中的杆，其初始位置）

1.1.2 正弦波振幅

改变振幅（对应上面第一幅动图中的杆，其长度大小）

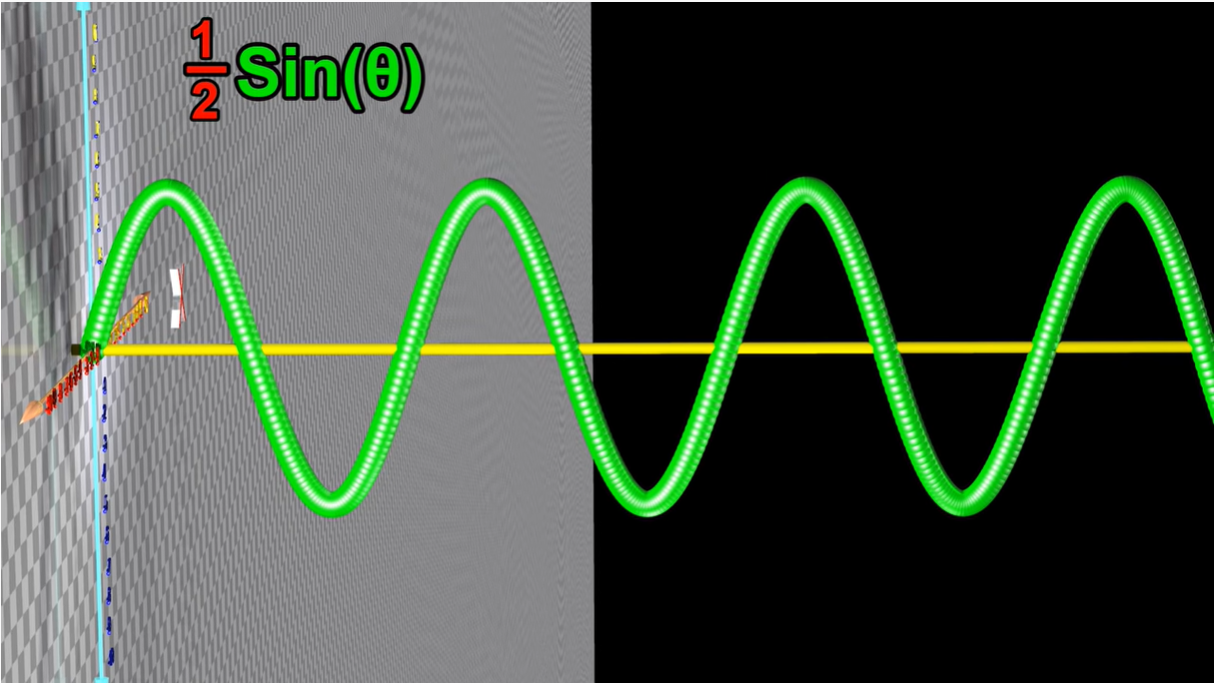
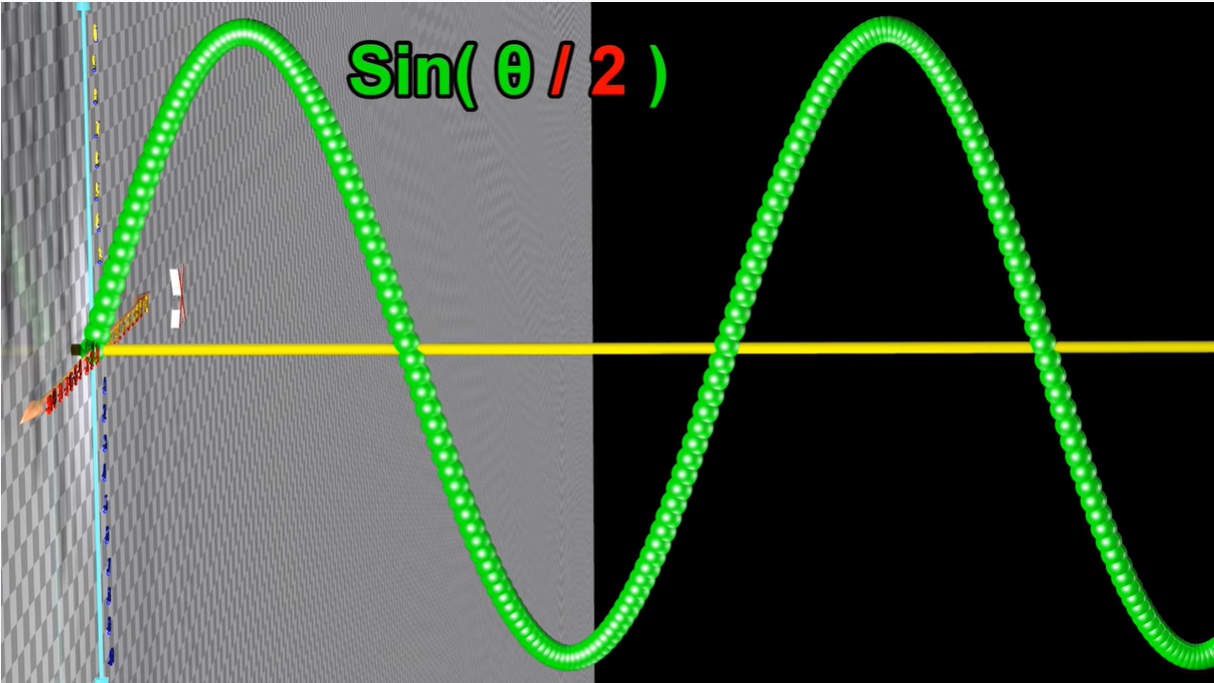
1.1.3 正弦波频率

改变频率（对应上面第一幅动图中的杆，其转动的频率）

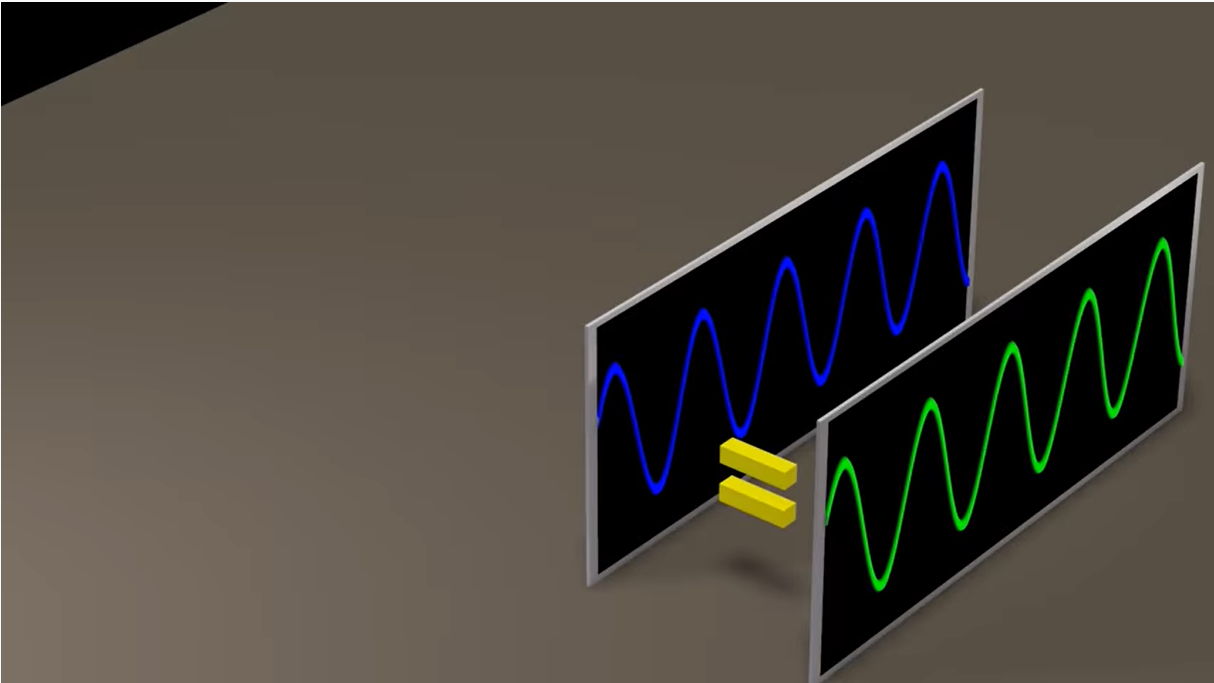
1.2 两种相同频率、不同振幅的正弦波叠加

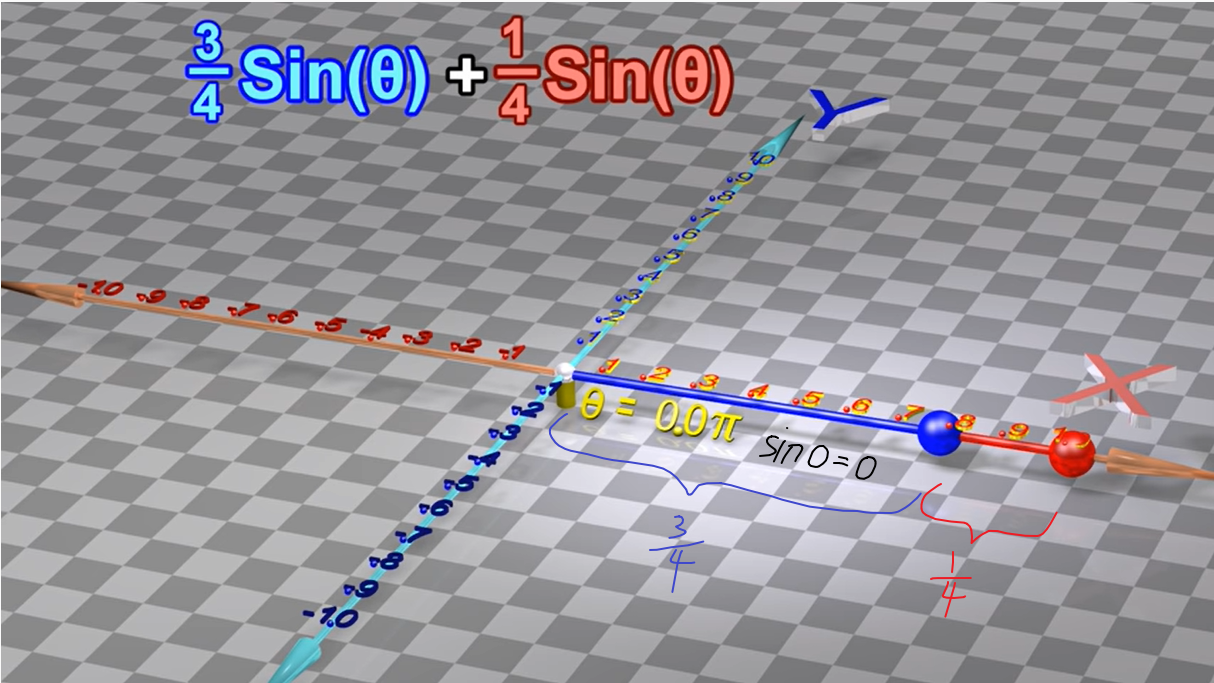
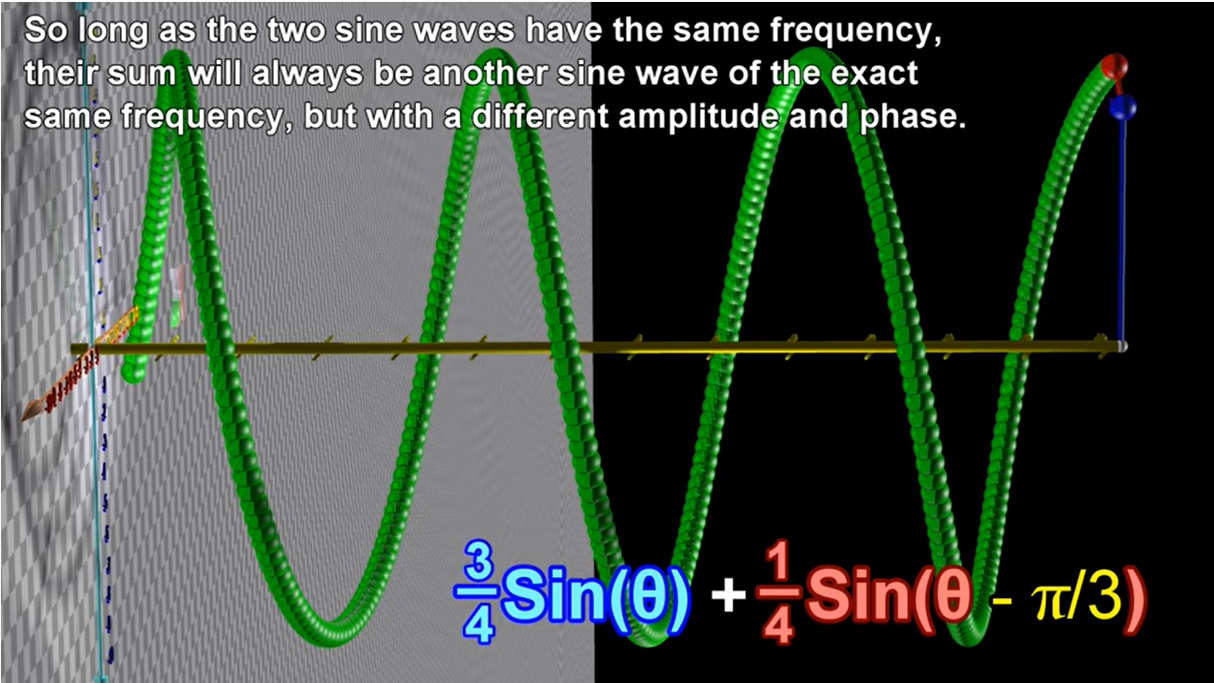
1.3 两种相同频率、不同振幅、不同相位的正弦波叠加

假设两个正弦函数有不同的相位

两个相同频率的正弦波之和 = 另一个有相同频率的正弦波（此正弦波与前面两个正弦波的振幅和相位不相同）

1.4 两个不同频率、不同振幅的正弦波叠加

假设两个正弦波有不同频率（似乎是转动频率）

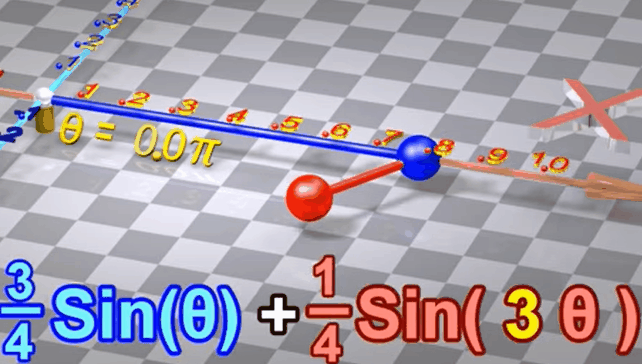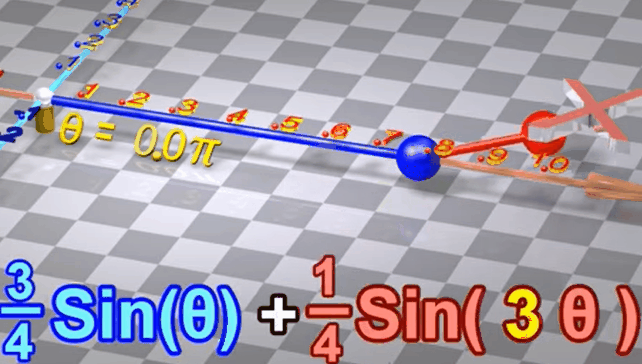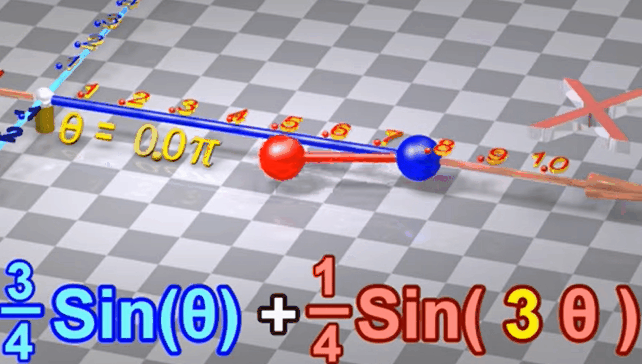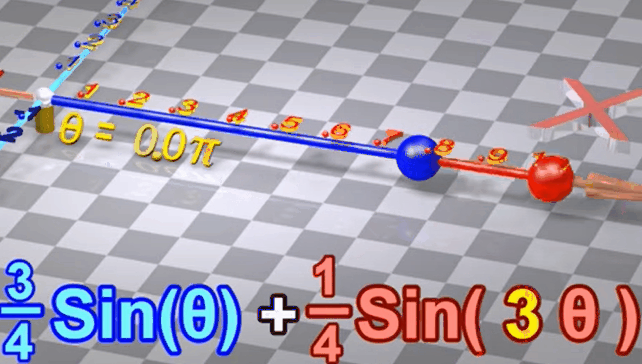
蓝色转一圈的过程中红色转三圈

将两个不同频率的正弦波叠加，得到的结果不再是正弦波

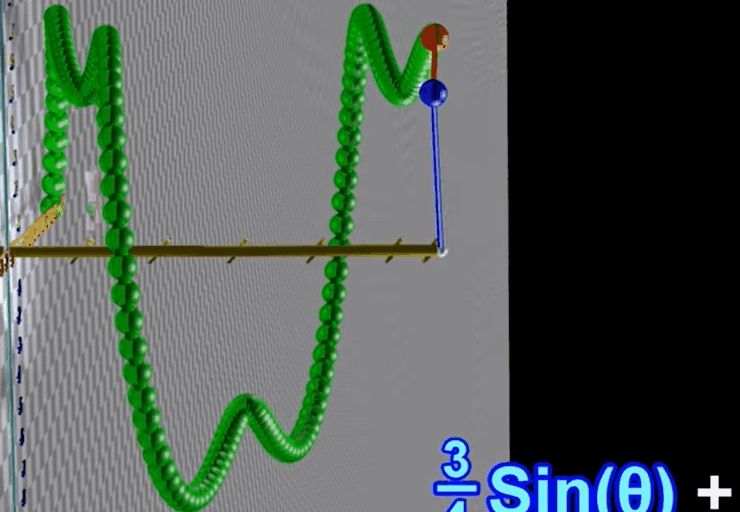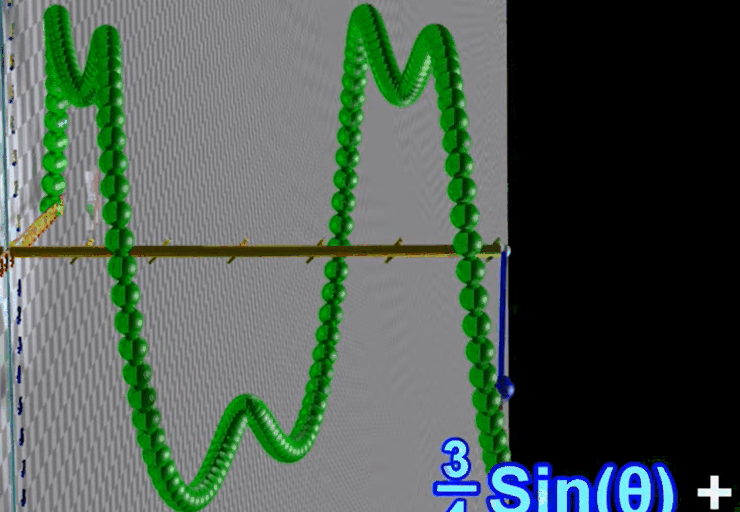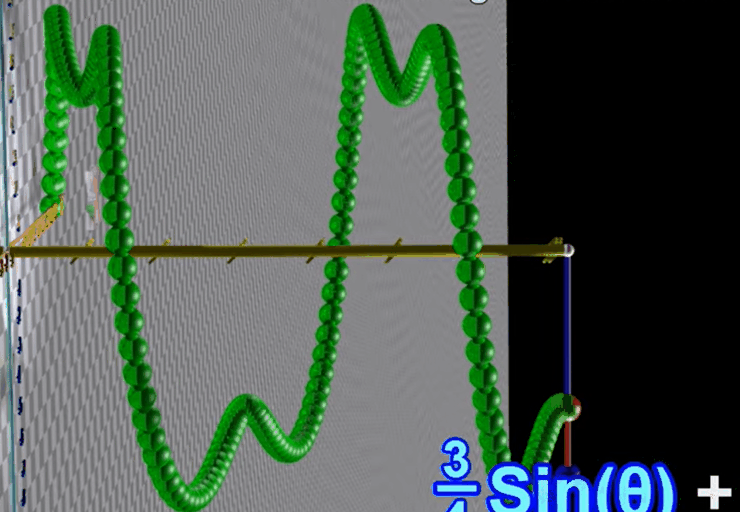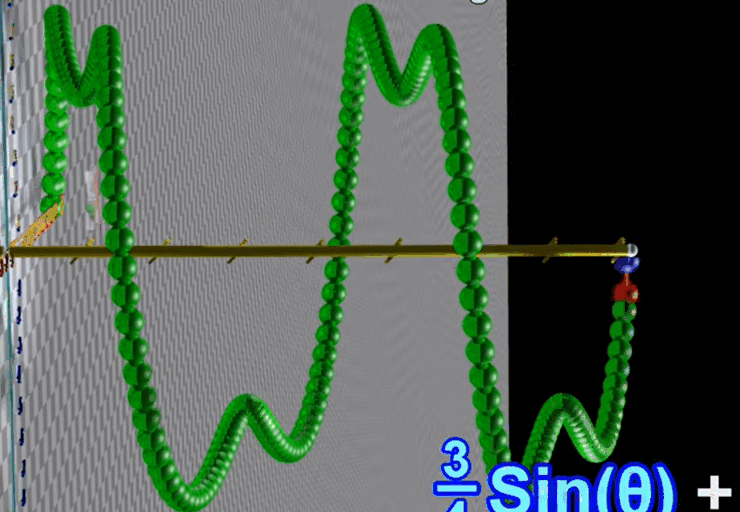
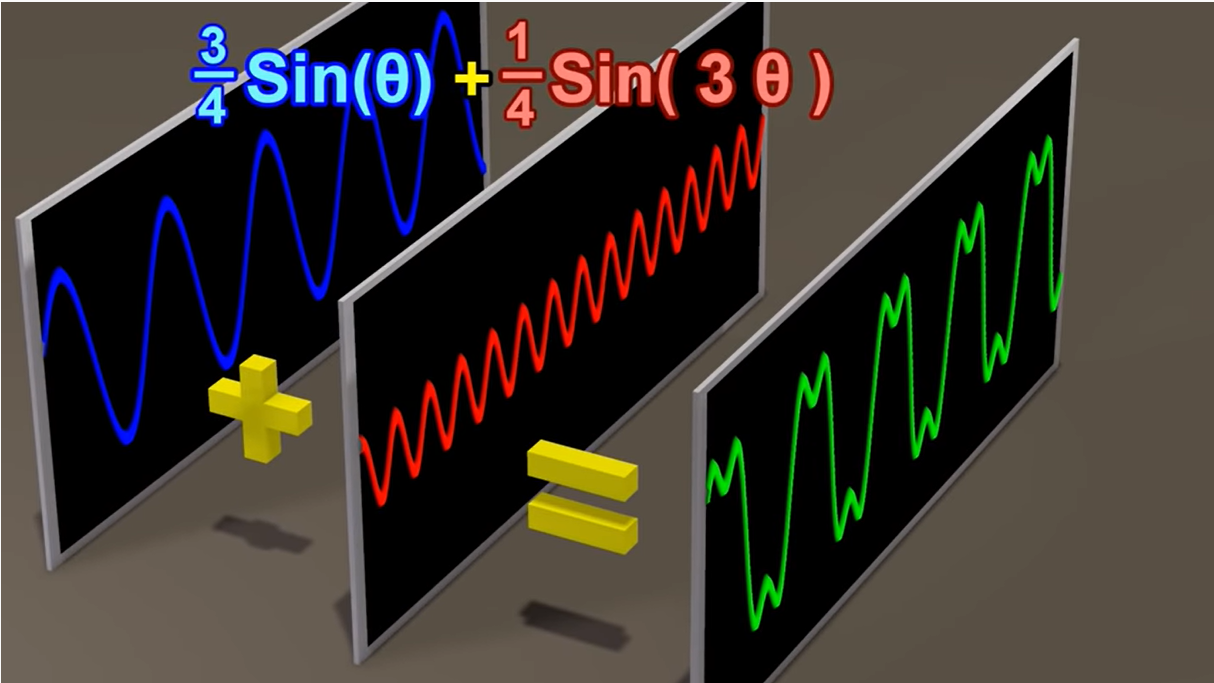
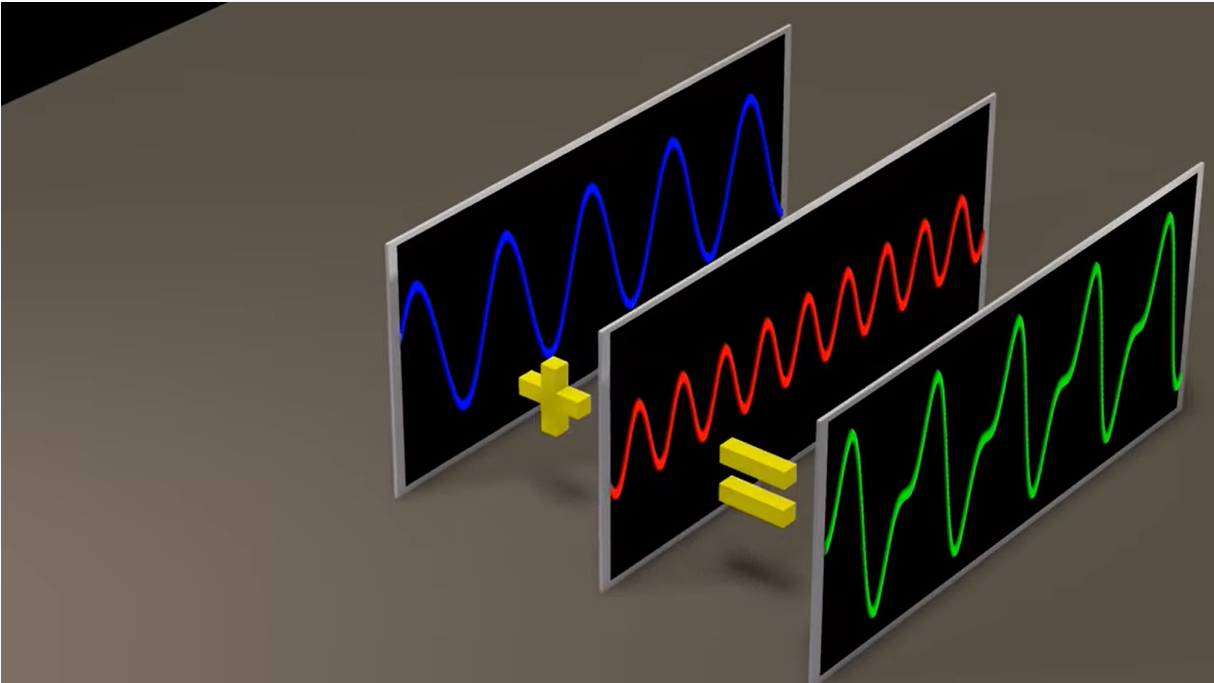
1.5 三种不同频率、不同振幅的正弦波叠加

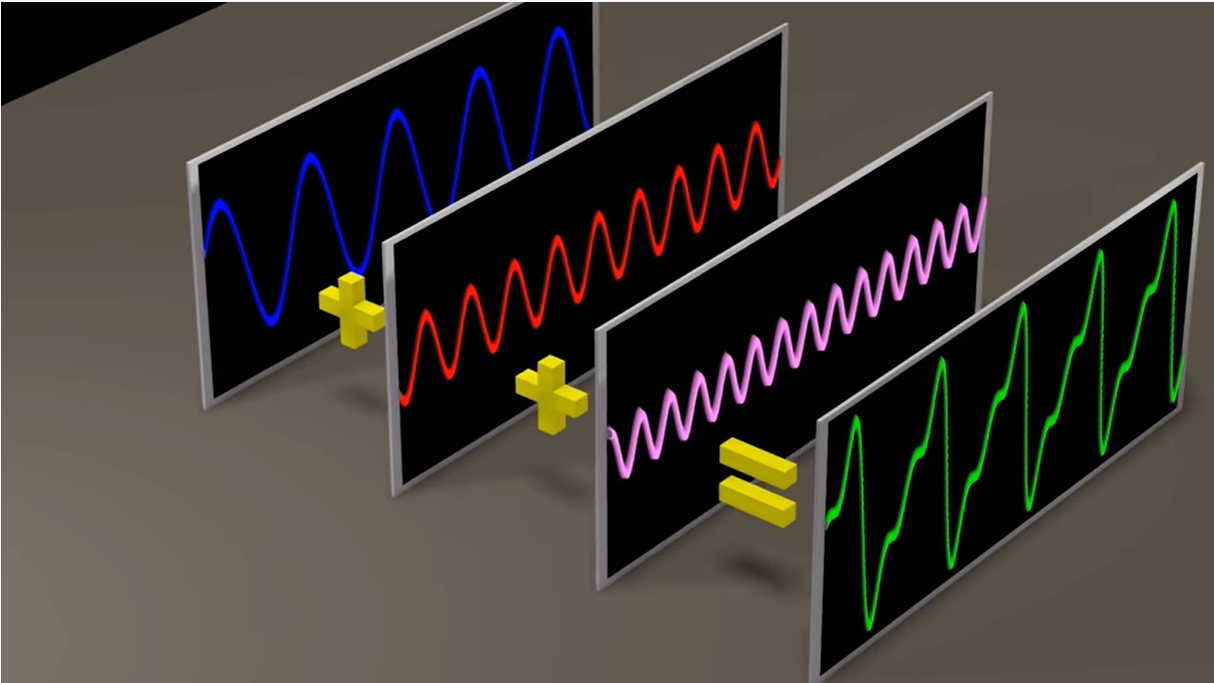
1.6 五种相同相位、不同频率、不同振幅的正弦波叠加

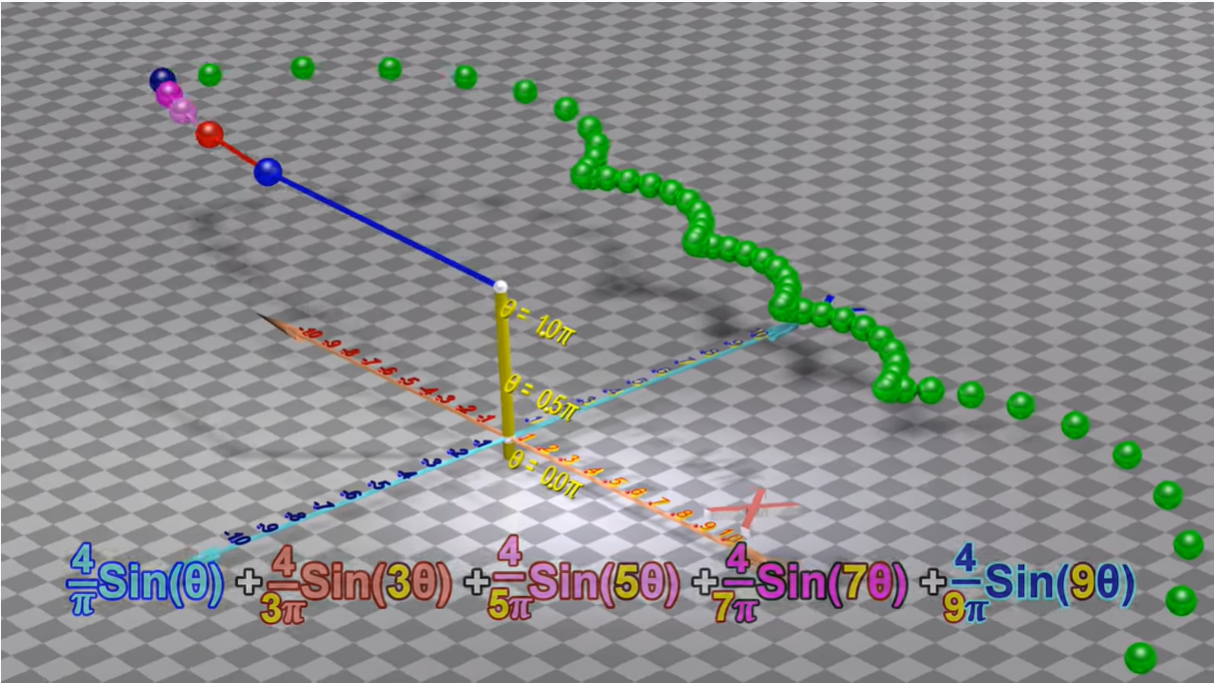
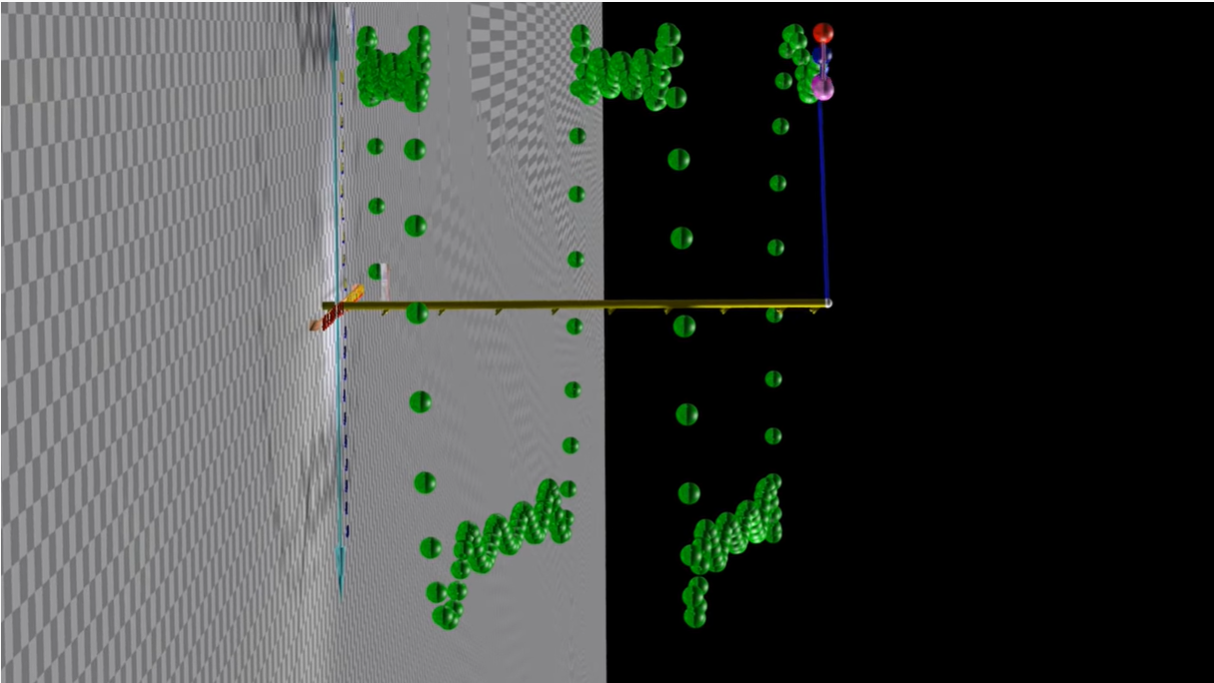
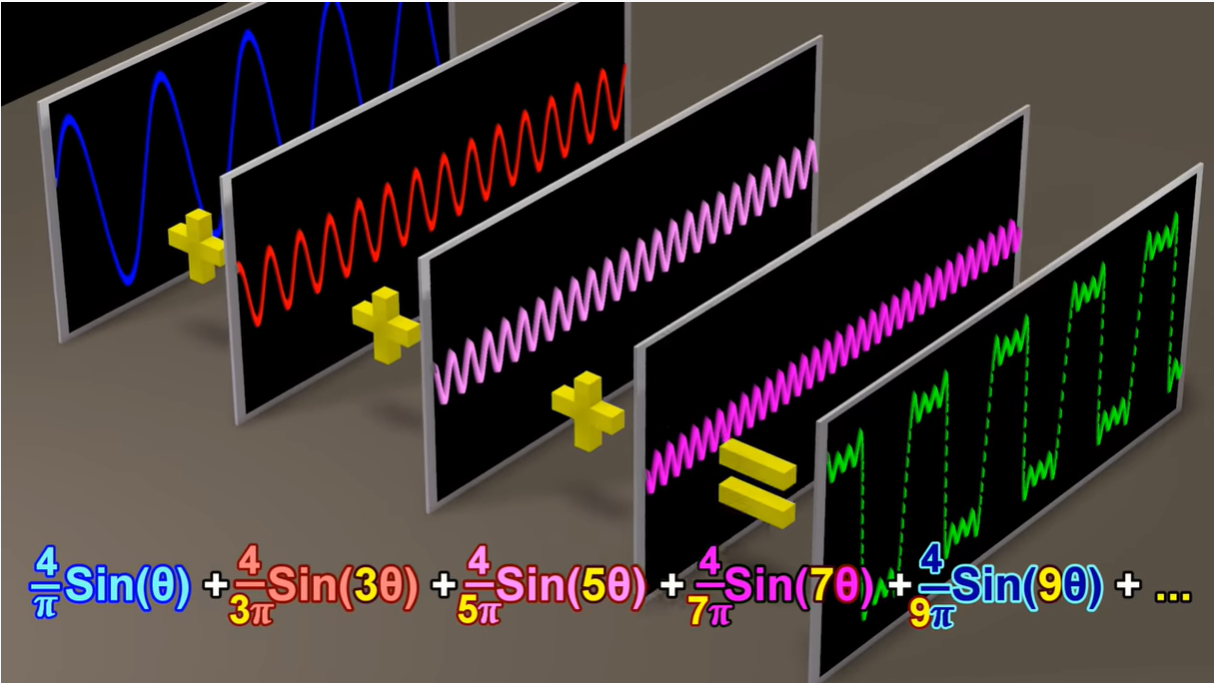
随着无数相同相位、不同频率、不同振幅的正弦波的叠加，图像会大致呈现如下图
这里的无数个正弦函数，其实就对应了傅里叶级数

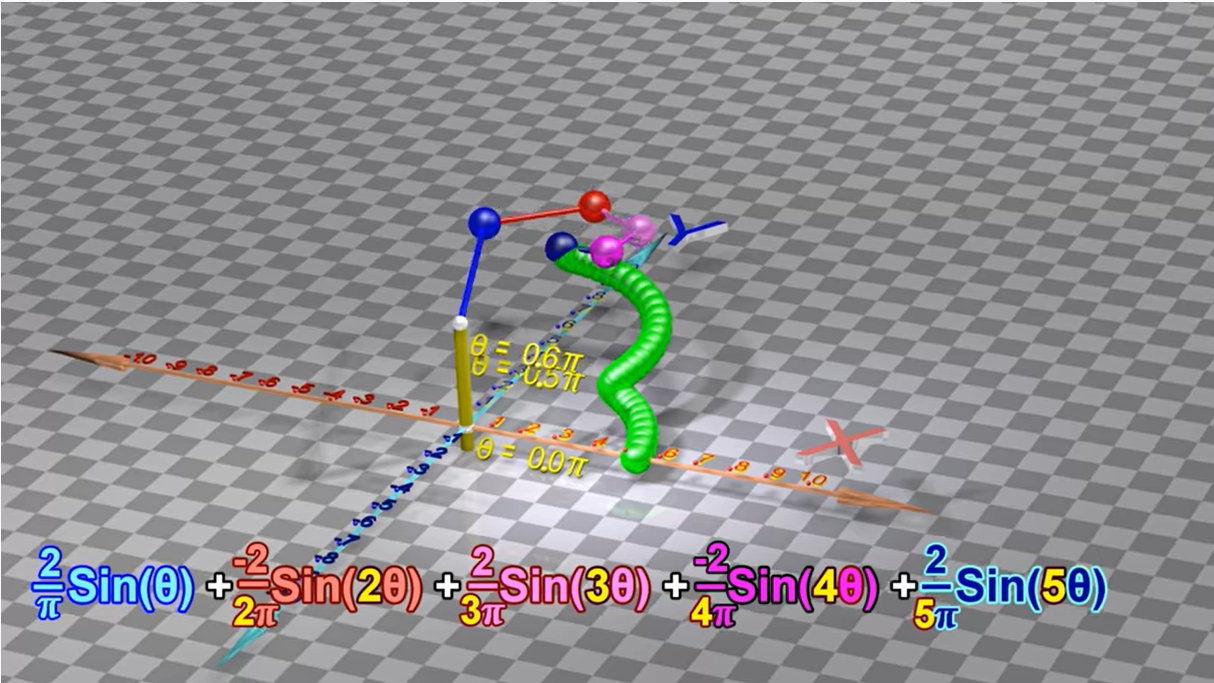
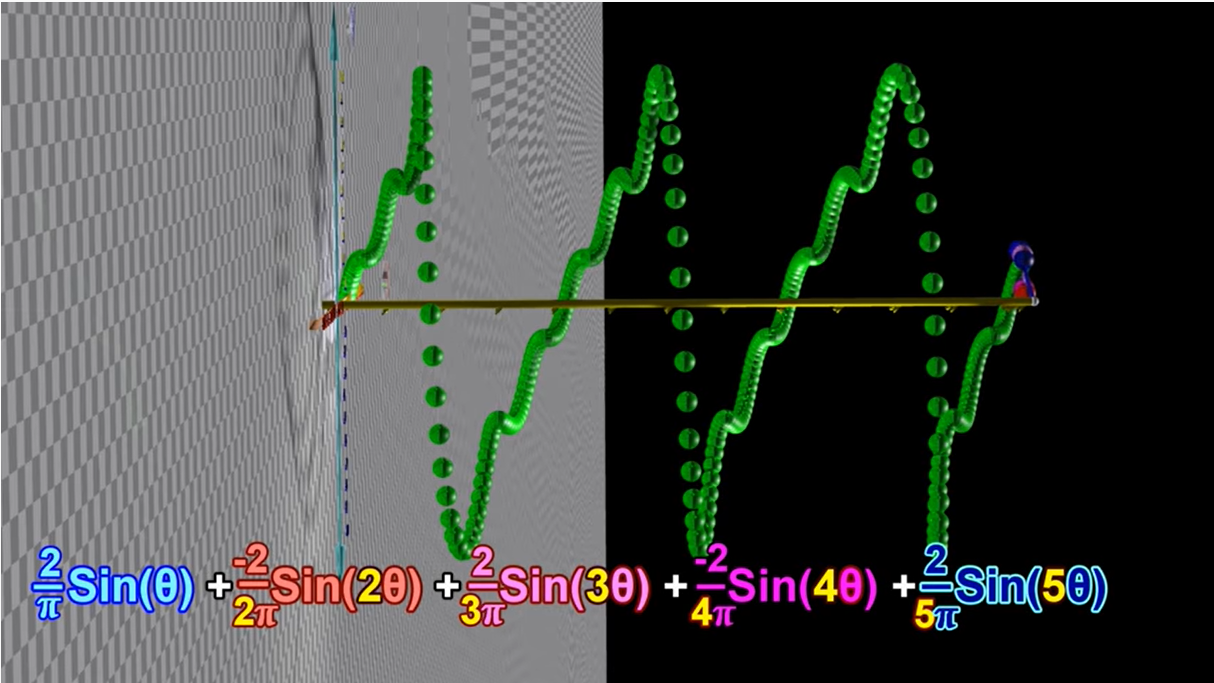
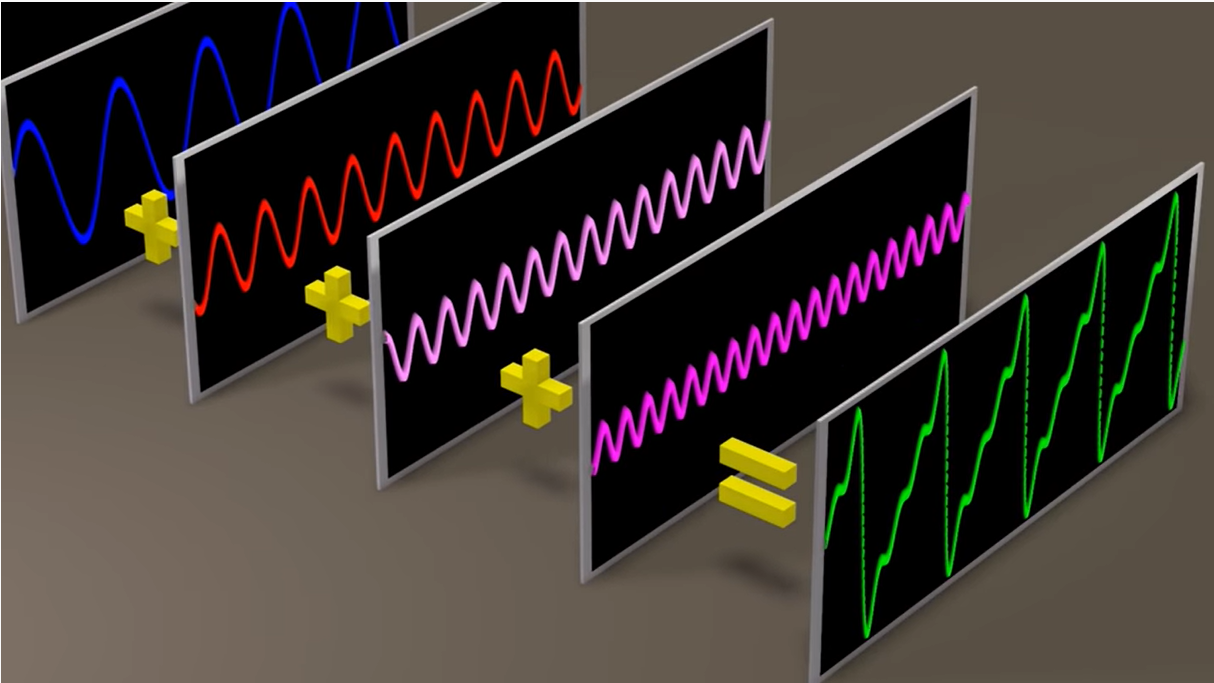
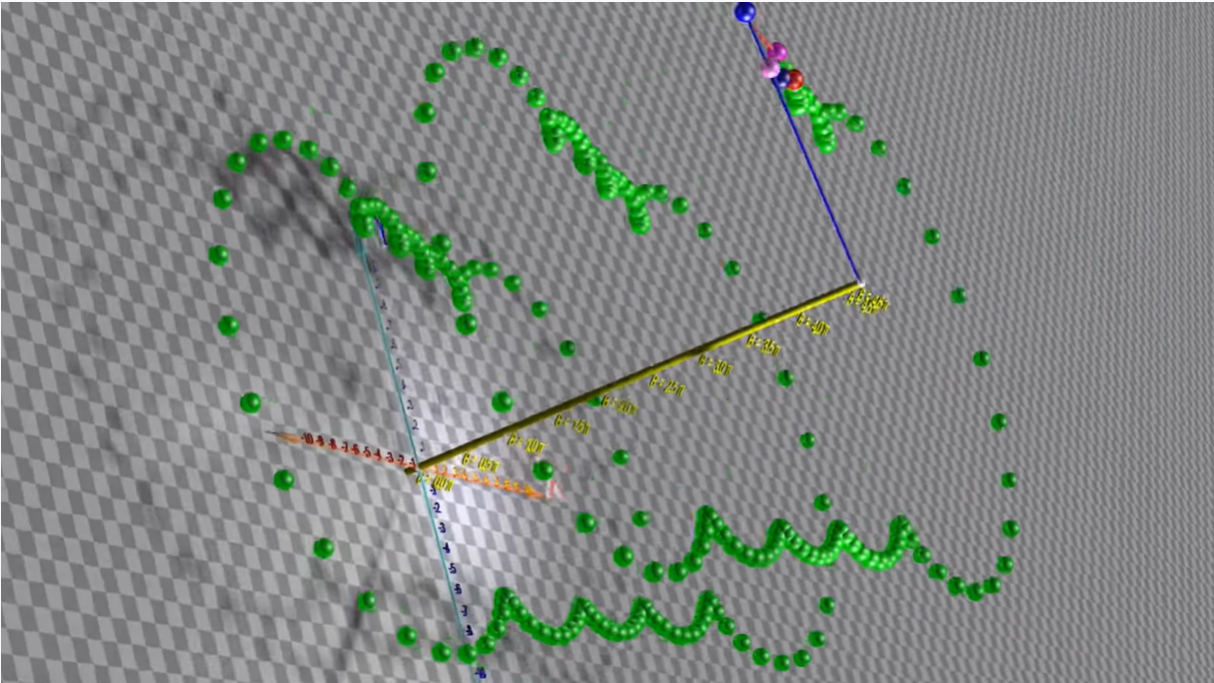
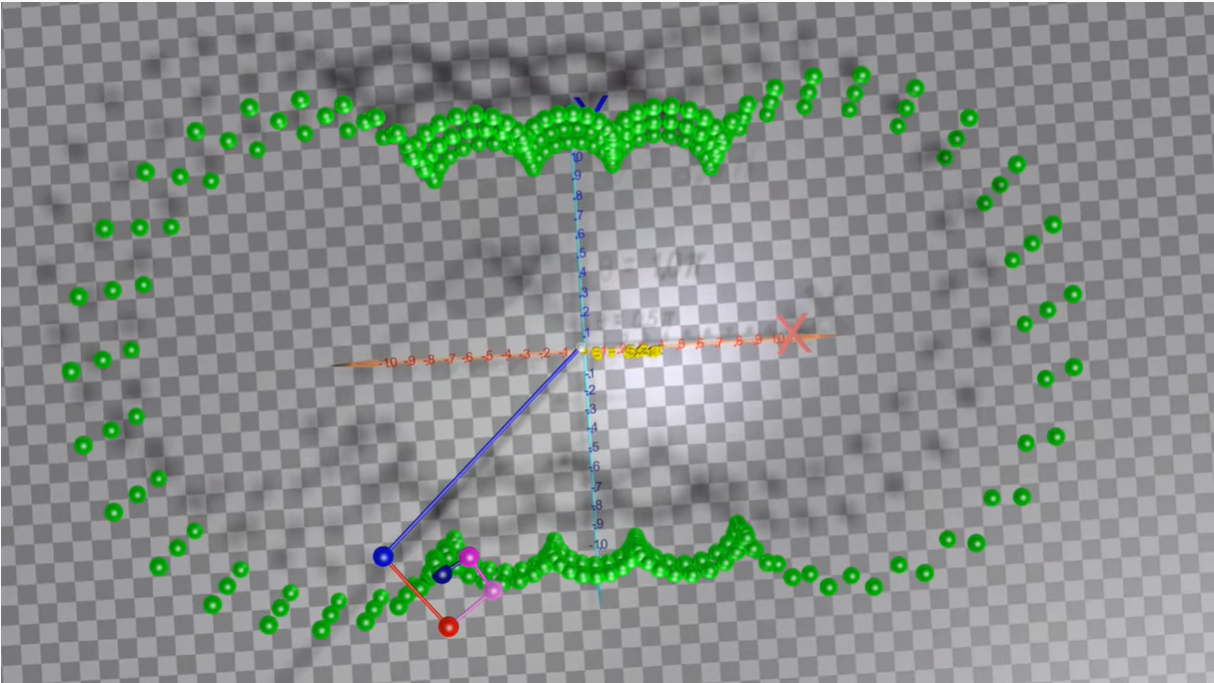
另一个五种相同相位、不同频率、不同振幅的正弦波叠加的例子：

这里的无数个正弦函数，其实就对应了傅里叶级数

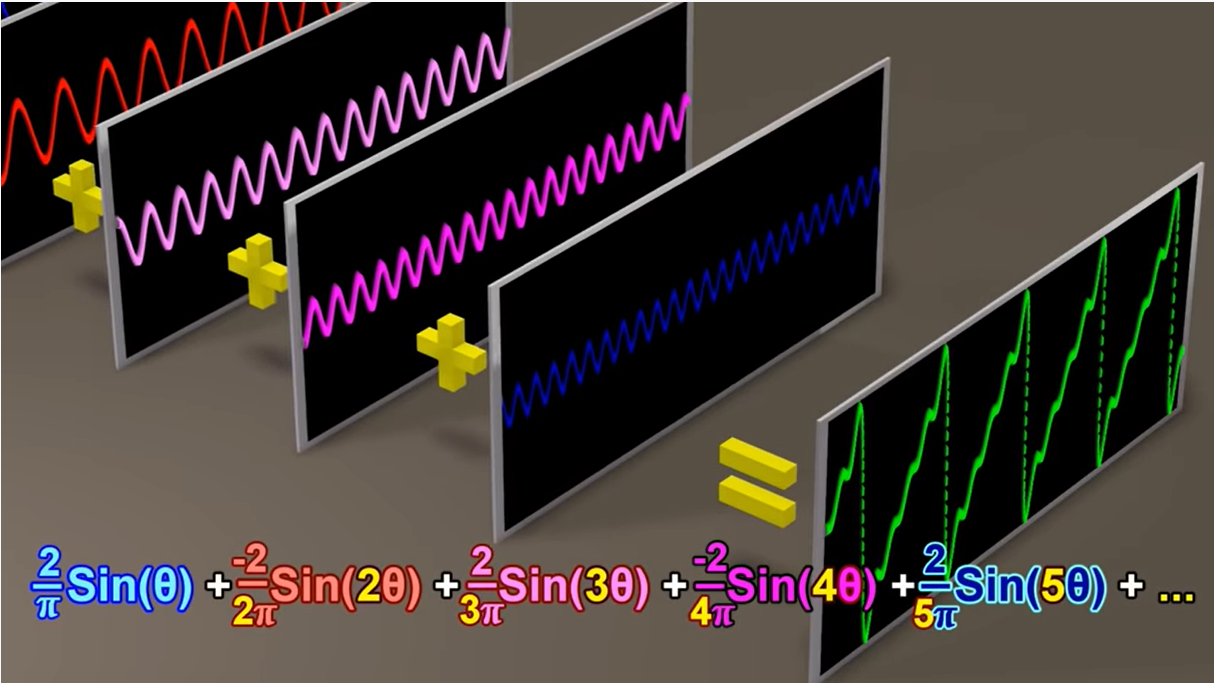
经证明，每一个波形和函数都可以通过不同的正弦波叠加在一起得到
这里的无数个正弦函数，其实就对应了傅里叶级数

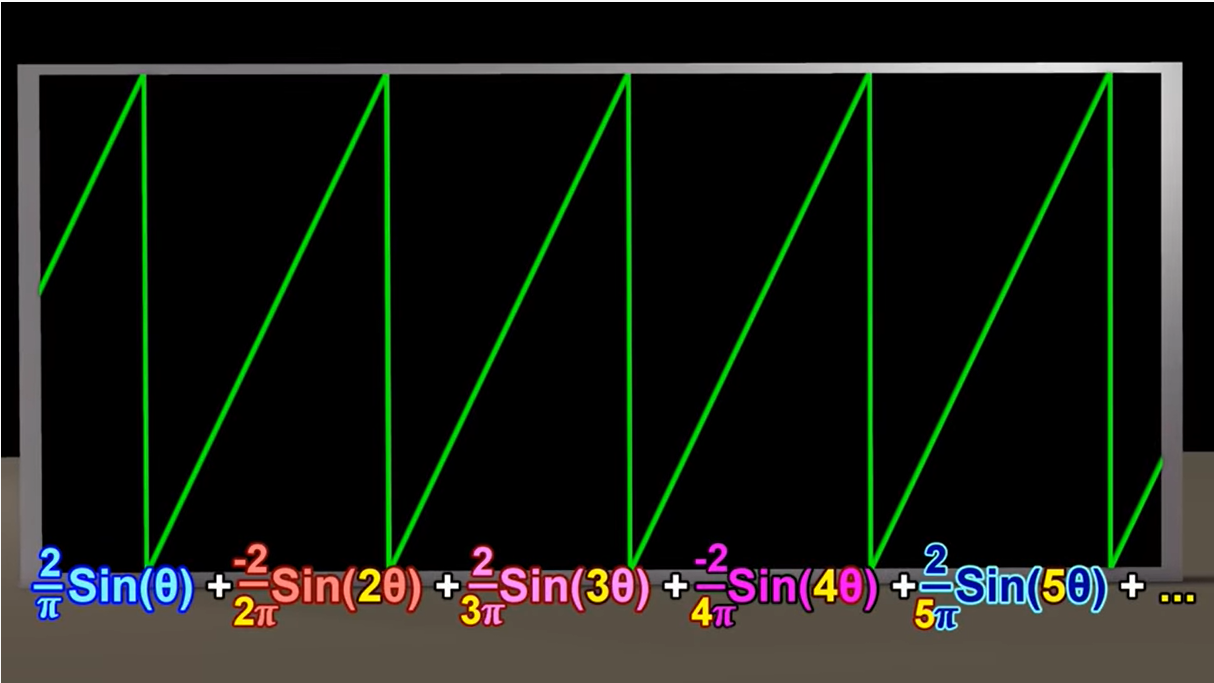
上面提到的两个例子中所有正弦波叠加会出现一个重复波形
这里再次列出上面两个示例

1.7 傅里叶级数和傅里叶变换区别

下图来自：傅里叶分析之掐死教程（完整版）更新于2014.06.06

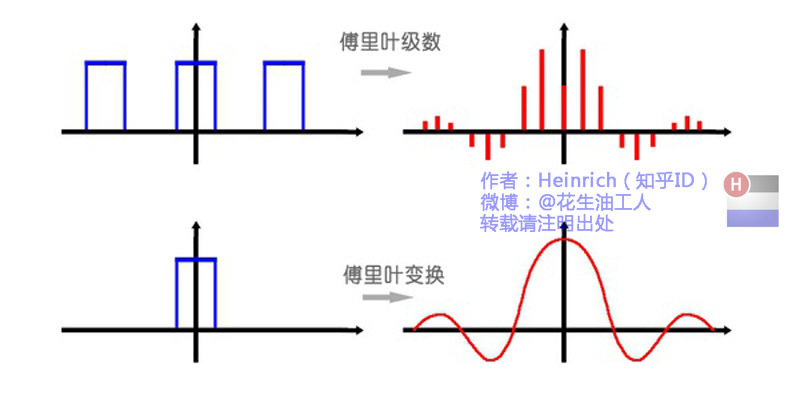
1.8 离散频谱

不重复的波形也可以通过正弦波叠加得到，但此时或许需要各种频率的正弦波，并且这些正弦波的振幅是无限小的

各种频率的正弦波

振幅无限小的正弦波

若将无限个振幅无限小的正弦波叠加之后，就可以得到可以观察和测量的波形了，类似于将无限个纸片叠起来，每张纸自身的体积几乎为0，但叠起来却可以得到一个可测量体积的物体

当我们把这个物体压实后，我们就可以测量它每个部分的密度了

同理，我们将无限个振幅无限小的正弦波叠加在一起就可以测量叠加后波的频率密度，这就是我们说的波形频谱（Frequency Spectrum）

下图来自：傅里叶分析之掐死教程（完整版）更新于2014.06.06
离散频谱

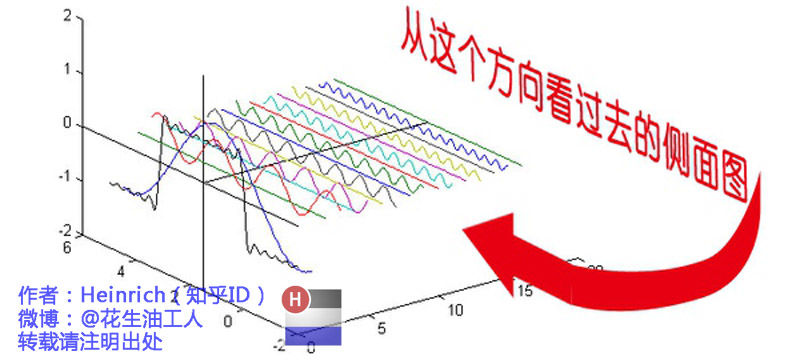
所有信号和波形都有一个频谱
当信号和波形与物质相互影响时，它们的频谱就会改变
通过理解频谱如何被改变，我们就可以理解信号和波形是如何被改变的

频域图像、时域图像

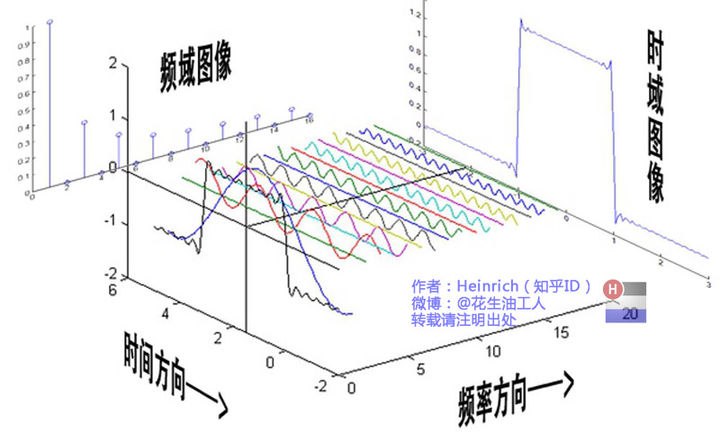
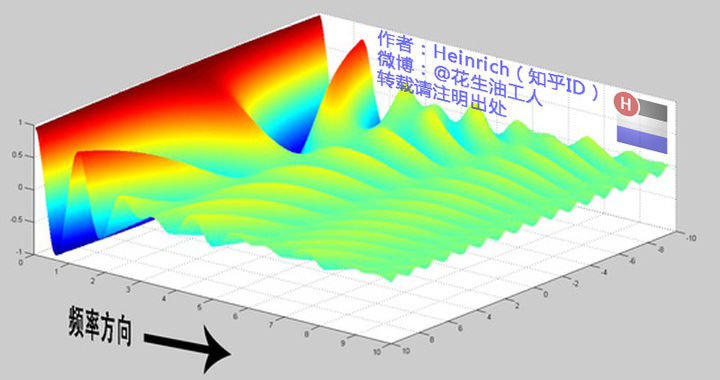
1.9 连续频谱

下图来自：傅里叶分析之掐死教程（完整版）更新于2014.06.06

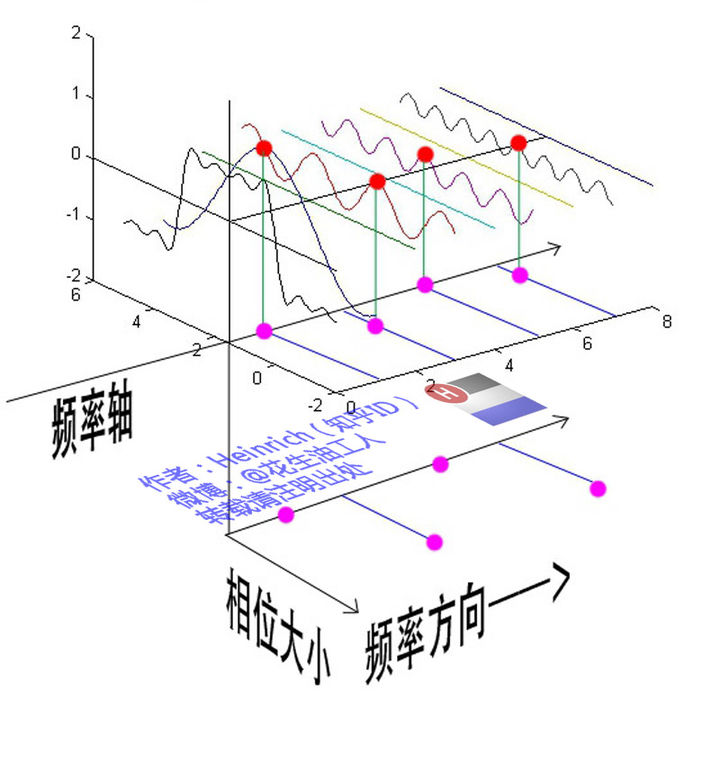
2.0 傅里叶级数的相位谱（离散）

下图来自：傅里叶分析之掐死教程（完整版）更新于2014.06.06

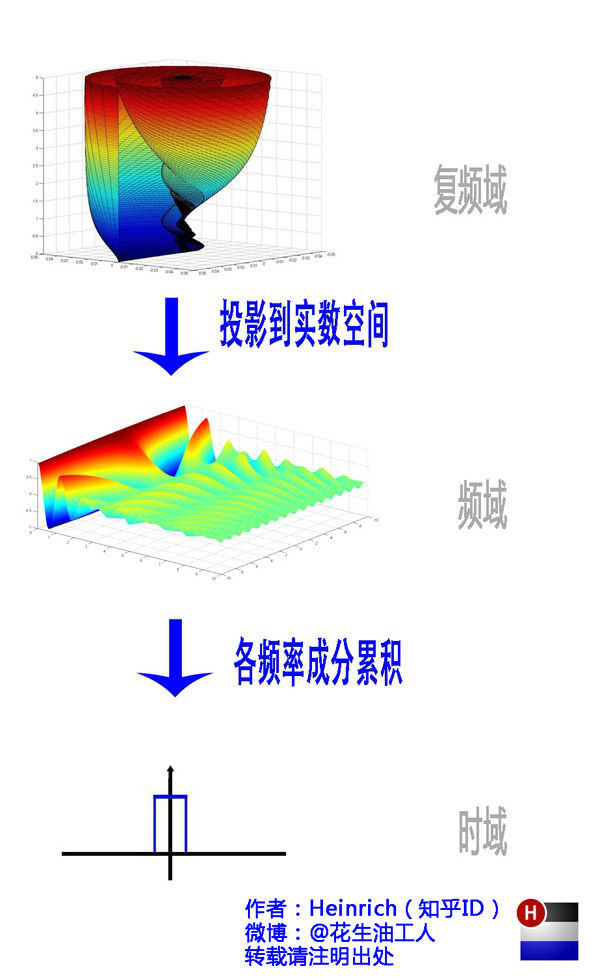
2.1 指数形式的傅里叶变换

下图来自：傅里叶分析之掐死教程（完整版）更新于2014.06.06

最后

以上就是甜蜜自行车为你收集整理的傅里叶级数、傅里叶变换、频谱1.傅里叶级数和傅里叶变换的全部内容，希望文章能够帮你解决傅里叶级数、傅里叶变换、频谱1.傅里叶级数和傅里叶变换所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。