概述
一、本期介绍函数的求解有两种
（1）已知x求y
（2）已知y求x
1.1已知x求y
回想我们上一期，讲了多项式求解的方法，也是已知x求y。想一下，多项式不也是函数的一种吗，所以本期求解的方法同样适用于多项式，只不过比多项式稍微麻烦了一点点点。同学在学完本期内容之后可以对比下上一期。
例1、求下列函数x=1,2,3,4,5对应y的值
对函数求解有两种方式：
1.1.1创建函数文件
这种方法的原理是：
（1）构造一个函数文件，表示我们定义了一个函数（比如fun(x)），以后我们就可以随便使用这个函数了（为什么不直接在matlab命令行构建？是因为每解一个x我们就要输入一次y的表达式，不太方便。）。
（2）然后我们在命令行输入x的值（可以是单个数，也可以是多个值），再调用该函数，就可以得到y的值了
下面具体求解过程：
首先创建一个函数文件，操作如下：
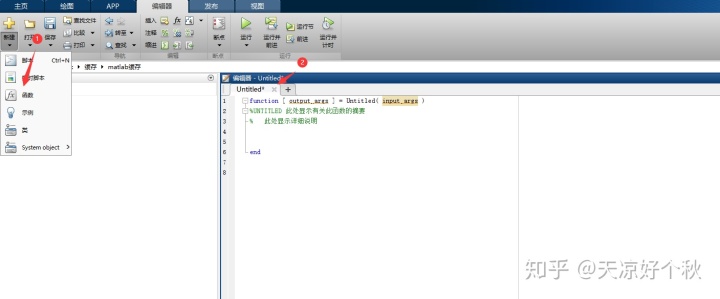
在该函数文件中输入如下：
function y = fun(x) %定义该函数的名称为fun()，在结果中显示返回值y
y = 4*x.^3+3*sin(x)+2; %输入y的表达式，注意要用.^，因为需要输入多个x
end %结束语句点击上面菜单栏的保存即可，然后可以看到左侧出现该函数文件名称。这时候我们可以直接调用
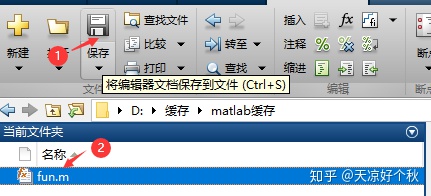
我们关闭函数文件界面，返回命令行窗口，输入：
x = [1,2,3,4,5];
fun(x)结果如下：
ans =
8.5244 36.7279 110.4234 255.7296 499.12321.1.2直接在命令行创建函数的方法（函数句柄）
这种方法和创建函数文件的方法其实是一样的，因为直接在命令行调用，所以比较方便。但是当编写较为复杂的函数文件时，再用这种方法就不够直观，而且容易出错。所以这种方法适用于简单、临时的函数。
具体操作如下：
fun = @(x) 4*x.^3+3*sin(x)+2;
x = [1,2,3,4,5];
y = fun(x)结果如下:
y =
8.5244 36.7279 110.4234 255.7296 499.1232可以看到，与构建函数文件得到的结果是一样的。
1.2已知y求x
要用到的函数:solve() ，用法如下
solve(y, x)：求解y=0时，自变量x的值。
既然我们要求解根，那么我们首先需要让x占一个空间，然后求解。
这里我们需要用到syms或sym(' ')来定义符号。操作如下：
syms x %将字符'x'定义为一个未知量
sym('x') %将字符'x'定义为一个未知量,输入麻烦，不常用好的，我们来实际应用一下
1.2.1 求解一元方程
例2、求解
syms x %定义自变量x，这里不定义y是因为在后面的求解过程中认为其是0，没有占用空间，定不定义都一样
y = x*sin(x)-x; %定义y，
solve(y,x) %求解y=0时，自变量x的值.也可以写成solve('x*sin(x)-x',x)结果如下：
ans =
0
pi/21.2.2 求解多元方程
solve(eq1, eq2, ..., x, y, ...)前面写方程，后面写未知数
例3、 求解二元一次方程
这里是两个未知数了，那么我们需要定义两个未知数，将等式右边的值移到等式左边
syms x y %空格隔开
eq1 = x-2*y-5;
eq2 = x+y-6;
A = solve(eq1,eq2,x,y) %前面写等式，后面写未知数。这里等式的顺序和未知数不影响结果。
%这里需要注意将solve结果赋值给A.因为solve函数只负责计算，并没有改变x,y是符号的性质
%matlab这样做的原因是为了区别谁是x谁是y结果如下：
A =
包含以下字段的 struct:
y: [1×1 sym]
x: [1×1 sym]那么我们如何去看x,y的值呢？请看下面
>> A.x
ans =
17/3
>> A.y
ans =
1/3好的，通过上面两道题的练习，我们应该知道含有多个未知数的解法了，而且也不限于多项式方程，更复杂的方程也可以求解。
二、函数的符号运算
求解未知数以字符表示的方程
与前面内容不同的是：变量是某些符号的表示，而不是具体的数值
例4、求方程的根
syms x a b
solve(a*x^2-b,x) %后面如果将自变量定义的是b,那么求解的就是b用x,a表示。如果没有定义，默认是x结果如下：
ans =
b^(1/2)/a^(1/2)
-b^(1/2)/a^(1/2)例5、当x=1,2,3,4,5时，将y用a,b表示
首先创建函数文件
function y = fun(x)
syms a b
y = a*x.^2-b;
end在命令行输入x，求y
x = [1,2,3,4,5];
fun(x)结果如下：
ans =
[ a - b, 4*a - b, 9*a - b, 16*a - b, 25*a - b]好的，通过这两道题的练习我们应该对定义符号变量有了充分的认识了。那么我们以后求解带有符号的方程都可以用这种方式。
总结
本节我们学习了函数的求解，包括构建函数及函数句柄@，并且还学习了含有符号变量的函数的运算。希望各位好好熟悉一下本节，非常重要，是以后复杂运算的基础。
操千曲而后晓声，观千剑而后识器
最后
以上就是要减肥香氛为你收集整理的matlab二元一次方程求解_2-函数的求解计算的全部内容，希望文章能够帮你解决matlab二元一次方程求解_2-函数的求解计算所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
![Matlab中怎么把一维数组逆序排列，如将a=[1,2,3,4,5],转成b=[5,4,3,2,1]](/uploads/reation/bcimg6.png)
发表评论 取消回复