MATLAB数据及其运算笔记
- 2.1 MATLAB数值数据
- 2.1.1 数值数据类型的分类
- 1.整型
- 2.浮点型
- 3.复型
- 2.1.2 数据的输出格式
- 2.2 MATLAB矩阵的表示
- 2.2.1 矩阵的建立
- 2.2.2 冒号表达式
- 2.2.3 矩阵的引用
- 1.矩阵元素的引用方式MATLAB通过下标引用矩阵的元素
- 2.利用冒号表达式获得子矩阵
- 3.利用空矩阵删除矩阵的元素
- 4.改变矩阵的形状
- 2.3 变量及其操作
- 2.3.1 变量与赋值语句
- 1.变量命名
- 2.赋值语句
- 2.3.2预定义变量
- 2.3.3 变量的管理
- 1.内存变量的删除与修改
- 2.4 MATLAB常用内部函数
- 2.4.1 常用数学函数
- 2.4.2 矩阵的超越函数
- 1.矩阵平方根
- 2.矩阵对数
- 3.矩阵指数
- 4.普通矩阵函数
- 2.5 MATLAB运算
- 2.5.1 算术运算
- 1.基本算术运算
- 2.点运算
- 2.5.2 关系运算
- 2.5.3 逻辑运算
- 2.6 字符串
- 2.6.1 字符串的表示
- 2.6.2 字符串的操作
- 2.7 结构数据和单元数据
- 2.7.1 结构数据
- 2.7.2 单元数据
声明:
笔记是学习慕课网《科学计算与MATLAB语言》课程和刘卫国主编的《MATLAB程序设计与应用(第3版)》后的个人总结,方便自己以后巩固和复习!
2.1 MATLAB数值数据
2.1.1 数值数据类型的分类
1.整型
整型数据是不带小数的数,分为有带符号整数和无符号整数。
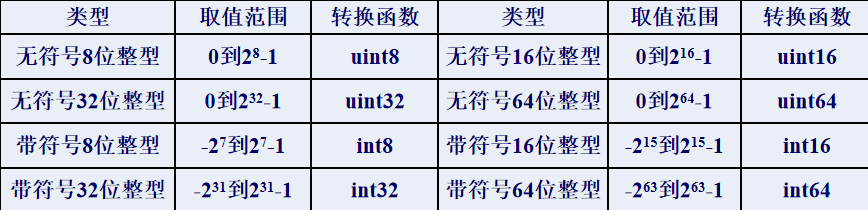
2.浮点型
浮点型数据有单精度(single)和双精度(double)之分,单精度型实数在内存中占用4个字节,双精度型实数在内存中占用8个字节,双精度型的数据精度更高。
在Matlab中,数据默认为双精度型。
single函数 可以将其他类型的数据转换为单精度型;利用class可以得到参数的数据类型。
double函数 可以将其他类型的数据转换为双精度型。

3.复型
复型数据包括实部和虚部两个部分,实部和虚部默认为双精度型。
在MATLAB中,虚数单位用i或j表示。
例如,6+5i与6+5j表示的是同一个复数,也可以写成6+5i或6+5j,这里将i或j看作一个运算量参与表达式的运算。
2.1.2 数据的输出格式
MATLAB用十进制数表示一个常数,具体可采用日常记数法和科学记数法两种表示方法。
format命令的格式为:
format 格式符
其中,格式符决定数据的输出格式,各种格式符及其含义如表所示。
| 格式符 | 含义 |
|---|---|
| short | 输出小数点后4位,最多不超过7位有效数字。对于大于1000的实数,用5位有效数字的科学记数形式输出 |
| long | 15位有效数字形式输出 |
| short e | 5位有效数字的科学记数形式输出 |
| long e | 15位有效数字的科学记数形式输出 |
| short g | 从short和short e中自动选择最佳输出方式 |
| long g | 从long和long e中自动选择最佳输出方式 |
| rat | 近似有理数表示 |
| hex | 十六进制表示 |
| + | 正数、负数、零分别用+、-、空格表示 |
| bank | 银行格式,用元、角、分表示 |
| compact | 输出变量之间没有空行 |
| loose | 输出变量之间有空行 |
注意:format命令只影响数据输出格式,而不影响数据的计算和存储。
2.2 MATLAB矩阵的表示
2.2.1 矩阵的建立
1.直接输入法:
最简单的建立矩阵的方法是从键盘直接输入矩阵的元素。
具体方法如下:将矩阵的元素用方括号括起来,按矩阵行的顺序输入各元素,同一行的各元素之间用空格或逗号分隔,不同行的元素之间用分号分隔。

2.2.2 冒号表达式
冒号表达式可以产生一个行向量,
一般格式是:
e1:e2:e3
其中e1为初始值,e2为步长,e3为终止值。

初始值:4 步长:3 终止值:12。
在MATLAB中,还可以用linspace函数产生行向量。
其调用格式为:
linspace(a,b,n)
其中a和b是生成向量的第一个和最后一个元素,n是元素总数。
显然,linspace(a,b,n)与a:(b-a)/(n-1):b等价
2.2.3 矩阵的引用
1.矩阵元素的引用方式MATLAB通过下标引用矩阵的元素
例如:A(3,2)=200
也可以采用矩阵元素的序号来引用矩阵元素。矩阵元素的序号就是相应元素在内存中的排列顺序。
在MATLAB中,矩阵元素按列存储,先第一列,再第二列,依次类推。
显然,序号(Index)与下标(Subscript )是一一对应的,以m×n矩阵A为例,矩阵元素A(i,j)的序号为(j-1)*m+i。其相互转换关系也可利用sub2ind和ind2sub函数求得。

2.利用冒号表达式获得子矩阵
① A(:,j)表示取A矩阵的第j列全部元素;A(i,:)表示A矩阵第i行的全部元素;A(i,j)表示取A矩阵第i行、第j列的元素。
② A(i:i+m,:)表示取A矩阵第i~i+m行的全部元素;A(:,k:k+m)表示取A矩阵第k~k+m列的全部元素,A(i:i+m,k:k+m)表示取A矩阵第i~i+m行内,并在第k~k+m列中的所有元素。 ③A(:)将矩阵A每一列元素堆叠起来,成为一个列向量,而这也是MATLAB变量的内部储存方式。
3.利用空矩阵删除矩阵的元素
在MATLAB中,定义[]为空矩阵。给变量X赋空矩阵的语句为
X=[]
注意,X=[]与clear X不同,clear是将X从工作空间中删除,而空矩阵则存在于工作空间中,只是维数为0。
4.改变矩阵的形状
reshape(A,m,n)函数在矩阵总元素保持不变的前提下,将矩阵A重新排成m×n的二维矩阵。
例如:
x=[23,45,65,34,65,34,98,45,78,65,43,76
y=reshape(x,3,4
y =
23 34 98 65
45 65 45 43
65 34 78 76
注意:
reshape函数只是改变原矩阵的行数和列数,即改变其逻辑结构,但并不改变原矩阵元素个数及其存储顺序。
A(:)将矩阵A的每一列元素堆叠起来,成为一个列向量,从而改变了矩阵的形状。
2.3 变量及其操作
2.3.1 变量与赋值语句
1.变量命名
在MATLAB 7.0中,**变量名是以字母开头,后接字母、数字或下划线的字符序列,最多63个字符。**在MATLAB中,变量名区分字母的大小写。
2.赋值语句
(1) 变量=表达式
(2) 表达式
其中表达式是用运算符将有关运算量连接起来的式子,其结果是一个矩阵。
例如:计算表达式的值,并显示计算结果
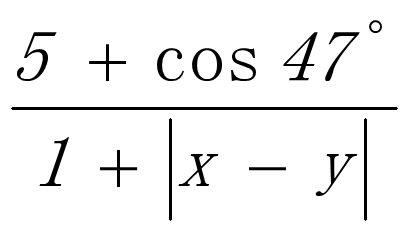
在MATLAB命令窗口输入命令:
>> x=sqrt(7)-2i;
y=exp(pi/2);
z=(5+cos(47*pi/180))/(1+abs(x-y))

2.3.2预定义变量
在MATLAB工作空间中,还驻留几个由系统本身定义的变量。例如,用pi表示圆周率π的近似值,用i,j表示虚数单位。
预定义变量有特定的含义,在使用时,应尽量避免对这些变量重新赋值。
2.3.3 变量的管理
1.内存变量的删除与修改
MATLAB工作区窗口专门用于内存变量的管理。在工作区窗口中可以显示所有内存变量的属性。
who和whos这两个命令用于显示在MATLAB工作空间中已经驻留的变量名清单。
who命令只显示出驻留变量的名称;
whos在给出变量名的同时,还给出它们的大小、所占字节数及数据类型等信息。

clear命令用于删除MATLAB工作空间中的变量。
2.内存变量文件利用MAT文件可以把当前MATLAB工作空间中的一些有用变量长久地保留下来,扩展名是.mat。MAT文件的生成和装入由save和load命令来完成。常用格式为:
save 文件名 [变量名表] [-append] [-ascii]
load 文件名 [变量名表] [-ascii]
其中,文件名可以带路径,但不需带扩展名.mat,命令隐含一定对.mat文件进行操作。变量名表中的变量个数不限,只要内存或文件中存在即可,变量名之间以空格分隔。当变量名表省略时,保存或装入全部变量。-ascii选项使文件以ASCII格式处理,省略该选项时文件将以二进制格式处理。save命令中的-append选项控制将变量追加到MAT文件中。
2.4 MATLAB常用内部函数
2.4.1 常用数学函数
MATLAB提供了许多数学函数,函数的自变量规定为矩阵变量,运算法则是将函数逐项作用于矩阵的元素上,因而运算的结果是一个与自变量同维数的矩阵。
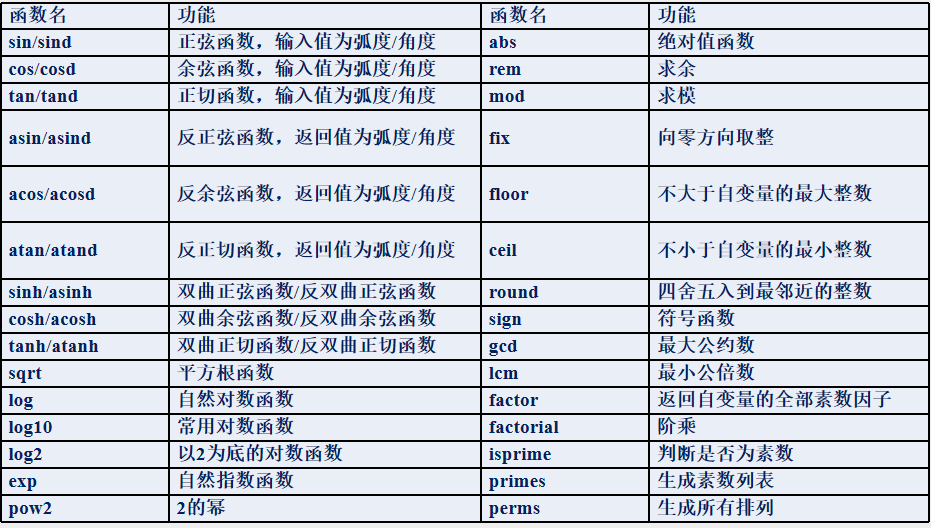
2.4.2 矩阵的超越函数
MATLAB还提供了一些直接作用于矩阵的超越函数,这些函数名都在上述内部函数名之后缀以m,并规定输入参数A必须是方阵。
1.矩阵平方根
sqrtm(A)计算矩阵A的平方根。

2.矩阵对数
logm(A)计算矩阵A的自然对数。此函数输入参数的条件与输出结果间的关系和函数sqrtm(A)完全一样。

3.矩阵指数
expm(A)的功能都是求矩阵指数eA。例如,对上面计算所得到的A的自然对数b.
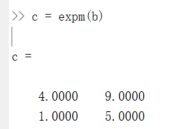
4.普通矩阵函数
funm(A,@fun)对方阵A计算由fun定义的函数的矩阵函数值。例如,当fun取exp时,funm(A,@exp)可以计算矩阵A的指数,与expm(A)的计算结果一样。

2.5 MATLAB运算
2.5.1 算术运算
1.基本算术运算
MATLAB的基本算术运算有:+(加)、-(减)、*(乘)、/(右除)、(左除)、^(乘方)。
注意,运算是在矩阵意义下进行的,单个数据的算术运算只是一种特例。
(1) 矩阵加减运算
假定有两个矩阵A和B,则可以由A+B和A-B实现矩阵的加减运算。运算规则是:若A和B矩阵的维数相同,则可以执行矩阵的加减运算,A和B矩阵的相应元素相加减。如果A与B的维数不相同,则MATLAB将给出错误信息,提示用户两个矩阵的维数不匹配。
(2) 矩阵乘法
假定有两个矩阵A和B,若A为m×n矩阵,B为n×p矩阵,则C=A*B为m×p矩阵。
(3) 矩阵除法
在MATLAB中,有两种矩阵除法运算:和/,分别表示左除和右除。
如果A矩阵是非奇异方阵,则AB和B/A运算可以实现。
AB等效于A的逆左乘B矩阵,也就是inv(A) *B,
而B/A等效于A矩阵的逆右乘B矩阵,也就是B*inv(A)。

(4) 矩阵的乘方
一个矩阵的乘方运算可以表示成A^x,要求A为方阵,x为标量。
A^2 = A*A

2.点运算
在MATLAB中,有一种特殊的运算,因为其运算符是在有关算术运算符前面加点,所以叫点运算。点运算符有.*、./、.和.^。两矩阵进行点运算是指它们的对应元素进行相关运算,要求两矩阵的维参数相同。
2.5.2 关系运算
MATLAB提供了6种关系运算符:
< (小于)、<=(小于或等于)、>(大于)、>=(大于或等于)、==(等于)、~=(不等于)。
它们的含义不难理解,但要注意其书写方法与数学中的不等式符号不尽相同。
关系运算符的运算法则为:
(1) 当两个比较量是标量时,直接比较两数的大小。若关系成立,关系表达式结果为1,否则为0。
(2) 当参与比较的量是两个维数相同的矩阵时,比较是对两矩阵相同位置的元素按标量关系运算规则逐个进行,并给出元素比较结果。最终的关系运算的结果是一个维数与原矩阵相同的矩阵,它的元素由0或1组成。
(3) 当参与比较的一个是标量,而另一个是矩阵时,则把标量与矩阵的每一个元素按标量关系运算规则逐个比较,并给出元素比较结果。最终的关系运算的结果是一个维数与原矩阵相同的矩阵,它的元素由0或1组成。
例如:
建立5阶方阵A,判断A的元素是否能被3整除
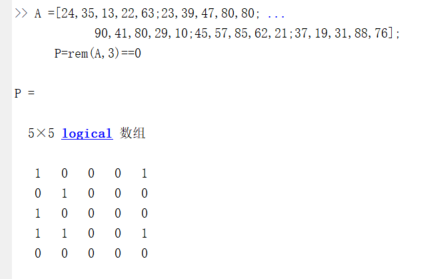
其中,rem(A,3)是矩阵A的每个元素除以3的余数矩阵。此时,0被扩展为与A同维数的零矩阵,P是进行等于(==)比较的结果矩阵。
2.5.3 逻辑运算
MATLAB提供了3种逻辑运算符:&(与)、|(或)和~(非)。
逻辑运算的运算法则为:
(1) 在逻辑运算中,确认非零元素为真,用1表示,零元素为假,用0表示。
(2) 设参与逻辑运算的是两个标量a和b,
那么,a&b a,b全为非零时,运算结果为1,否则为0。
a|b a,b中只要有一个非零,运算结果为1。
~a 当a是零时,运算结果为1;当a非零时,运算结果为0。
(3) 若参与逻辑运算的是两个同维矩阵,那么运算将对矩阵相同位置上的元素按标量规则逐个进行。最终运算结果是一个与原矩阵同维的矩阵,其元素由1或0组成。
(4) 若参与逻辑运算的一个是标量,一个是矩阵,那么运算将在标量与矩阵中的每个元素之间按标量规则逐个进行。最终运算结果是一个与矩阵同维的矩阵,其元素由1或0组成。
(5) 逻辑非是单目运算符,也服从矩阵运算规则。
(6) 在算术、关系、逻辑运算中,算术运算优先级最高,逻辑运算优先级最低。
2.6 字符串
2.6.1 字符串的表示
在MATLAB中,字符串是用单引号括起来的字符序列。例如:
xm='Central South University'
例:建立一个字符串向量,然后对该向量做如下处理:
(1) 取第1~5个字符组成的子字符串。
(2) 将字符串倒过来重新排列。
(3) 将字符串中的小写字母变成相应的大写字母,其余字符不变。
(4) 统计字符串中小写字母的个数。
ch='ABc123d4e56Fg9';
subch=ch(1:5) %取子字符串
revch=ch(end:-1:1) %将字符串倒排
k=find(ch>='a'&ch<='z'); %找小写字母的位置
ch(k)=ch(k)-('a'-'A'); %将小写字母变成相应的大写字母
char(ch)
length(k) %统计小写字母的个数
注意是英文下的单撇号;‘ABc123d4e56Fg9’,不是‘ABc123d4e56Fg9’
2.6.2 字符串的操作
1.字符串的执行
与字符串有关的一个重要函数是eval,它的作用是把字符串的内容作为对应的MATLAB命令来执行,其调用格式为:
eval(s)
其中s为字符串。例如:
>> t=pi;
m='[t,sin(t),cos(t)]';
y=eval(m)
y =
3.1416 0.0000 -1.0000
2.字符串与数值之间的转换
字符串是以ASCII码形式存储的,abs和double函数都可以用来获取字符串矩阵所对应的ASCII码数值矩阵。
3.字符串的连接
在MATLAB中,要将两个字符串连接在一起,有两种常见方法:一是用字符串向量,二是用strcat函数。
4.字符串的比较
字符串的比较有两种方法:利用关系运算符或字符串比较函数。
当两个字符串拥有相同的长度时,可以利用关系运算符对字符串进行比较,比较的规则是按ASCII值大小逐个字符进行比较,比较的结果是一个数值向量,其元素为对应字符比较的结果。例如:
>> 'www0'>='W123'
ans =
1 1 1 0
字符串比较函数用于判断字符串是否相等,有4种比较方式,函数如下:
① strcmp(s1,s2):用来比较字符串s1和s2是否相等,如果相等,返回1,否则返回0。
② strncmp(s1,s2,n):用来比较前n个字符是否相等,如果相等,返回1,否则返回0。
③ strcmpi(s1,s2):在忽略字母大小写前提下,比较字符串s1和s2是否相等,如果相等,返回1,否则返回0。
④ strncmpi(s1,s2,n):在忽略字符串大小写前提下,比较前n个字符是否相等,如果相等,返回1,否则返回0。
2.7 结构数据和单元数据
2.7.1 结构数据
1.结构矩阵的建立与引用
建立一个结构矩阵可采用给结构成员赋值的办法。
具体格式为:
结构矩阵名.成员名=表达式
其中表达式应理解为矩阵表达式。
2.结构成员的修改
可以根据需要增加或删除结构的成员。
例如要给结构矩阵a增加一个成员x4,可给a中任意一个元素增加成员x4:
a(1).x4=‘410075’;
但其他成员均为空矩阵,可以使用赋值语句给它赋确定的值。
要删除结构的成员,则可以使用rmfield函数来完成。
例如,删除成员x4:
a=rmfield(a,‘x4’);
2.7.2 单元数据
建立单元矩阵和一般矩阵相似,只是矩阵元素用大括号括起来。
可以用带有大括号下标的形式引用单元矩阵元素。例如b{3,3}。单元矩阵的元素可以是结构或单元数据。
可以使用celldisp函数来显示整个单元矩阵,如celldisp(b)。
最后
以上就是愤怒小土豆最近收集整理的关于MATLAB学习笔记(二)——数据及其运算的全部内容,更多相关MATLAB学习笔记(二)——数据及其运算内容请搜索靠谱客的其他文章。
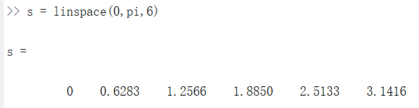








发表评论 取消回复