1. 首页
  2. 文章中心
  3. 系统辨识

matlab使用相关分析法和hankel矩阵法进行系统辨识

66 阅读 0 评论
我是靠谱客的博主 愉快魔镜，最近开发中收集的这篇文章主要介绍matlab使用相关分析法和hankel矩阵法进行系统辨识，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

待辨识模型：
%H = 180.60 / ( 48.96s^2 + 14.00s + 1.0 )
H = tf( [180.60],[ 48.96 14 1.0 ] ) ;
b = [ 180.60 ] ;
a = [ 48.96 14 1.0 ];
待辨识模型转化为离散模型,可以适用脉冲响应不变法，也可以使用双线性变换法方法，采样时间为1S
采样时间的标准，采样时间选择标准如下，fmax为系统截止频率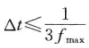在这里插入图片描述
[bz,az] = impinvar(b,a,1 );%使用脉冲响应不变法将S域转到Z域
[bz1,az1] = bilinear(b,a,1) %使用双线性变换的方法，将S域转到Z域
通过系统的阶跃响应的图形，观察系统的过渡时间
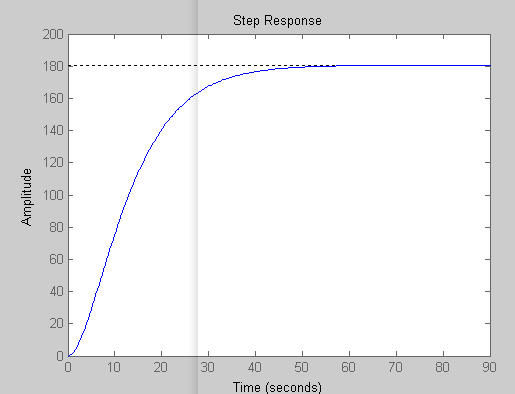
在这里插入图片描述
取过渡时间为50s
选择M序列的寄存器个数
n = 6 ;
N = 2^n - 1 ;
即M序列的一个周期为63个点
%生成M序列用于辨识系统的模型
n = 6 ;%M序列取4个移位寄存器
N = 2^n - 1 ; %总的M序列的点数
%Tuse * （ Np-1）> T95 ( 在范围(1.2 ~ 1.5 )T95 )
a = 1;
delta = T0 ;
%M序列出来的值会跟初值有关，所以出来的值根据初值不同有多种情况
A = zeros( n , 1 ) ; %A数组
X = zeros( n , 1 ) ; %X数组
XOR = zeros( n , 1 ) ; %XOR数组
A(1) = 1 ;
A(2) = 1 ;
A(3) = 1 ;
A(4) = 1 ;
A(5) = 1 ;
A(6) = 0 ;
XOR( 6 ) = 1 ;
XOR( 5 ) = 1 ;
r = 4 ; %周期数
for i = 1 : rN
X(1) = xor( A(6), A(5) ) ;
for i1 = 2 : n
X( i1 ) = A( i1 -1 ) ;
end
OUT( i ) = A(n);
t( i ) = deltai ;
if OUT( i ) > 0.5
u( i ) = a ;
else u( i ) = -a;
end
for j = 1 : n
A( j ) = X( j ) ;
end
end
通过生成的M序列，输入系统的离散模型中，生成离散模型的输出数据Y
%Ny 表示方程的阶次，进行输入输出数组的填充
Ny = 2 ;
Y = zeros( r * N + Ny , 1 );
X = zeros( r * N + Ny , 1 );
YPulse = zeros( r * N + Ny , 1 );
XPulse = zeros( r * N + Ny , 1 );
XPulse(3) = a ;
% YPulse1 = zeros( r * N + Ny , 1 );
% XPulse1 = zeros( r * N + Ny , 1 );
% XPulse1(3) = 1/(T0) ;
for i = 1 : r * N
%X( i + Ny ) = u( i ) ;
X( i + Ny ) = u( i ) ;
end
for i = 1 : r * N
Y( i + Ny ) = 0.8033 * X( i + Ny ) + …
1.6065 X( i + Ny - 1 ) + …
0.8033 * X( i + Ny - 2 ) + …
1.7332 * Y( i + Ny - 1 ) - …
0.7510 * Y( i + Ny - 2 );
end
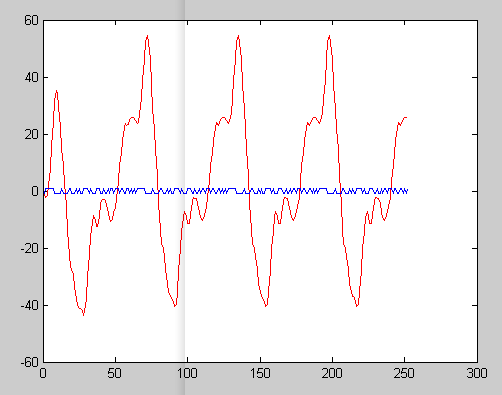
在这里插入图片描述
接下来采用相关分析法，仅仅根据输入数据和输出数据，得到系统的脉冲响应曲线
Y1 = Y( Ny + ( r - 1 ) * N + 1 : r * N + Ny ) ;
X1 = X( Ny + ( r - 1 ) * N + 1 : r * N + Ny ) ;
YSum = 0 ;
for i = 1 : N
YSum = YSum + Y1( i ) ;
end
YAvr = YSum / N ;
Y1 = Y1 - YAvr ;%减去直流分量
Rmz = zeros( N , 1) ;
%计算互相关矩阵，输入与输出的互相关矩阵，进行卷积
for i = 1 : N
Rmz( i )= 0 ;
sum = 0 ;
for j = 1 : N
if( j >= i )
sum = sum + X1( j - i + 1 ) * Y1( j ) ;
else
sum = sum + X1( N - ( i - j ) + 1 )*Y1( j ) ;
end
end
Rmz( i ) = sum / N ;
end
c = -Rmz( N ) ;
gK = ( N * ( Rmz + c ))/( ( N + 1 ) * ( a ^ 2 ) )
gY = impz( bz1,az1 ,50,1) ;
figure(1)
plot( 1 : N , gK , ‘r’)
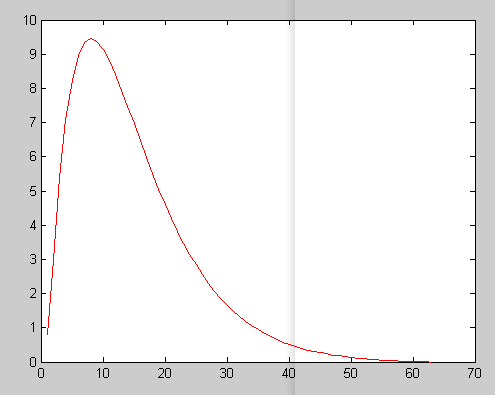
在这里插入图片描述
接下来使用Hankel矩阵的方法，获取系统的模型的参数
%通过Hankel矩阵进行模型的辨识
Nsys = 2 ;%待辨识的系统的系统的阶次
Gsys1 = zeros( Nsys , Nsys ) ;
Asys1 = zeros( Nsys , 1 ) ;
Gsys2 = zeros( Nsys , 1 ) ;
%注意Gsys是从1开始的
for i = 1 : Nsys
for j = 1 : Nsys
Gsys1( i , j ) = gK( i + j ) ;
end
Gsys2( i ) = -gK( Nsys + i + 1 ) ;
end
Asys1 = inv( Gsys1 ) * Gsys2
Bsys1 = zeros( Nsys + 1 , 1 ) ;
Gsys2 = [ gK( 1 : Nsys + 1 ) ] ;
Asys2 = eye(Nsys + 1 ) ;
for i = 2 : Nsys + 1
Asys2( i , : ) = [ Asys1( Nsys - ( i - 2 ):Nsys )’ , Asys2( i , i : Nsys + 1 ) ] ;
end
Asys2;
Gsys2;
Bsys1 = Asys2 * Gsys2 ;
Aresult = [ 1 , flip( Asys1’ ) ];
Bsys1
Asys1
GY1 = impz( Bsys1 ,[ 1 , flip( Asys1’ ) ] , 50 , 1);
figure(2);
% plot( 1 : size(gY) , gY , ‘r’ , 1 : size(YPulse) , YPulse , ‘b’, 1:size(YPulse1),YPulse1,‘g’);
plot( 1 : N , gK , ‘r’ , 1 : size(GY1) , GY1 , ‘b’);
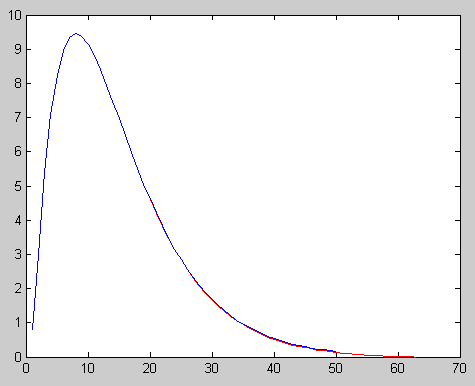
在这里插入图片描述
拟合出的曲线与使用相关分析法分析出来的曲线能很好的重合
辨识出来的模型参数，asys1为传递函数的分母的参数
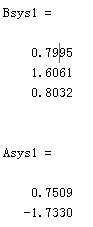
在这里插入图片描述
待辨识的系统的离散模型的参数
在这里插入图片描述
附上代码段：

%H = 180.60 / ( 48.96s^2 + 14.00s + 1.0 )
H = tf( [180.60],[ 48.96 14 1.0 ] ) ; 
figure(3) ; 
step( H ) ; 
T95 = 35 ; %上升时间是35S
T0 = 1; %采样时间取上升时间的( 1/5 ~ 1/15 ) ;
%如果采样时间取整形，则出来的阶跃响应的波形会存在误差
%改为使用浮点形，则可以减小误差
b = [ 180.60 ] ; 
a = [ 48.96 14 1.0 ];
f = 0 : 0.01 : 2 ;
w = 2*pi*f ;
% figure(6)
% freqs(b,a,w)
[bz,az] = impinvar(b,a,1 );%使用脉冲响应不变法将S域转到Z域
[bz1,az1] = bilinear(b,a,1) %使用双线性变换的方法，将S域转到Z域
% [bz2,az2] = bilinear(b,a,1/T0);
%使用脉冲响应不变法得到的模型
G = tf( bz ,az , T0 ) ;
%figure(3) ; 
%step( G ) ; 
%使用双线性变换后得到的模型
% G1 = tf( bz1 , az1 , 1 ) ;
% G2 = tf( bz2 , az2 , T0 ) ;
% figure(3) ; 
% step(G1) ;
% figure(4) ; 
% step(G2) ; 
% figure(5);
% step(G)
%生成M序列用于辨识系统的模型
n = 6 ;%M序列取4个移位寄存器
N = 2^n - 1 ; %总的M序列的点数
%Tuse * （ Np-1）> T95 ( 在范围(1.2 ~ 1.5 )*T95 )
a = 1; 
delta = T0 ; 
%M序列出来的值会跟初值有关，所以出来的值根据初值不同有多种情况
A = zeros( n , 1 ) ; %A数组
X = zeros( n , 1 ) ; %X数组
XOR = zeros( n , 1 ) ; %XOR数组
A(1) = 1 ; 
A(2) = 1 ; 
A(3) = 1 ; 
A(4) = 1 ;
A(5) = 1 ; 
A(6) = 0 ; 
XOR( 6 ) = 1 ;
XOR( 5 ) = 1 ; 
r = 4 ; %周期数
for i = 1 : r*N 
        X(1) = xor( A(6), A(5) ) ;
    for i1 = 2 : n
        X( i1 ) = A( i1 -1 ) ;
    end
    OUT( i ) = A(n); 
    t( i ) = delta*i ; 
    if OUT( i ) > 0.5 
        u( i ) = a ; 
    else u( i ) = -a; 
    end 
    for j = 1 : n 
        A( j ) = X( j ) ; 
    end
end
%Ny 表示方程的阶次，进行输入输出数组的填充
Ny = 2 ; 
Y = zeros( r * N + Ny , 1 );
X = zeros( r * N + Ny , 1 );
YPulse = zeros(  r * N + Ny , 1 );
XPulse = zeros(  r * N + Ny , 1 );
XPulse(3) = a ;
% YPulse1 = zeros(  r * N + Ny , 1 );
% XPulse1 = zeros(  r * N + Ny , 1 );
% XPulse1(3) = 1/(T0) ;
for i = 1 : r * N 
    %X( i + Ny ) = u( i ) ;
    X( i + Ny ) = u( i ) ;
end
%进行差分方程的计算
% for i = 1 : r * N 
%     Y( i + Ny ) = 3.688 * X( i + Ny )     + ...
%                   7.376 * X( i + Ny - 1 ) + ...
%                   3.688 * X( i + Ny - 2 ) + ...
%                   1.488 * Y( i + Ny - 1 ) - ...
%                   0.5099 * Y( i + Ny - 2 );
% end
for i = 1 : r * N 
    Y( i + Ny ) = 0.8033 * X( i + Ny )     + ...
                  1.6065* X( i + Ny - 1 )  + ...
                  0.8033 * X( i + Ny - 2 ) + ...
                  1.7332 * Y( i + Ny - 1 ) - ...
                  0.7510 * Y( i + Ny - 2 );
end
% for i = 1 : N 
%     YPulse1( i + Ny ) = 3.688 * XPulse1( i + Ny )     + ...
%                   7.376 * XPulse1( i + Ny - 1 )      + ...
%                   3.688 * XPulse1( i + Ny - 2 )      + ...
%                   1.488 * YPulse1( i + Ny - 1 )      - ...
%                   0.5099 * YPulse1( i + Ny - 2 );
% end
for i = 1 : N 
    YPulse( i + Ny ) =0.8033 * XPulse( i + Ny )          + ...
                      1.6065 * XPulse( i + Ny - 1 )      + ...
                      0.8033 * XPulse( i + Ny - 2 )      + ...
                      1.7332 * YPulse( i + Ny - 1 )      - ...
                      0.7510 * YPulse( i + Ny - 2 );
end
figure(4)
plot( 1:size( Y( Ny + 1 : r * N + Ny  ) ) , Y( Ny + 1 : r * N + Ny  ), 'r ' , t , u , 'b' ) ; 
Y1 = Y( Ny + ( r - 1 ) * N + 1  : r * N + Ny ) ;
X1 = X( Ny + ( r - 1 ) * N + 1  : r * N + Ny ) ; 
YSum = 0 ;
for i = 1 : N 
    YSum = YSum + Y1( i ) ; 
end
YAvr = YSum / N ;
Y1 = Y1 - YAvr ;%减去直流分量
Rmz = zeros( N , 1) ;
%计算互相关矩阵，输入与输出的互相关矩阵，进行卷积
for i = 1 : N 
    Rmz( i )= 0 ; 
    sum = 0 ;
    for j = 1 : N
        if( j >= i )
            sum = sum + X1( j - i + 1 ) * Y1( j ) ;
        else
            sum = sum + X1( N - ( i - j ) + 1 )*Y1( j ) ; 
        end 
    end
    Rmz( i ) = sum / N  ;
end
c = -Rmz( N ) ;
gK = ( N * ( Rmz + c ))/( ( N + 1 ) * ( a ^ 2 ) )
gY = impz( bz1,az1 ,50,1) ;
figure(1)
plot( 1 : N , gK , 'r')

%通过Hankel矩阵进行模型的辨识
Nsys = 2 ;%待辨识的系统的系统的阶次
Gsys1 = zeros( Nsys , Nsys ) ; 
Asys1 = zeros( Nsys , 1 ) ; 
Gsys2 = zeros( Nsys , 1 ) ; 
%注意Gsys是从1开始的
for i = 1 : Nsys
    for j = 1 : Nsys
        Gsys1( i , j ) = gK( i + j ) ;
    end
    Gsys2( i ) = -gK( Nsys + i + 1 ) ; 
end
Asys1 = inv( Gsys1 ) * Gsys2 
Bsys1 = zeros( Nsys + 1 , 1 ) ; 
Gsys2 = [ gK( 1 : Nsys + 1 ) ] ;
Asys2 = eye(Nsys + 1 ) ;
for i = 2 : Nsys + 1
     Asys2( i , : ) = [ Asys1( Nsys - ( i - 2 ):Nsys )' , Asys2( i , i : Nsys + 1 ) ] ; 
end
Asys2; 
Gsys2;
Bsys1 = Asys2 * Gsys2 ;
Aresult = [ 1 , flip( Asys1' ) ];
Bsys1 
Asys1
GY1 = impz( Bsys1 ,[ 1 , flip( Asys1' ) ] , 50 , 1);
figure(2);
% plot( 1 : size(gY) , gY , 'r' , 1 : size(YPulse) , YPulse , 'b', 1:size(YPulse1),YPulse1,'g');
plot( 1 : N , gK , 'r' , 1 : size(GY1) , GY1 , 'b');

参考书籍：
系统辨识理论及应用

知识网站：
https://wenku.baidu.com/view/e4e37083581b6bd97f19ea91.html

最后

以上就是愉快魔镜为你收集整理的matlab使用相关分析法和hankel矩阵法进行系统辨识的全部内容，希望文章能够帮你解决matlab使用相关分析法和hankel矩阵法进行系统辨识所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(44)

相关文章

Matlab中inv函数的使用
Matlab中inv函数的使用
Matlab之inv函数
Matlab之inv函数
for语句
for语句
参数模型matlab,[转载]matlab滤波器设计的参数建模方法
参数模型matlab,[转载]matlab滤波器设计的参数建模方法
matlab使用相关分析法和hankel矩阵法进行系统辨识
matlab使用相关分析法和hankel矩阵法进行系统辨识
基于matlab的频域辨识,频域辨识简介.ppt
基于matlab的频域辨识,频域辨识简介.ppt
matlab使用invfreqs出错,matlab中butter
matlab使用invfreqs出错,matlab中butter
矩阵方阵matlab,求助！！错误使用 inv 矩阵必须为方阵。
矩阵方阵matlab,求助！！错误使用 inv 矩阵必须为方阵。

评论列表共有 0 条评论

立即
投稿
返回
顶部