OFDM即正交频分复用(Orthogonal Frequency Division Multiplexing),是多载波调制的一种,通俗来说就是通过多条互相没有关系的通道传输不同的信息。OFDM现在主要用于4G通信上,并且由于其频带利用率高,抗多径能力强,能有效抑制ISI(符号间干扰)和ICI(信道间干扰),在水声通信方面也有较多的应用,这是后话。今天主要整理下OFDM原理上的一些东西,也理一理比较杂乱的大脑。
刚提到说OFDM的频带利用率高,抗多径能力强,那么对于OFDM的原理应该分以下几个部分进行说明:
1、子载波的正交性
2、OFDM与傅里叶变换的关系
3、抗多径、抑制ISI和ICI的原因及循环前缀
一、子载波的正交性
什么是正交?从向量上来看就是两个互相垂直的向量,无论其模长是多少,相乘总是等于0:
而在函数上的正交性是怎样的呢?用文字来说,就是无论两个函数的幅值为多少,在确定的一个时间周期内相乘,其积分总是等于0(也就是面积相加为0)。比如最简单的一对正交函数sin(t)和sin(2t)(matlab实在不熟练,画个图还要百度半天,干脆也截图下来好了):
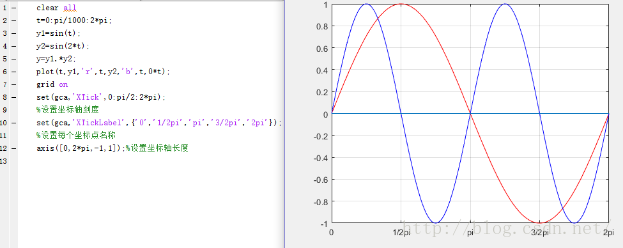
其中红色是sin(t),蓝色是sin(2t)。他们均在2π时间内具有完整的周期,各自在2π时间内的积分问为0(正负面积相加为0)。而sint(t)*sin(2t)的图像为:
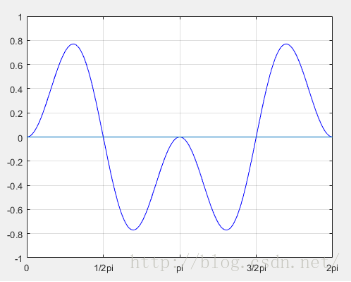
可以大概地看出,图像中正负面积相加同样为0,也就是:

再总结一遍,函数的正交性就是无论两个函数的幅值为多少,在确定的一个时间周期内相乘,其积分总是等于0。那么如果使得sin(t)的幅度为a,sin(2t)的幅度为b,也就是将a调制于sin(t),将b调制于sin(2t),同时传输这两个调制了信号的正弦波(子载波):a*sin(t)+b*sin(2t),在接收时又分别对两路子载波进行积分,也就是:
看,这样就将原始信息a和b解调出来了,两路子载波互不干扰,而OFDM就是通过多路互不干扰的子载波传递了不同的信息。而由于子载波的正交性,其频率间隔很小,使得频带利用率很高,在水声信道这样可用频带窄的环境中较为适用。
设f0~fN-1是以Δf(能使每个子载波互相正交的频率间隔)为频率间隔的N个频率,Nc为用到的子载波个数,那么就有: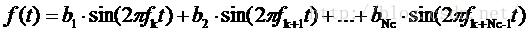
由于正弦函数与余弦函数的正交关系,上式还可以扩展为:
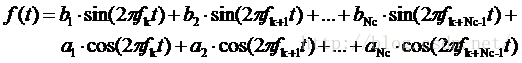
画个常见于各种OFDM原理说明文章内的框图来说,就是这样:
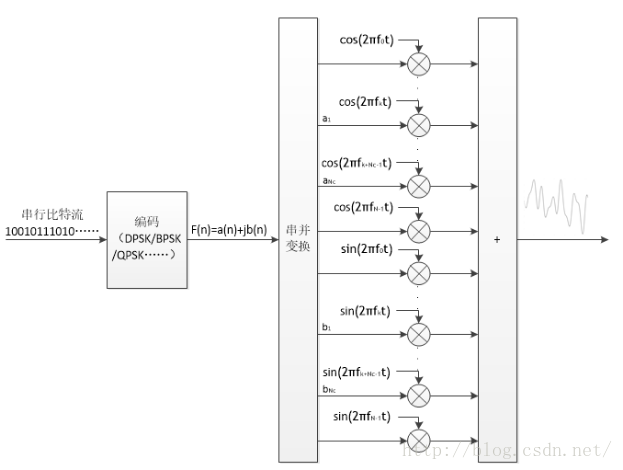
其中,F(n)是串行比特流经过编码后(按照不同的映射方式),产生的复数形式的数据流,a和b均为-1(也就是二进制的0)或1。F(n)中的实数a(n)调制于余弦子载波上,复数b(n)调制于正弦子载波上(三角函数的复数形式ej2πft=cos(2πft)+jsin(2πft))。在N个频率中,只有Nc个子载波是用于传递信息(这里说得有点绕,暂且理解处理过程即可)。之后将所有路的信号进行叠加,就成为了传递出去的波形了。在接收端,对各路信号进行积分,便解调出了a(n)和b(n)。
二、OFDM与傅里叶变换的关系
OFDM系统在处理的过程中要用到傅里叶变换,也是让很多人知其然不知其所以然的一个问题。将刚才的f(t)改写为复数形式,也就是:
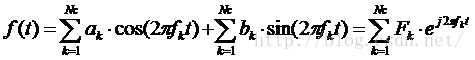
查一下傅里叶变换的公式,是不是特别像?傅里叶变换(FFT)就是将时域的波形转换为频域来看,频域上显示出来的各频率的幅度就是所调制的信号,逆傅里叶变换(IFFT)就是将调制了信号的各频率值合成为时域上的波形的过程,自然从公式上看是一样的了。所以,调制的过程就是逆傅里叶变换的过程,解调的过程就是傅里叶变换的过程。
上面复数表达式我认为可以这样理解,在一个子载波上(正余弦只不过是相位上的差别),而Fk即之前的F(n)=a(n)+jb(n),也就是一个子载波上可以携带2比特数据(具体携带1个还是2个与编码映射有关,本文以QPSK为例,也就是携带2比特)。
那么之前为什么要绕半天又N又Nc又k的呢?这个就跟IFFT的处理过程有关了,干脆以一个实例来说最明白不过:
1、假设我们取IFFT的点数N=2048;
2、输出通带为6~12kHz;
3、(IFFT变换后的)采样频率设置为fs=48kHz(根据采样定理,fs要大于2倍的最高频率)。
那么从以上三条我们可以知道什么呢?
1、第0个点(n=0)是零频,也就是直流;
2、第1024个点(n=N/2)对应的频率是24k(fs/2),以此为界,第1~2047个点是对称的,对称的原因嘛,看傅里叶变换的原理去(其实我也说不清,证明过程貌似有点复杂);
3、频率间隔Δf=fs/N=23.4375Hz,合着上一条一起看,也就是把48k平均分成了2048份,每一份之间的频率间隔为23.4375Hz(而实际上有意义的只有n<=1024);
4、算得6k对应n=f1/Δf=256,12k对应n=f2/Δf=512,因此Nc必须小于256,并且n的取值范围要在[256,512]内,否则输出的频率将高于或低于输出通带,这里以Nc=128为例,中心频率为9k,则n的取值为[320,448);
5、从时域上来看,可以知道采样周期Ts=1/fs=20.83μs,符号周期T=N*Ts=42.67ms,也就是频域上分了2048份,在时域上也采样了2048次;
6、这个符号周期指的就是一次IFFT变换需要的时间,也就是对于128个子载波,每个子载波分别在T时间内传输了一个复数符号(2bits),并且叠加在了一起,把256bits的数据发射了出去;
7、进一步地,假设声码器的码率为600bps(每45bits/75ms),要保证发射出去的速率与声码器一致,而我们现在的速率为每6kbps(256bits/42.67ms),怎么办呢?那就需要在每次IFFT变换之间留有间隔,为Tcp=256bits/600bps-42.67ms=384ms,这么长的时间间隔就这么空着吗?当然不,这就涉及到循环前缀,将在第三节说明。
整理一下涉及到的公式:
1、采样频率:fs>2*fmax
2、频率间隔:Δf=fs/N
3、有用子载波个数Nc<(f2/Δf-f1/Δf)
4、有用子载波取值范围[f1/Δf,f2/Δf)
5、频率与n值的对应关系:n=f/Δf
6、符号周期:T=N*Ts=N/fs
7、码率=Nc*2/(T+Tcp)(是否乘2根据一个复数符号携带1bit还是2bits而定)
三、抗多径、抑制ISI和ICI的原因及循环前缀
说到OFDM的抗多径能力就不得不说到循环前缀。多径干扰会产生时延扩展、信号衰落,简单说就是对于一个脉冲信号,经过了多径信道传输后,产生了多个具有时延的,有一定衰落的脉冲信号,这些信号幅度服从瑞利分布:
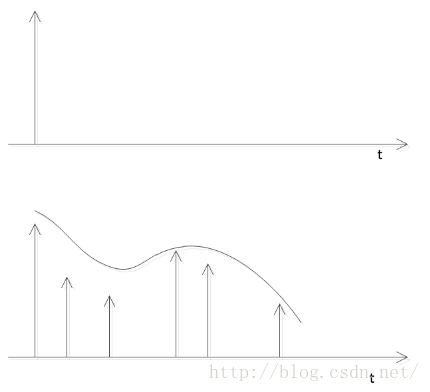
对于ISI(符号间干扰),只要前一个符号的时延扩展时间(信道冲激响应长度)不会影响到下一个符号,便可以消除ISI,也就是说每个符号之间的保护间隔时间要大于时延扩展的时间。
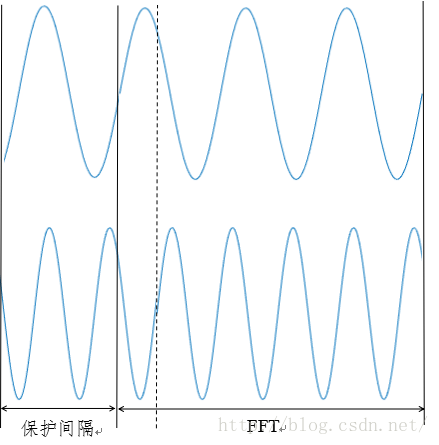
对于ICI(信号间干扰),就要谈到循环前缀(CP)。由于我们的信道是多径信道,各路子载波被接收到的时间可能有偏差,这就造成在FFT积分时间长度内子载波之间相差不再是整数周期,子载波之间的正交性受到破坏,如果保护间隔中只是单纯地填零,那么在解调时子载波之间就会产生干扰。循环前缀是将符号尾部的信号搬移到前方构成的,这样,就可以保证各路子载波在一次FFT积分时间长度内,各子载波之间相差总是整数个周期,避免了信号间的干扰。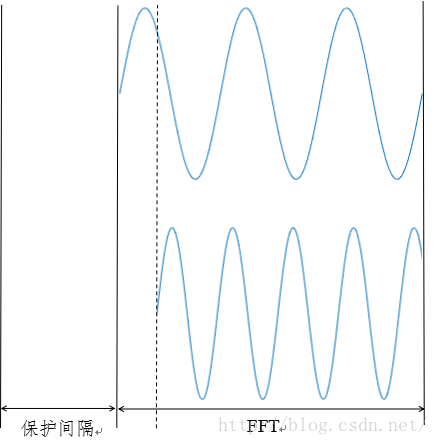
最后
以上就是灵巧美女最近收集整理的关于LTE关键技术之一:OFDMA(OFDM基本原理及简单实例应用)的全部内容,更多相关LTE关键技术之一内容请搜索靠谱客的其他文章。








发表评论 取消回复