A Minutes Before the New Year

Problem Description

New Year is coming and you are excited to know how many minutes remain before the New Year. You know that currently the clock shows h hours and m minutes, where 0≤hh<24 and 0≤mm<60. We use 24-hour time format!
Your task is to find the number of minutes before the New Year. You know that New Year comes when the clock shows 0 hours and 0 minutes.
You have to answer t independent test cases.

Input

The first line of the input contains one integer t (1≤t≤1439) — the number of test cases.
The following t lines describe test cases. The i-th line contains the time as two integers h and m (0≤h<24, 0≤m<60). It is guaranteed that this time is not a midnight, i.e. the following two conditions can’t be met at the same time: h=0 and m=0. It is guaranteed that both h and m are given without leading zeros.

Output

For each test case, print the answer on it — the number of minutes before the New Year.

Example

input
5
23 55
23 0
0 1
4 20
23 59
output
5
60
1439
1180
1

思路

水题。

Code

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef vector<int> VI;
typedef vector<VI> VII;
typedef vector<VII> VIII;

#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)

const int N = 2e5+5e4+5;

int main()
{
    int n;
    cin >> n;
    while(n --)
    {
        int hh, mm;
        cin >> hh >> mm;
        cout << (60-mm) + 60*(23-hh) << endl;
    }
    return 0;
}

B Candies Division

Problem Description

Santa has n candies and he wants to gift them to k kids. He wants to divide as many candies as possible between all k kids. Santa can’t divide one candy into parts but he is allowed to not use some candies at all.
Suppose the kid who recieves the minimum number of candies has a candies and the kid who recieves the maximum number of candies has b candies. Then Santa will be satisfied, if the both conditions are met at the same time:
b−a≤1 (it means b=a or b=a+1);
the number of kids who has a+1 candies (note that a+1 not necessarily equals b) does not exceed ⌊k2⌋ (less than or equal to ⌊k2⌋).
⌊k2⌋ is k divided by 2 and rounded down to the nearest integer. For example, if k=5 then ⌊k2⌋=⌊52⌋=2.
Your task is to find the maximum number of candies Santa can give to kids so that he will be satisfied.
You have to answer t independent test cases.

Input

The first line of the input contains one integer t (1≤t≤5⋅104) — the number of test cases.
The next t lines describe test cases. The i-th test case contains two integers n and k (1≤n,k≤109) — the number of candies and the number of kids.

Output

For each test case print the answer on it — the maximum number of candies Santa can give to kids so that he will be satisfied.

Example

input
5
5 2
19 4
12 7
6 2
100000 50010
output
5
18
10
6
75015

Note

In the first test case, Santa can give 3 and 2 candies to kids. There a=2,b=3,a+1=3.
In the second test case, Santa can give 5,5,4 and 4 candies. There a=4,b=5,a+1=5. The answer cannot be greater because then the number of kids with 5 candies will be 3.
In the third test case, Santa can distribute candies in the following way: [1,2,2,1,1,2,1]. There a=1,b=2,a+1=2. He cannot distribute two remaining candies in a way to be satisfied.
In the fourth test case, Santa can distribute candies in the following way: [3,3]. There a=3,b=3,a+1=4. Santa distributed all 6 candies.

思路

水题。

Code

#include <bits/stdc++.h>
 
using namespace std;
 
typedef long long ll;
typedef vector<int> VI;
typedef vector<VI> VII;
typedef vector<VII> VIII;
typedef pair<int, int> PII;
 
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
 
const int N = 1e6 + 5;
const ll MOD = 1e9 + 7;
 
int main()
{
    int T;
    scanf("%d" ,&T);
    while(T --)
    {
        int n, k;
        scanf("%d%d", &n, &k);
        printf("%dn", min((n/k+1)*(k/2)+(n/k)*(k-k/2), n));
    }
    return 0;
}

C Friends and Gifts

Problem Description

There are n friends who want to give gifts for the New Year to each other. Each friend should give exactly one gift and receive exactly one gift. The friend cannot give the gift to himself.
For each friend the value fi is known: it is either fi=0 if the i-th friend doesn’t know whom he wants to give the gift to or 1≤fi≤n if the i-th friend wants to give the gift to the friend fi.
You want to fill in the unknown values (fi=0) in such a way that each friend gives exactly one gift and receives exactly one gift and there is no friend who gives the gift to himself. It is guaranteed that the initial information isn’t contradictory.
If there are several answers, you can print any.

Input

The first line of the input contains one integer n (2≤n≤2⋅105) — the number of friends.
The second line of the input contains n integers f1,f2,…,fn (0≤fi≤n, fi≠i, all fi≠0 are distinct), where fi is the either fi=0 if the i-th friend doesn’t know whom he wants to give the gift to or 1≤fi≤n if the i-th friend wants to give the gift to the friend fi. It is also guaranteed that there is at least two values fi=0.

Output

Print n integers nf1,nf2,…,nfn, where nfi should be equal to fi if fi≠0 or the number of friend whom the i-th friend wants to give the gift to. All values nfi should be distinct, nfi cannot be equal to i. Each friend gives exactly one gift and receives exactly one gift and there is no friend who gives the gift to himself.
If there are several answers, you can print any.

Examples

input
5
5 0 0 2 4
output
5 3 1 2 4

input
7
7 0 0 1 4 0 6
output
7 3 2 1 4 5 6

input
7
7 4 0 3 0 5 1
output
7 4 2 3 6 5 1

input
5
2 1 0 0 0
output
2 1 4 5 3

思路

构造。
把所有没有收到礼物的人加入队列，然后考虑送礼物。没有明确送礼物的人从队列里取出一个人，如果是自己，就放回队列重新取。最后如果队列里只有自己了，就从初始没有明确送礼物的人里面随便选择一个，把送给的人交换。

Code

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef vector<int> VI;
typedef vector<VI> VII;
typedef vector<VII> VIII;
typedef pair<int, int> PII;

#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)

const int N = 2e5 + 5;
const ll MOD = 1e9 + 7;

int flag[N];
int give[N];
int gett[N];
queue<int> Q;

int num = 0;

int main()
{
    int n;
    scanf("%d", &n);
    rep(i,1,n)
    {
        int x;
        scanf("%d", &x);
        flag[i] = x;
        give[i] = x;
        if(x != 0)
            gett[x] = i;
        else
            num ++;
    }
    rep(i,1,n)
    {
        if(gett[i] == 0)
            Q.push(i);
    }
    int pos = 1;
    rep(i,1,n)
    {
        if(give[i] == 0)
        {
            pos = i;
            while(give[pos] == 0)
            {
                give[pos] = Q.front();
                Q.pop();
                if(pos == give[pos])
                {
                    Q.push(pos);
                    give[pos] = Q.front();
                    Q.pop();
                }
                pos = give[pos];
                num --;
            }
        }
    }
    rep(i,1,n)
    {
        if(give[i] == i)
        {
            rep(j,1,n)
            {
                if(flag[j] == 0)
                {
                    swap(give[i], give[j]);
                    break;
                }
            }
        }
    }
    rep(i,1,n)
    {
        printf("%d ", give[i]);
    }
    printf("n");
    return 0;
}

D Christmas Trees

Problem Description

There are n Christmas trees on an infinite number line. The i-th tree grows at the position xi. All xi are guaranteed to be distinct.
Each integer point can be either occupied by the Christmas tree, by the human or not occupied at all. Non-integer points cannot be occupied by anything.
There are m people who want to celebrate Christmas. Let y1,y2,…,ym be the positions of people (note that all values x1,x2,…,xn,y1,y2,…,ym should be distinct and all yj should be integer). You want to find such an arrangement of people that the value ∑j=1mmini=1n|xi−yj| is the minimum possible (in other words, the sum of distances to the nearest Christmas tree for all people should be minimized).
In other words, let dj be the distance from the j-th human to the nearest Christmas tree (dj=mini=1n|yj−xi|). Then you need to choose such positions y1,y2,…,ym that ∑j=1mdj is the minimum possible.

Input

The first line of the input contains two integers n and m (1≤n,m≤2⋅105) — the number of Christmas trees and the number of people.
The second line of the input contains n integers x1,x2,…,xn (−109≤xi≤109), where xi is the position of the i-th Christmas tree. It is guaranteed that all xi are distinct.

Output

In the first line print one integer res — the minimum possible value of ∑j=1mmini=1n|xi−yj| (in other words, the sum of distances to the nearest Christmas tree for all people).
In the second line print m integers y1,y2,…,ym (−2⋅109≤yj≤2⋅109), where yj is the position of the j-th human. All yj should be distinct and all values x1,x2,…,xn,y1,y2,…,ym should be distinct.
If there are multiple answers, print any of them.

Examples

input
2 6
1 5
output
8
-1 2 6 4 0 3

input
3 5
0 3 1
output
7
5 -2 4 -1 2

思路

暴力。
先把x[i]左边1和右边1的点放上人（如果没有树也没有人的话），然后左边2和右边2的点，以此类推。

Code

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef vector<int> VI;
typedef vector<VI> VII;
typedef vector<VII> VIII;
typedef pair<int, int> PII;

#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)

const int N = 2e5 + 5;
const ll MOD = 1e9 + 7;

struct S
{
    int pos;
    int len;
};

int x[N];
VI G;
map<int, int> VIS;
queue<S> Q;
ll ans;

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    rep(i,1,n)
    {
        scanf("%d", &x[i]);
        VIS[x[i]]=1;
    }
    rep(i,1,n)
    {
        if(VIS.count(x[i]-1)==false)
        {
            Q.push(S{x[i]-1, 1});
            VIS[x[i]-1] = 1;
        }
        if(VIS.count(x[i]+1)==false)
        {
            Q.push(S{x[i]+1, 1});
            VIS[x[i]+1] = 1;
        }
    }
    while(m --)
    {
        S now = Q.front();
        Q.pop();
        G.push_back(now.pos);
        ans += now.len;
        if(VIS.count(now.pos-1)==false)
        {
            Q.push(S{now.pos-1, now.len+1});
            VIS[now.pos-1] = 1;
        }
        if(VIS.count(now.pos+1)==false)
        {
            Q.push(S{now.pos+1, now.len+1});
            VIS[now.pos+1] = 1;
        }
    }
    printf("%I64dn", ans);
    int sz = G.size();
    rep(i,0,sz-1)
    {
        printf("%d ", G[i]);
    }
    printf("n");
    return 0;
}

E New Year Parties

Problem Description

Oh, New Year. The time to gather all your friends and reflect on the heartwarming events of the past year…
n friends live in a city which can be represented as a number line. The i-th friend lives in a house with an integer coordinate xi. The i-th friend can come celebrate the New Year to the house with coordinate xi−1, xi+1 or stay at xi. Each friend is allowed to move no more than once.
For all friends 1≤xi≤n holds, however, they can come to houses with coordinates 0 and n+1 (if their houses are at 1 or n, respectively).
For example, let the initial positions be x=[1,2,4,4]. The final ones then can be [1,3,3,4], [0,2,3,3], [2,2,5,5], [2,1,3,5] and so on. The number of occupied houses is the number of distinct positions among the final ones.
So all friends choose the moves they want to perform. After that the number of occupied houses is calculated. What is the minimum and the maximum number of occupied houses can there be?

Input

The first line contains a single integer n (1≤n≤2⋅105) — the number of friends.
The second line contains n integers x1,x2,…,xn (1≤xi≤n) — the coordinates of the houses of the friends.

Output

Print two integers — the minimum and the maximum possible number of occupied houses after all moves are performed.

Examples

input
4
1 2 4 4
output
2 4

input
9
1 1 8 8 8 4 4 4 4
output
3 8

input
7
4 3 7 1 4 3 3
output
3 6

Note

In the first example friends can go to [2,2,3,3]. So friend 1 goes to x1+1, friend 2 stays at his house x2, friend 3 goes to x3−1 and friend 4 goes to x4−1. [1,1,3,3], [2,2,3,3] or [2,2,4,4] are also all valid options to obtain 2 occupied houses.
For the maximum number of occupied houses friends can go to [1,2,3,4] or to [0,2,4,5], for example.

思路

最小值就是三个一组，每出现一个位置有人，则可以和它附近的连续三个点合并。
最大值，对于每一个有人的位置，假设位置为pos，则优先考虑pos-1的点，若pos-1的点没有人，则将pos这个点的人分一个到pos-1；然后再看pos点有没有人，如果还有人，则留一个在pos点；再看还有没有多余的人，要有，则放在pos+1的点上。遍历即可。

Code

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef vector<int> VI;
typedef vector<VI> VII;
typedef vector<VII> VIII;
typedef pair<int, int> PII;

#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)

const int N = 2e5 + 5;
const ll MOD = 1e9 + 7;

int x[N];
int vis[N];
int tol[N];

int main()
{
    int n;
    scanf("%d", &n);
    rep(i,1,n)
    {
        scanf("%d", &x[i]);
        tol[x[i]]++;
    }
    int minn = 0, maxn = 0;
    rep(i,1,n)
    {
        if(tol[i] != 0)
        {
            minn ++;
            i += 2;
        }
    }
    rep(i,1,n)
    {
        if(tol[i])
        {
            if(!vis[i-1])
            {
                maxn ++;
                tol[i] --;
                vis[i-1] = 1;
            }
        }
        if(tol[i])
        {
            if(!vis[i])
            {
                maxn ++;
                tol[i] --;
                vis[i] = 1;
            }
        }
        if(tol[i])
        {
            if(!vis[i+1])
            {
                maxn ++;
                tol[i] --;
                vis[i+1] = 1;
            }
        }
    }
    printf("%d %dn", minn, maxn);
    return 0;
}

F DIY Garland

Problem Description

Polycarp has decided to decorate his room because the New Year is soon. One of the main decorations that Polycarp will install is the garland he is going to solder himself.
Simple garlands consisting of several lamps connected by one wire are too boring for Polycarp. He is going to solder a garland consisting of n lamps and n−1 wires. Exactly one lamp will be connected to power grid, and power will be transmitted from it to other lamps by the wires. Each wire connectes exactly two lamps; one lamp is called the main lamp for this wire (the one that gets power from some other wire and transmits it to this wire), the other one is called the auxiliary lamp (the one that gets power from this wire). Obviously, each lamp has at most one wire that brings power to it (and this lamp is the auxiliary lamp for this wire, and the main lamp for all other wires connected directly to it).
Each lamp has a brightness value associated with it, the i-th lamp has brightness 2i. We define the importance of the wire as the sum of brightness values over all lamps that become disconnected from the grid if the wire is cut (and all other wires are still working).
Polycarp has drawn the scheme of the garland he wants to make (the scheme depicts all n lamp and n−1 wires, and the lamp that will be connected directly to the grid is marked; the wires are placed in such a way that the power can be transmitted to each lamp). After that, Polycarp calculated the importance of each wire, enumerated them from 1 to n−1 in descending order of their importance, and then wrote the index of the main lamp for each wire (in the order from the first wire to the last one).
The following day Polycarp bought all required components of the garland and decided to solder it — but he could not find the scheme. Fortunately, Polycarp found the list of indices of main lamps for all wires. Can you help him restore the original scheme?

Input

The first line contains one integer n (2≤n≤2⋅105) — the number of lamps.
The second line contains n−1 integers a1, a2, …, an−1 (1≤ai≤n), where ai is the index of the main lamp for the i-th wire (wires are numbered in descending order of importance).

Output

If it is impossible to restore the original scheme, print one integer −1.
Otherwise print the scheme as follows. In the first line, print one integer k (1≤k≤n) — the index of the lamp that is connected to the power grid. Then print n−1 lines, each containing two integers xi and yi (1≤xi,yi≤n, xi≠yi) — the indices of the lamps connected by some wire. The descriptions of the wires (and the lamps connected by a wire) can be printed in any order. The printed description must correspond to a scheme of a garland such that Polycarp could have written the list a1, a2, …, an−1 from it. If there are multiple such schemes, output any of them.

Example

input
6
3 6 3 1 5
output
3
6 3
6 5
1 3
1 4
5 2

Note

The scheme for the first example (R denotes the lamp connected to the grid, the numbers on wires are their importance values):

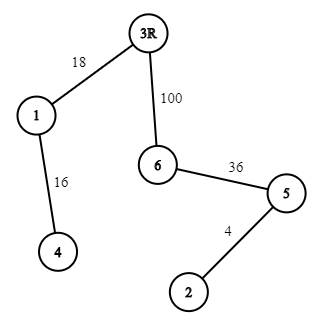
思路

首先我们可以知道，a数组里面没有出现过的数字（不为父节点）的就是叶节点。由于题意保证必定有解，所以我们可以知道亮度最小的灯泡应该接在重要性最低的电线上。用优先队列暴力即可。

Code

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef vector<int> VI;
typedef vector<VI> VII;
typedef vector<VII> VIII;
typedef pair<int, int> PII;

#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)

const int N = 2e5 + 5;
const ll MOD = 1e9 + 7;

int a[N];
int sz[N];
vector<PII> ANS;

int main()
{
    int n;
    scanf("%d", &n);
    rep(i,1,n-1)
    {
        scanf("%d", &a[i]);
        sz[a[i]] ++;
    }
    printf("%dn", a[1]);
    priority_queue<int, VI, greater<int> > Q;
    rep(i,1,n)
    {
        if(sz[i] == 0)
            Q.push(i);
    }
    int cnt = n - 1;
    while(cnt != 0)
    {
        int x, y;
        x = Q.top();
        Q.pop();
        y = a[cnt--];
        ANS.push_back(make_pair(y, x));
        sz[y] --;
        if(sz[y] == 0)
            Q.push(y);
    }
    int szz = ANS.size();
    per(i,szz-1,0)
    {
        printf("%d %dn", ANS[i].first, ANS[i].second);
    }
    return 0;
}

（完）

最后

以上就是敏感钢铁侠为你收集整理的Codeforces Round #611 (Div. 3) - BenFromHRBUSTA Minutes Before the New YearB Candies DivisionC Friends and GiftsD Christmas TreesE New Year PartiesF DIY Garland（完）的全部内容，希望文章能够帮你解决Codeforces Round #611 (Div. 3) - BenFromHRBUSTA Minutes Before the New YearB Candies DivisionC Friends and GiftsD Christmas TreesE New Year PartiesF DIY Garland（完）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。