1.简述意义
在我进行课程仿真时候,我发现网上针对串行干扰抵消算法的中文内容还是比较少的,因此我个人想将看完文章后自己的理解写上来,希望对一些同学有点帮助,串行干扰抵消算法还是很经典的,它不仅可以用于解调多发射天线的内容,而且它也可以用于上行时隙的多用户检测,所以说它是比较经典的,下面我就大概叙述一下这次文章内容。
2.概述
根据论文要求,对一个8发12收(发射天线数要低于接收天线数,使得通过模型得到的方程为超定方程,同时,程序里面的发射天线和接收天线是可以修改的)的V-BLAST系统进行基带仿真。发射端采用8路V-BLAST发射天线,发射信号采用不同调制,不考虑信道编码;发射信号经过平坦Rayleigh衰落信道,同时默认信道变化的很慢,即它是一个慢衰落信道即信道的相干时间大于码元持续时间,接收端默认进行了信道估计,在已知H的情况下使用不同的接收机检测方案(MMSE、ZF和SIC),对接收信号进行处理,绘制出误码率平均信噪比变化的曲线,并进行对比分析。
3.原理阐明
3.1MIMO信道模型
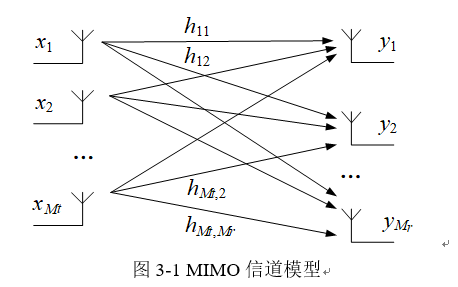
移动通信系统的性能在很大程度上决定于无线信道的特性。单发单收系统无线信道的特性已经研究得很透彻,针对其各通信标准所采用的载频、带宽、环境等都有权威机构给出实测的信道模型。对于多天线信道而言,许多单天线的概念都被继承了下来,如路径传播损耗、阴影衰落、多径衰落 损耗、长期衰落、短期衰落、相干时间、相干带宽、频率选择性衰落、平坦衰落等 , 所采用的信道模型也基本都是单天线情况下的一些拓展。本实验采用独立的慢衰落环境中的多输入多输出 MIMO 系统,假设发送端的天线数目为Mt,接收端端的天线数目为 Mr。用hij表示从第 j 个发射天线到第 i 个接收天线的信道增益。接收天线i处的噪声为ni,j=1,…, Mt ,i=1,…, Mr ;则第i个接收天线接收信号为:
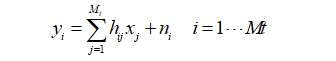
可以将信号模型写成矩阵的形式,MIMO信道模型如图3-1所示。
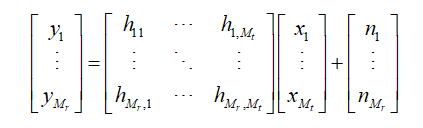
简记为![]() ,通常假设不同信道衰落系数hij为独立同分布的循坏对称复高斯随机变量,噪声ni也为独立同分布的循坏对称复高斯随机变量
,通常假设不同信道衰落系数hij为独立同分布的循坏对称复高斯随机变量,噪声ni也为独立同分布的循坏对称复高斯随机变量
3.2MIMO系统模型
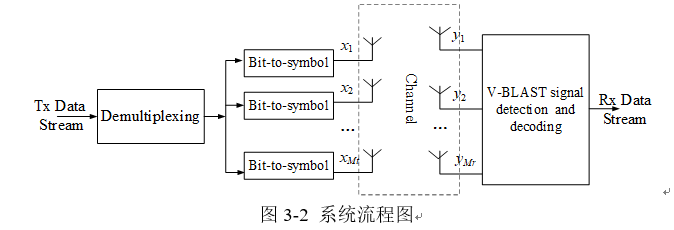
系统工作流程如图3-2下。首先V-BLAST系统在发射端通过串并转换将数据流分解为Mt个子数据流,然后使用 QPSK 或 16QAM 对各路子信号流进行调制, 将比特映射为符号;调制完成后,分别送到Mt个发射天线分别发射,在接收端用Mr个接收天线检测信号。这里假设不论有多少个发送天线,系统的总发射功率是不变的,且总发射功率是平均分配到各个天线的。在接收端用Mr个接收天线检测信号,并按照一定信号检测与估计的方法进行符号解调,最后恢复出数据流(各个接收天线单独进行信号处理得到子数据流,最后需要并串转换将子数据流合成为一个数据流)。假设发送天线之间、接收天线之间完全不相关,且发送的数据也互相独立。V-BLAST系统中接收天线的个数一般要大于或等于发送天线的个数。
关于接收机检测与估计的方法,最直接的最大似然估计在MIMO信道中可直接采用线性检测(按照ZF或MMSE准则),也可采用非线性的干扰抵消检测(如串行干扰抵消SIC)。
3.3 接收机检测方法
3.3.1迫零(ZF)算法

3.3.2迫零(ZF)算法


3.3.3串行干扰抵消(SIC-ZF)算法
串行干扰抵消算法是一种非线性检测算法。SIC的基本思想是在对多个符号进行检测与估计时,如果能先对某个符号进行检测与估计解出这个符号,则在解另一个符号时可将已解出的符号对当前待解符号的干扰消除,从而提高待解符号的SINR,提高检测与估计的误码码性能。对于Mt个发送符号,串行干扰抵消每次对一个符号进行检测与估计,每次检测时,先消掉前面已经解出的符号干扰,再对待解符号进行检测与估计(通常仍采用ZF或MMSE准则对待解符号做线性变换),根据论文,我们此次实验采用ZF准则做线性变换。因此对这Mt个发送符号在检测与估计时,共需要Mt步检测判决,(且除掉第一步,其他每一步检测之前都要利用已解出的符号做干扰抵消),这就存在对Mt个发送符号先对谁进行检测的排序问题。理论证明,当Mt个发送符号使用相同星座图时,每一步都选择接收SNR最大的符号,即对应最优的符号排序。
当采用ZF准则时,对应的SIC算法表示如下:



4.仿真结果
4.1仿真参数
| 参数类型 | 仿真参数 |
| 发射天线数 | 8 |
| 接收天线数 | 12 |
| 帧长 | 40000 |
| 总帧数 | 10 |
| 调制方式 | 16QAM/QPSK |
| 信道模型 | 理想瑞利信道 |
| 发射功率 | 恒为1 |
| 信噪比(dB) | 0:1:10 |
| 均衡算法 | ZF,MMSE,SIC |
4.2仿真结果
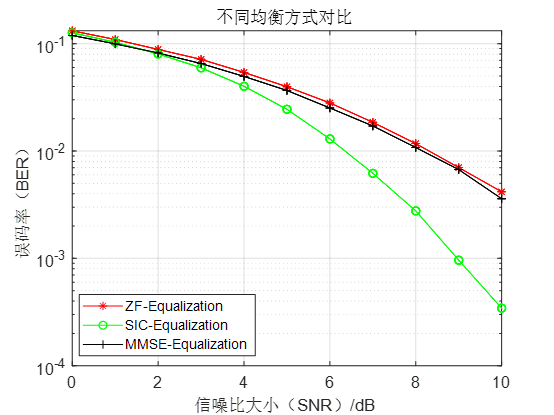
图4-1 16QAM调制下不同均衡方式误码率
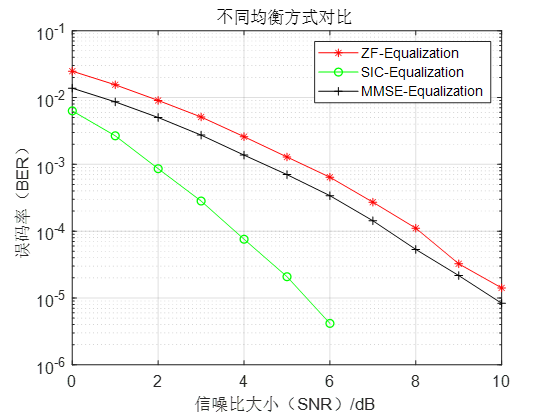
图4-2 QPSK调制下不同均衡方式误码率
4.3仿真分析
通过上述实验结果,对三种接收机检测方式进行分析,我们可以发现:在线性检测方式中,MMSE检测性略微优于ZF,但是优势表现并不明显。ZF虽然消除了符号间干扰同时放大了噪声,而MMSE考虑使得信号和噪声估计的均方误差最小的检测问题,其解的形式满足正交性原理,这是线性估计中性能最好的检测方式,当信噪比比较大时,ZF对噪声放大作用对检测信噪比影响相对削弱,ZF和MMSE在信噪比提高的条件下性能会更加接近一些。对比线性检测(ZF和MMSE)和非线性检测(SIC)可以看到,非线性检测性能可明显提高,SIC每一步操作都消除了已解信号干扰,再利用ZF准则进行检测,如果已解信号估计准确,消除已解信号干扰后检测的等效信干燥比提高明显,因此当信噪增大时,SIC误码性能提升效果明显。
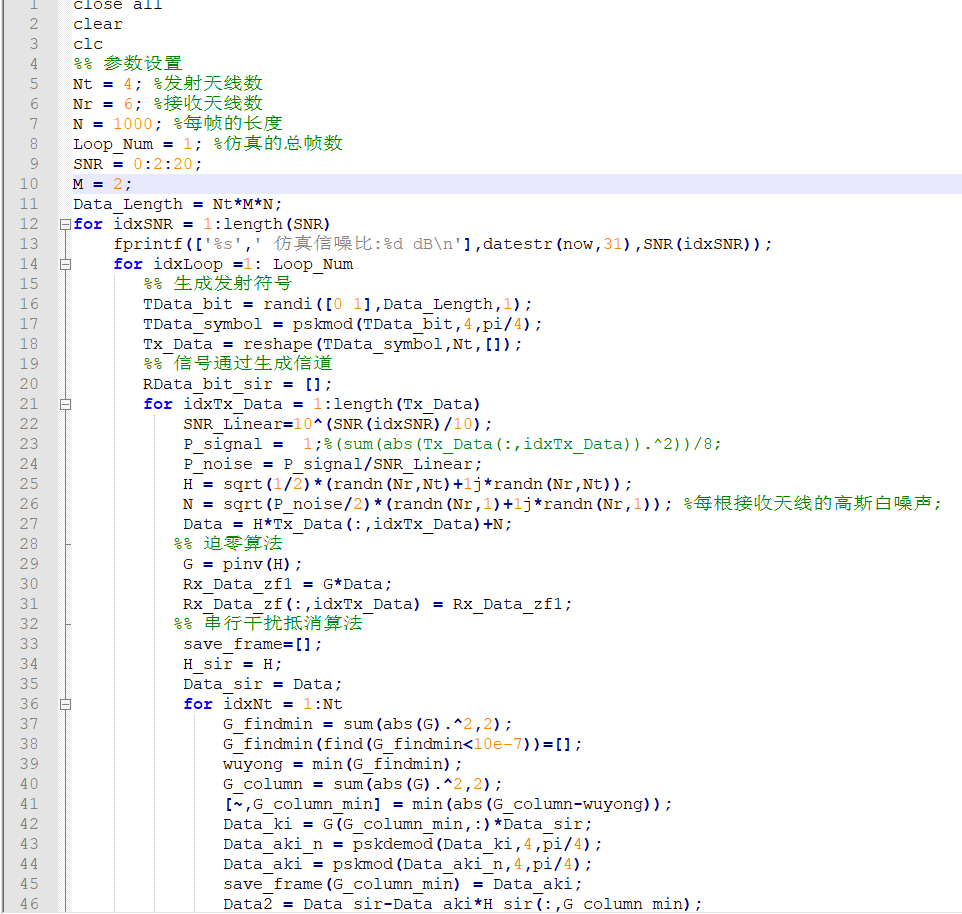
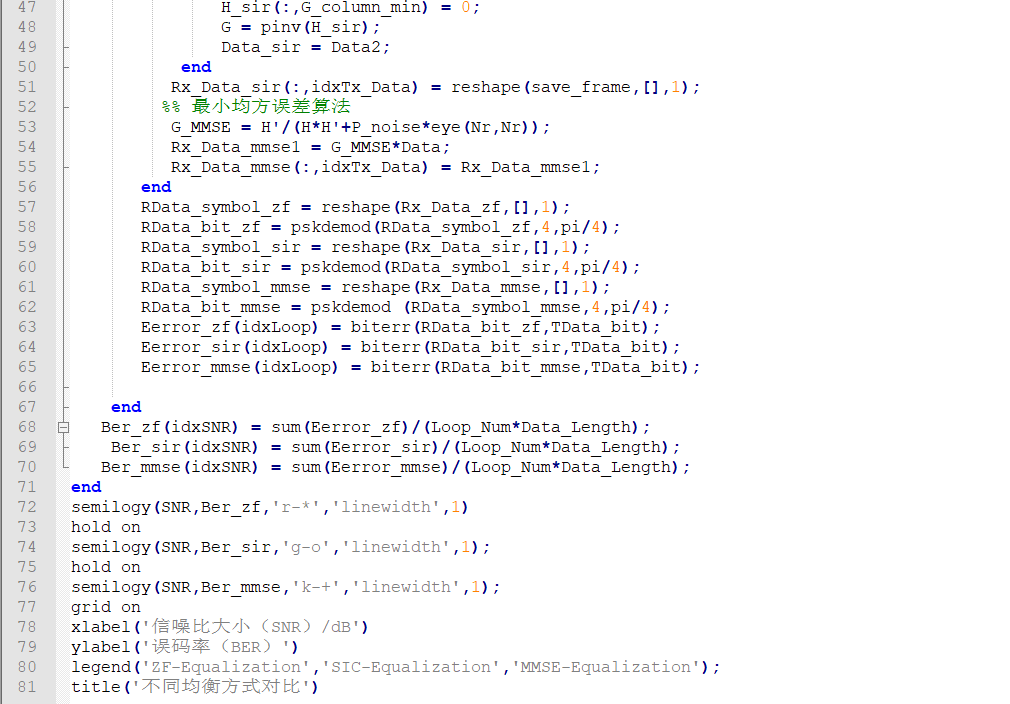
代码如下:
最后
以上就是背后大碗最近收集整理的关于基于Matlab的串行干扰抵消(SIC)算法(包含与MMSE,ZF的对比)的全部内容,更多相关基于Matlab内容请搜索靠谱客的其他文章。








发表评论 取消回复