阅读提醒

本文中的很多引用块对一些不影响本文理解且非本文重点的东西进行了详细说明和解释。第一遍阅读可以将其略过以抓住本文主线。但博主强烈建议热爱通信以及不想仅仅停留在"y=hx+n"层面的读者能够对这些引用块的内容进行二次阅读，当然这些东西只是我的一些个人理解，如有问题或错误，欢迎讨论交流！

问题背景和系统模型

一个单小区下行NOMA系统，一个基站BS使用相同的时频资源同时服务两个用户。假设用户2的信道增益大于用户1的信道增益，即$|h_2|>|h_1|$，并称用户1为弱用户，用户2为强用户。令$x_1,x_2$分别表示BS要传给两个用户的信号，且两者统计独立，则BS发送的信号为两个用户信号的叠加$x=x_1+x_2$。BS最大发射功率为
$$P=\mathbb{E}[|x{|}^2]=\mathbb{E}[|x_1{|}^2]+\mathbb{E}[|x_2{|}^2]=P_1+P_2\text{\hspace{1em}(1)}$$
假设两个用户接收端的噪声$n_k\sim \mathcal{C}\mathcal{N}(0,N_0),k=1,2$，则接收到的信号为
$$y_k=h_k\cdot x+n_k,k=1,2\text{\hspace{1em}(1)}$$

注意到在上面AWGN的分布中，用了$N_0$表示噪声方差（功率），而$N_0$一般表示的都是噪声的单边功率谱密度，这里用该符号表示噪声功率是因为$N_0$和噪声功率${\sigma }^2$的确存在关系。我们知道$N_0$是连续时间AWGN的单边功率谱密度（对于复高斯噪声，则表示每一维的单边功率谱密度均为$N_0$），而式(2)模型我们考虑的是一个离散化后的结果，离散化的过程实际上是通过匹配滤波和采样实现的，在本人的博客超级干货：BPSK/QPSK数字调制系统误码率MATLAB仿真中附录部分证明了以下关系（具体细节可以参考该博文）：

对于一维的情况即实高斯噪声时，离散化后的噪声功率
$${\sigma }^2=N_0/2$$

对于二维的情况即复高斯噪声时，离散化后的噪声功率为
$${\sigma }^2={\sigma }_I^2+{\sigma }_Q^2=N_0$$

当然也可以从另一个更加直观的角度去理解记忆，连续波形和离散符号与Nyquist第一准则密切相关，我们知道1Hz带宽上每秒可以无码间串扰的传输2个实符号或一个复数符号，那么一个实符号的功率为
$$\frac{1}{2}(Hz)\cdot N_0(W/Hz)=N_o/2(W)$$
而一个复数符号的功率为
$$1(Hz)\cdot N_0(W/Hz)=N_o(W)$$

在大多数文献中都会提到，我们应该为弱用户分配更多的功率且弱用户直接解调数据（即将强用户信号视为干扰），而强用户先解调出弱用户的数据，之后进行干扰消除，最后解调自己的数据。

这么做似乎也很容易理解和接受，因为弱用户信道增益低（路损高），需要分配更多功率以保证其基本的数据率需求（即要保证接收端足够大的信干噪比SINR）。这样分配的前提下，弱用户接收到的信号中自己信号的SINR更大，所以直接解调自己的数据即可；另一方面，既然弱用户都能把其自己的数据成功解调出来，那么在信道条件更好的强用户处必然也可以将其解调出来，将其对接收信号的影响去除掉之后便可解调强用户自己的数据。

从下行容量域的角度看问题

这篇博客将从下行NOMA容量域（capacity region）的角度来说明无论功率分配如何，强用户进行SIC（即上面提到的已经广为人知的方式）都要比弱用户进行SIC可以获得更高的可达速率。

弱用户进行SIC，即强用户直接解调其自己的数据，而弱用户先解调出强用户数据，并将其干扰消除，之后解调弱用户自己的数据。

如果SIC在强用户处进行，则有
$$R_1=\log \left(1+\frac{P_1\cdot |h_1{|}^2}{P_2\cdot |h_1{|}^2+N_0}\right),R_2=\log \left(1+\frac{P_2\cdot |h_2{|}^2}{N_0}\right)\text{\hspace{1em}(3)}$$
如果SIC在弱用户进行，则有
$$R_1^{\prime }=\log \left(1+\frac{P_1^{\prime }\cdot |h_1{|}^2}{N_0}\right),R_2^{\prime }=\log \left(1+\frac{P_2^{\prime }\cdot |h_2{|}^2}{P_1^{\prime }\cdot |h_2{|}^2+N_0}\right)\text{\hspace{1em}(4)}$$

上面的容量公式表示1Hz带宽可以达到的数据速率（考虑连续时间AWGN信道容量公式，将带宽为1Hz代入），单位为为bits/s/Hz。

也可以从离散AWGN信道容量公式的角度看，上面的香农容量公式前面没有1/2，是因为有1/2的那个表示的是发送一个实符号可以发送的比特数，即bits per real symbol，或者记为bits per dimmension (bits/1D)。而由Nyquist第一准则知1Hz带宽上，无码间串扰（ISI free）的最大符号速率是每秒传2个实数符号（考虑PAM），或一个复数符号（考虑IQ调制，实部虚部独立承载信息）,没有理由不用1Hz去传两个实符号。所以上面的容量公式也可以理解为因为传了两个独立的实符号因此乘了2得到。此时的单位为bits per complex symbol，或者记为bits per 2 dimmension (bits/2D)。显然 per complex symbol 或者 per 2 dimmension等价于per second per Hz，进而和上面第一个角度看的单位 bits/s/Hz统一了起来。

当然只有$x_1$和$x_2$均满足复高斯分布时上面的容量才可以达到。

下行容量域(界)仿真结果图

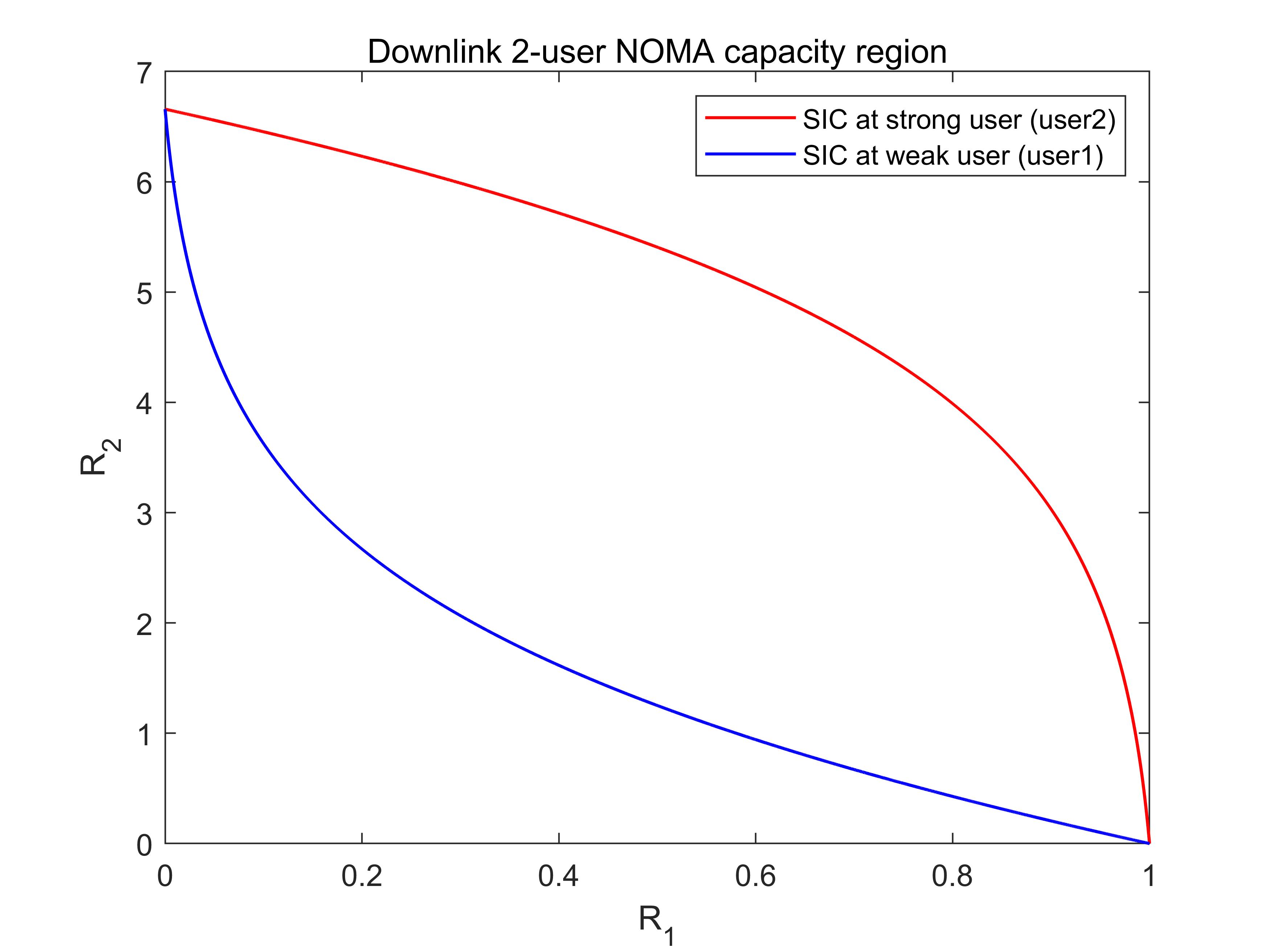
下面先给出以上两种SIC顺序下的下行容量域（界），相应的参数设置与Tse的《Fundamentals of Wireless Communication》一书中图6.9完全相同，具体的参数设置在下面的代码中也将详细给出并说明

仿真代码

% User1 is the weak user and user2 is the strong user, i.e., 
% abs(h1)<abs(h2).

% Define Delta(dB) = 20*log10(abs(h2)/abs(h1)) to characterize 
% the difference  between channel gains of the two users.
Delta = 20; 

% Always set single-side noise power spetrum density
% to 1 for convenience
N0 = 1;

% Always set channel gain of the strong user(i.e. user 2) 
% to 1 for convenience.
h2 = 1;

% Therefore channel gain of weak user(i.e. user 1) is
h1 = 10^(-Delta/20);

% set total power
P = N0/h1^2; % then maximum rate of user1 is 1 bits/2D(bits/s/Hz)

P1 = 0:0.01:P;
P2 = P-P1;

% SIC at strong user (user2)
R1 = log2(1+P1*h1^2./(P2*h1^2+N0));
R2 = log2(1+P2*h2^2./N0);

% SIC at weak user (user1)
R1_ = log2(1+P1*h1^2./N0);
R2_ = log2(1+P2*h2^2./(P1*h2^2+N0));

% plot
figure('Color', [1,1,1]);
hold on; box on;
plot(R1, R2, 'r-', R1_, R2_, 'b-', 'LineWidth', 1);
xlabel('R_1');
ylabel('R_2');
title('Downlink 2-user NOMA capacity region')
legend('SIC at strong user (user2)', 'SIC at weak user (user1)')

可以看出在强用户处进行SIC时的容量域边界完全包住了在弱用户处进行SIC。换句话说对任意的$(P_1^{\prime },P_2^{\prime })$得到的容量$(R_1^{\prime },R_2^{\prime })$，总可以找到一组$(P_1,P_2)$，其得到容量$(R_1,R_2)$，满足

$$R_1\ge R_1^{\prime },R_2\ge R_2^{\prime }$$

等号只在两种极端情况下（即功率全部分配给其中的一个用户）取到。

数学证明

下面对该结论进行数学证明，即证明当$R_1=R_1^{\prime }$时，必有$R_2>R_2^{\prime }$（极端情况取等号，下面不再考虑极端情况）

令$\alpha =\frac{N_0}{|h_1{|}^2},\beta =\frac{N_0}{|h_2{|}^2}$，易知$\alpha >\beta$，重写式(3)和(4)，有

$$R_1=\log \left(1+\frac{P_1}{P_2+\alpha }\right),R_2=\log \left(1+\frac{P_2}{\beta }\right)\text{\hspace{1em}(5)}$$

和

$$R_1^{\prime }=\log \left(1+\frac{P_1^{\prime }}{\alpha }\right),R_2^{\prime }=\log \left(1+\frac{P_2^{\prime }}{P_1^{\prime }+\beta }\right)\text{\hspace{1em}(6)}$$

当$R_1=R_1^{\prime }$时有

$$\frac{P_1}{P_2+\alpha }=\frac{P_1^{\prime }}{\alpha }\text{\hspace{1em}(7)}$$

进而有

$$\alpha (P_1-P_1^{\prime })=P_2{P}_1^{\prime }\Rightarrow \alpha (P_2^{\prime }-P_2)=P_2{P}_1^{\prime }\text{\hspace{1em}(8)}$$

因为$\alpha >\beta$，所以

$$\beta (P_2^{\prime }-P_2)<P_2{P}_1^{\prime }\text{\hspace{1em}(9)}$$

整理一下，即

$$\frac{P_2}{\beta }>\frac{P_2^{\prime }}{P_1^{\prime }+\beta }\text{\hspace{1em}(10)}$$

故有$R_2>R_2^{\prime }$。

所以证明了当$R_1=R_1^{\prime }$时，必有$R_2>R_2^{\prime }$。显然只有当$P_1=P_1^{\prime }=0$或者$P_2=P_2^{\prime }=0$，等号才成立。

结论

至此，本文从下行容量域的角度解释说明了在非对称的两用户下行NOMA场景，正确的SIC顺序是：

弱用户直接解调数据（即将强用户信号视为干扰），而强用户先解调出弱用户的数据，之后进行干扰消除，最后解调自己的数据。

最后

以上就是勤劳雨为你收集整理的非正交多址(NOMA)下行串行干扰消除(SIC)顺序的分析：从容量域的角度看问题阅读提醒问题背景和系统模型从下行容量域的角度看问题的全部内容，希望文章能够帮你解决非正交多址(NOMA)下行串行干扰消除(SIC)顺序的分析：从容量域的角度看问题阅读提醒问题背景和系统模型从下行容量域的角度看问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。