文章目录
- 1 文本序列表示方法
- 1.1 问题
- 1.2 序列
- 1.3 one-hot编码
- 1.4 Word Vector
- 1.5 Embedding层
- 1.5.1 实现过程
- 1.5.2 TenorFlow中的实现
- 1.6 预训练的词向量
- 2 RNN
- 2.1 问题
- 2.2 全连接层处理文本
- 2.3 共享权值
- 2.4 全局语义
- 2.5 RNN结构
- 2.6 RNN中的梯度传播
- 2.6.1 梯度计算
- 2.6.2 梯度弥散和梯度爆炸
- 2.6.3 梯度裁剪
- 2.7 RNN的主要缺陷
- 3 LSTM
- 3.1 问题
- 3.2 LSTM结构
- 3.2.1 概览
- 3.2.2 遗忘门
- 3.2.3 输入门
- 3.2.4 输出门
- 3.3 LSTM 优缺点
- 4GRU
- 4.1 问题
- 4.2 GRU结构
- 4.2.1 复位门
- 4.2.2 更新门
1 文本序列表示方法
1.1 问题
- 什么是文本序列?
- 怎么把单词转化成文本序列?
1.2 序列
-
概念:具有先后顺序的数据,如随时间变化的商品价格
-
神经网络本质上是一系列的矩阵相乘、相加等运算,并不能够直接处理字符串类型的数据,所以在用神经网络做自然语言处理任务之前,需要把单词或字符转化为数值
1.3 one-hot编码
-
对于英文句子:假设只考虑最常用的 1 万个单词,那么每个单词就可以表示为某位为 1、其他位置为 0 的、长度为 1 万的稀疏one-hot向量,如下图所示:

-
同理,对于中文句子:假设只考虑最常用的 5000 个汉字,则一个汉字可以表示为某位为 1、其他位置为 0 的、长度为 5000 的稀疏one-hot向量
one-hot编码具有如下两大缺点:
-
编码出来的向量过于稀疏,长度很长,加重计算负担;
-
忽略了单词先天具有的语义相关性。如:
- like 和 dislike 均表示情感上喜欢的程度,两个词在语义方面强相关
- Rome 和 Paris 均表示欧洲的城市,同样也是语义强相关
对于这样的单词来说,如果采用 one-hot 编码,得到的向量之间没有相关性,不能体现出原有文字的语义相关性
1.4 Word Vector
语义层面的相关性能够很好地通过 Word Vector 体现出来。
余弦相关度是一种衡量词向量之间相关度的方法 :
s
i
m
i
l
a
r
i
t
y
(
a
,
b
)
=
c
o
s
(
θ
)
=
a
⋅
b
∣
a
∣
⋅
∣
b
∣
similarity(boldsymbol a,boldsymbol b)=cos(theta)=frac{boldsymbol a·boldsymbol b}{|boldsymbol a|·|boldsymbol b|}
similarity(a,b)=cos(θ)=∣a∣⋅∣b∣a⋅b
其中 a 和 b 代表两个词向量。下图表达了单词 France 和 Italy 、ball 和 crocodile 的相似度:
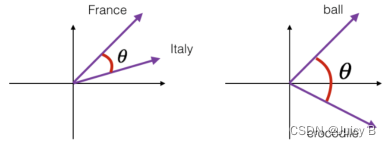
θ 为两个词向量之间的夹角。以 0° 到 180° 为例:
- θ 越大,夹角越大,cos(θ) 越小,两向量之间的相似度越小
- θ 越小,夹角越小,cos(θ) 越大,两向量之间的相似度越大
1.5 Embedding层
1.5.1 实现过程
在神经网络中,单词的表示向量 Word Vector 其实是可以通过训练得到的。实现这种训练行为的表示层叫作 Embedding 层。其实现过程下:
-
将各个单词编号为数字 i ,如 1 表示单词 me,2 表示单词 you;
-
获取词汇表单词数 N ,并记要将单词编码成长度为 n 的向量 ???? ;
-
用下面的函数计算 ????:
???? = f θ ( i ∣ N , n ) ???? = f_theta(i|N,n) v=fθ(i∣N,n) -
用各个单词编码后得到的向量 ???? 构建大小为 [N, n] 的查询表 t ,这样的话,若来了一个新单词(标号为 j ),只需要在 t 的对应位置上查询 ???? 即可:
???? = t [ j ] ????=t[j] v=t[j] -
经过网络训练,得到一个对各个单词都相对合理的编码方式,这样就得到了Embedding层
Embedding 层完成了单词到向量的转换,得到的这些向量可以继续通过神经网络完成后续任务,并计算误差L,采用梯度下降算法来实现端到端的训练,得到文本任务模型。
1.5.2 TenorFlow中的实现
训练Embedding层的过程是一个黑盒,具体使用时调用TensorFlow中的API即可。实现的示例代码如下:
import tensorflow as tf
from tensorflow.keras import layers
x = tf.range(100) # 生成 100 个单词的数字编码
x = tf.random.shuffle(x) # 打散
# 创建共100个单词,每个单词用长度为5的向量表示
# 具体使用时,单词向量长度要根据总单词数的大小进行多次尝试
net = layers.Embedding(100, 5)
# 将输入文本x转化为词向量
out = net(x)
上述代码创建了 100 个单词的 Embedding 层 net,每个单词用长度为 5 的向量表示,这些词向量是随机初始化的,尚未经过网络训练。经过训练后,可以得到更好的表示方法。
训练用到的数据集看下面介绍,
1.6 预训练的词向量
使用预训练的Embedding 模型来训练得到单词的表示方法,往往能得到更好的性能。
用得比较广的预训练模型有如下两种:
- Word2Vec
- GloVe模型 GloVe.6B.50d:词汇量 40 万,每个单词使用长度为 50 的向量表示,用户只需要下载对应的模型文件 “glove6b50dtxt.zip” 就可使用
有了预训练的词向量模型,就可以用来初始化 Embedding 层的查询表,从而代替了随机初始化,得到更好的词向量表示方法。代码如下:
# 从预训练模型中加载词向量表
glove = load_embed('glove.6B.50d.txt')
# 利用预训练的词向量表初始化Embedding层
net.set_weights([glove])
这样得到的Embedding层不用经过训练,直接用”前人的智慧“,就得到了较好的、通用的Embedding层。
2 RNN
2.1 问题
-
对比全连接层,用RNN处理文本有什么优势?
-
RNN的基本原理是什么?
-
如何在全连接层的基础上做一步步改进得到RNN?
2.2 全连接层处理文本
使用全连接层处理文本分类任务的思路如下:
-
对于每个词向量,分别使用一个全连接层网络提取语义特征:
Font metrics not found for font: . -
将提取到的所有单词的特征进行合并,得到2分类的概率分布。
示意图如下:
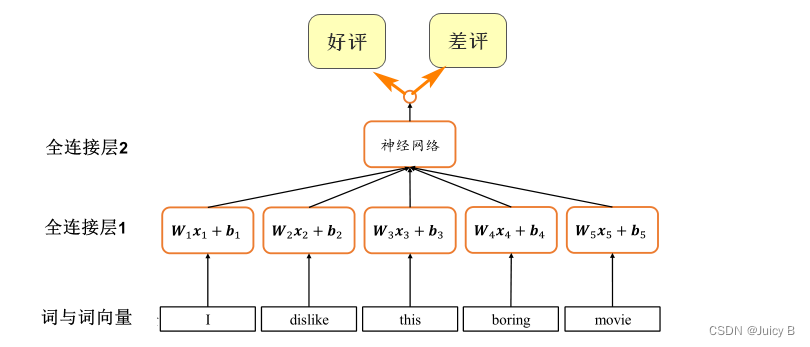
这种方法简单粗暴,有很大的缺陷:
- 每个单词都要配一个全连接层子网络,导致网络参数量太大,内存占用和计算代价高
- 由于不同文本长度不同,使得每个序列的长度并不相同,导致网络结构要一直改变,导致训练过程中网络结构低效、不稳定
- 每个全连接层子网络的参数 Wt 和 bt 只能感受当前词向量的输入,而无法感知之前和之后的语境信息,导致句子整体语义的缺失
为了解决这些缺陷,下面提出了几个新的概念。
2.3 共享权值
共享权值的思想在卷积神经网络中有着很显著的体现。
卷积神经网络之所以在处理局部相关数据时的效果优于全连接网络,是因为它充分利用了权值共享的思想。
以处理图像为例,对于图像中的每一层都使用同一个参数、尺寸一致的卷积核提取特征,进而大大减少了网络的参数量。
参照这一思想,我们可以将上述全连接层处理文本的过程改为如下形式:
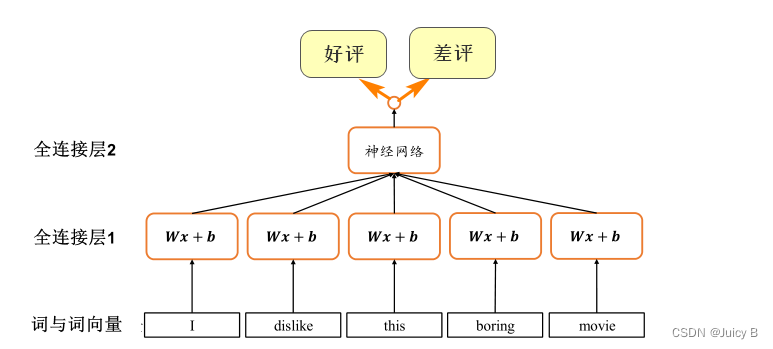
使用共享权值之后可以得到如下好处:
- 参数量大大减少
- 网络训练更加稳定高效
解决了前两点,但下面这一点还是无法解决:
- 没有考虑序列之间的先后顺序,无法获取全局语义信息
为了解决这个缺点,又提出了”全局语义“的概念。
2.4 全局语义
上面两个结构均无法提取全局语义信息。为了提取全局语义,一个可行的思路如下:
- 提供一个单独的内存变量,每次提取一个词向量的特征后,刷新内存变量
- 将该内存变量作为参数送到下一个词向量的特征提取当中,如此递归进行,直至输入最后一个词向量的特征提取为止
- 经过上述过程的内存变量即存储了所有序列的语义特征,并且由于输入序列之间的先后顺序,使得内存变量内容与序列顺序紧密关联。
上述思路的示意图如下:
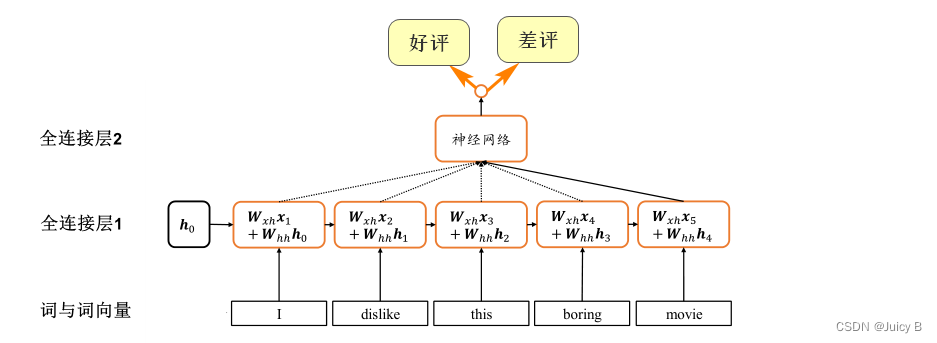
各参数的含义为:
- h t boldsymbol {h_t} ht:上面提到的”内存变量“,也叫状态张量
- t t t :时间戳标记
- W x h boldsymbol {W_{xh}} Wxh:共享的权值,用于提取词向量的特征
- W h h boldsymbol {W_{hh}} Whh:共享的权值,用于提取上一个时间戳的状态张量的特征
- b boldsymbol b b : 偏置项
每个时间戳上状态张量
h
t
h_t
ht的更新公式为:
h
t
=
σ
(
W
x
h
x
t
+
W
h
h
h
t
−
1
+
b
)
boldsymbol {h_t}=sigma(boldsymbol {W_{xh}}boldsymbol x_t +boldsymbol {W_{hh}}boldsymbol {h_{t-1}}+boldsymbol b)
ht=σ(Wxhxt+Whhht−1+b)
经过这样的运算,最后一个时间戳上的
h
t
boldsymbol {h_t}
ht就较好地代表了句子的全局语义信息,并且句子中不同时间戳上的单词也被串联了起来。
2.5 RNN结构
在上面的基础上,得到一种新的结构如下:
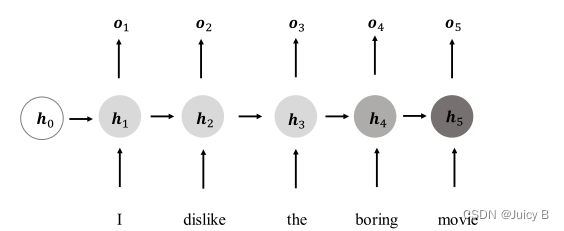
上图各参数的含义如下:
在每个时间戳 t 上,网络层接受如下两个参数:
- 当前时间戳 t t t 的输入 x t boldsymbol {x_{t}} xt;
- 上一个时间戳的网络状态向量 h t − 1 boldsymbol {h_{t-1}} ht−1.
经过下面公式计算后,得到当前时间戳的状态向量
h
t
boldsymbol {h_{t}}
ht:
h
t
=
f
θ
(
h
t
−
1
,
x
t
)
boldsymbol {h_{t}}=f_theta(boldsymbol {h_{t-1}},boldsymbol {x_{t}})
ht=fθ(ht−1,xt)
其中,
f
θ
f_theta
fθ代表网络的运算逻辑,θ 为网络参数。
在每个时间戳上,将网络的状态向量变换后输出:
o
t
=
g
ϕ
(
h
t
)
boldsymbol o_{t}=g_phi(boldsymbol h_{t})
ot=gϕ(ht)
将上图表示成在时间轴上进行折叠的形式,如下图所示:
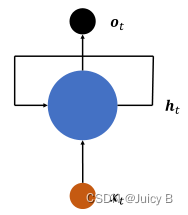
这种结构就称为 循环网络结构(RNN结构)。
RNN结构包含了如下几项工作:
-
接受文本序列中每个单词的每个特征向量 x t boldsymbol {x_{t}} xt
-
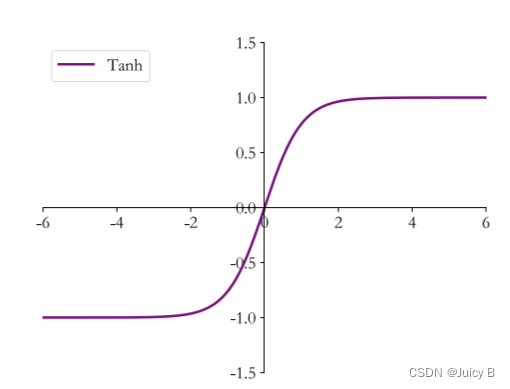
刷新内部状态向量 h t boldsymbol {h_{t}} ht,计算公式为:
h t = σ ( W x h x t + W h h h t − 1 + b ) boldsymbol h_t=sigma(boldsymbol W_{xh}boldsymbol x_t +boldsymbol W_{hh}boldsymbol h_{t-1}+boldsymbol b) ht=σ(Wxhxt+Whhht−1+b)
其中, σ sigma σ为激活函数,在 RNN 中多用 tanh 函数:
-
由 h t boldsymbol {h_{t}} ht得到输出 o t boldsymbol {o_{t}} ot,有两种方式:
-
状态向量 h t boldsymbol {h_{t}} ht直接用作输出 :
o t = h t boldsymbol o_{t}=boldsymbol h_{t} ot=ht -
对 h t boldsymbol {h_{t}} ht做一个简单的线性变换后再得到输出:
o t = W h o h t boldsymbol o_{t}=boldsymbol W_{ho} boldsymbol h_{t} ot=Whoht
-
2.6 RNN中的梯度传播
2.6.1 梯度计算
下面来推导一下 RNN 结构中的梯度传播,观察特点,并发现其中隐藏的问题。
设 L 为网络的误差,则由链式求导法则可得 L 对共享权值的偏导如下:
∂
L
∂
W
h
h
=
∑
i
=
1
t
∂
L
∂
o
t
∂
o
t
∂
h
t
∂
h
t
∂
h
i
∂
h
i
∂
W
h
h
frac{partial L}{partial boldsymbol W_{hh}}=sum_{i=1}^t frac{partial L}{partial boldsymbol o_{t}} frac{partial boldsymbol o_{t}}{partial boldsymbol h_{t}} frac{partial boldsymbol h_{t}}{partial boldsymbol h_{i}} frac{partial boldsymbol h_{i}}{partial boldsymbol W_{hh}}
∂Whh∂L=i=1∑t∂ot∂L∂ht∂ot∂hi∂ht∂Whh∂hi
其中:
-
∂ L ∂ o t frac{partial L}{partial boldsymbol o_{t}} ∂ot∂L可由损失函数直接求得,视不同情况而定
-
∂ o t ∂ h t frac{partial boldsymbol o_{t}}{partial boldsymbol h_{t}} ∂ht∂ot的值为:
∂ o t ∂ h t = { 1 , o t = h t W h o , o t = W h o h t frac{partial boldsymbol o_{t}}{partial boldsymbol h_{t}}= left{begin{array}{l}1,qquad boldsymbol o_{t}=boldsymbol h_{t} \ boldsymbol W_{ho},quad boldsymbol o_{t}=boldsymbol W_{ho} boldsymbol h_{t} end{array}right. ∂ht∂ot={1,ot=htWho,ot=Whoht -
∂ h i ∂ W h h frac{partial boldsymbol h_{i}}{partial boldsymbol W_{hh}} ∂Whh∂hi的求解公式为:
∂ h i ∂ W h h = ∂ σ ( W x h x i + W h h h i − 1 + b ) ∂ W h h frac{partial boldsymbol h_{i}}{partial boldsymbol W_{hh}}=frac {partial sigma(boldsymbol W_{xh}boldsymbol x_i +boldsymbol W_{hh}boldsymbol h_{i-1}+boldsymbol b)} {partial boldsymbol W_{hh}} ∂Whh∂hi=∂Whh∂σ(Wxhxi+Whhhi−1+b) -
∂ h t ∂ h i frac{partial boldsymbol h_{t}}{partial boldsymbol h_{i}} ∂hi∂ht的求解过程如下:
∂ h t ∂ h i = ∂ h t ∂ h t − 1 ∂ h t − 1 ∂ h t − 2 ⋅ ⋅ ⋅ ∂ h i + 1 ∂ h i = ∏ k = 1 t − 1 ∂ h k + 1 ∂ h k frac{partial boldsymbol h_{t}}{partial boldsymbol h_{i}}= frac{partial boldsymbol h_{t}}{partial boldsymbol h_{t-1}} frac{partial boldsymbol h_{t-1}}{partial boldsymbol h_{t-2}} ··· frac{partial boldsymbol h_{i+1}}{partial boldsymbol h_{i}} = prod_{k=1}^{t-1} frac{partial boldsymbol h_{k+1}}{partial boldsymbol h_{k}} ∂hi∂ht=∂ht−1∂ht∂ht−2∂ht−1⋅⋅⋅∂hi∂hi+1=k=1∏t−1∂hk∂hk+1
又:
h k + 1 = σ ( W x h x k + 1 + W h h h k + b ) boldsymbol h_{k+1}=sigma(boldsymbol W_{xh}boldsymbol x_{k+1} +boldsymbol W_{hh}boldsymbol h_{k}+boldsymbol b) hk+1=σ(Wxhxk+1+Whhhk+b)
故:
∂ h k + 1 ∂ h k = d i a g ( σ ′ ( W x h x k + 1 + W h h h k + b ) ) W h h frac{partial boldsymbol h_{k+1}}{partial boldsymbol h_{k}}= diag(sigma^{'}(boldsymbol W_{xh}boldsymbol x_{k+1} +boldsymbol W_{hh}boldsymbol h_{k}+boldsymbol b))boldsymbol W_{hh} ∂hk∂hk+1=diag(σ′(Wxhxk+1+Whhhk+b))Whh
所以:
∂ h t ∂ h i = ∏ k = 1 t − 1 d i a g ( σ ′ ( W x h x k + 1 + W h h h k + b ) ) W h h frac{partial boldsymbol h_{t}}{partial boldsymbol h_{i}}= prod_{k=1}^{t-1} diag(sigma^{'}(boldsymbol W_{xh}boldsymbol x_{k+1} +boldsymbol W_{hh}boldsymbol h_{k}+boldsymbol b))boldsymbol W_{hh} ∂hi∂ht=k=1∏t−1diag(σ′(Wxhxk+1+Whhhk+b))Whh
经过上述运算,最终就可以求得 ∂ h i ∂ W h h frac{partial boldsymbol h_{i}}{partial boldsymbol W_{hh}} ∂Whh∂hi的梯度。
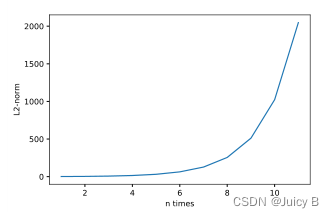
从上述公式可以看到, ∂ h t ∂ h i frac{partial boldsymbol h_{t}}{partial boldsymbol h_{i}} ∂hi∂ht这一梯度计算包含了非常多的累乘项,导致RNN的训练非常困难。
2.6.2 梯度弥散和梯度爆炸
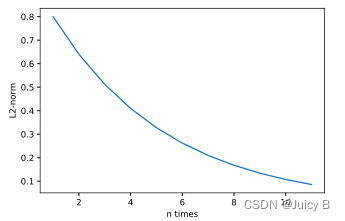
∂ h t ∂ h i frac{partial boldsymbol h_{t}}{partial boldsymbol h_{i}} ∂hi∂ht包含了 W h h boldsymbol W_{hh} Whh的连乘运算,这会出现下面的情况:
-
当 W h h boldsymbol W_{hh} Whh的最大特征值小于1时,多次连乘运算会使得 ∂ h t ∂ h i frac{partial boldsymbol h_{t}}{partial boldsymbol h_{i}} ∂hi∂ht的值接近于零。
这一现象叫做 梯度弥散:
-
当 W h h boldsymbol W_{hh} Whh的最大特征值大于1时,多次连乘运算会使得 ∂ h t ∂ h i frac{partial boldsymbol h_{t}}{partial boldsymbol h_{i}} ∂hi∂ht的值非常大。
这一现象叫做 梯度爆炸:
出现这两种情况时,网络训练起来会非常困难。数学解释如下。
梯度下降算法的公式为:
θ
′
=
θ
−
η
▽
θ
L
theta^{'}=theta-etabigtriangledown_theta L
θ′=θ−η▽θL
出现梯度弥散现象时:
▽ θ L bigtriangledown_theta L ▽θL≈ 0 ,导致 θ ′ = θ theta^{'}=theta θ′=θ,也就是说每次梯度更新后参数基本保持不变,神经网络的参数长时间得不到更新, L L L 也基本保持不变,导致无法收敛。
出现梯度爆炸现象时:
▽ θ L bigtriangledown_theta L ▽θL远远大于 1 ,导致梯度更新的步长 η ▽ θ L etabigtriangledown_theta L η▽θL很大, θ ′ theta^{'} θ′与 θ theta θ的差距过大, L L L会出现突变、来回震荡的现象,也导致无法收敛。
如何解决这两个问题?
对于梯度弥散现象,可用的解决方法有:
- 增大学习率
- 减少网络深度
- 使用深度残差网络
对于梯度爆炸现象,主要用到梯度裁剪的方法。
2.6.3 梯度裁剪
梯度裁剪的主要思想为:
将梯度张量的数值或者范数限制在某个较小的区间内,使得远大于1的梯度值减少,避免出现梯度爆炸。
梯度裁剪的方法主要有如下三种。
-
直接对张量的数值进行限幅,使得张量 ???? 的所有元素????ij 都落在区间 [min,max] 中。
使用 TensorFlow 实现该方法的示例代码如下:
import tensorflow as tf # 生成随机数 a = tf.random.uniform([3,3]) # 梯度值裁剪 tf.clip_by_value(a,0.3,0.5)输出为:
<tf.Tensor: shape=(3, 3), dtype=float32, numpy=
array([[0.5 , 0.3 , 0.49528742],
[0.5 , 0.5 , 0.5 ],
[0.36500812, 0.5 , 0.5 ]], dtype=float32)> -
对张量 ???? 的范数进行限幅,使得 ???? 的二范数被约束在区间 [0,max] 中。
使用 TensorFlow 实现该方法的示例代码如下:
import tensorflow as tf a = tf.random.uniform([3,3]) * 10 # 按范数方式裁剪 b = tf.clip_by_norm(a, 10) # 裁剪前和裁剪后的张量范数 print("裁剪前:", float(tf.norm(a))) print("裁剪后:", float(tf.norm(b)))输出为:
裁剪前: 15.314314842224121
裁剪后: 10.0可以看到,对于大于max = 10 的 L2 范数的张量,裁剪后的范数缩减为 10。
-
前两种方法只是简单地对梯度张量进行限幅,这可能会导致网络更新方向发生变动的情况发生,使得网络不稳定。而 全局范数裁剪 则考虑了所有参数的梯度????的范数,实现等比例的缩放。这样的好处为:
-
既很好地限制网络的梯度值
-
又不改变网络的更新方向
全局范数的计算公式如下:
g l o b a l _ n o r m = ∑ i ∣ ∣ W ( i ) ∣ ∣ 2 2 global_norm =sqrt {{sum_i}||boldsymbol W^{(i)}||_2^2 } global_norm=i∑∣∣W(i)∣∣22
其中, W ( i ) boldsymbol W^{(i)} W(i)表示第 i i i个梯度张量。得到全局范数之后,全局范数裁剪的公式如下:
???? ( i ) = ???? ( i ) ⋅ m a x _ n o r m m a x ( g l o b a l _ n o r m , m a x _ n o r m ) ???? ^{(i)} = frac{???? ^{(i)}·max_norm}{max(global_norm,max_norm)} W(i)=max(global_norm,max_norm)W(i)⋅max_norm
其中,max_norm 为全局最大范数值,由用户自己指定。使用 TensorFlow 实现该方法的示例代码如下:
import tensorflow as tf # 创建第一个梯度张量 w1 = tf.random.normal([3,3]) # 创建第二个梯度张量 w2 = tf.random.normal([3,3]) # 计算全局范数 global_norm = tf.math.sqrt(tf.norm(w1)**2 + tf.norm(w2)**2) # 设置max_norm=2,进行裁剪 (ww1,ww2), global_norm = tf.clip_by_global_norm([w1,w2],2) # 计算裁剪后的张量组的 global norm global_norm2 = tf.math.sqrt(tf.norm(ww1)**2+tf.norm(ww2)**2) # 打印裁剪前的全局范数和裁剪后的全局范数 print("裁剪前的全局范数:%.5f" % global_norm) print("裁剪后的全局范数:%.5f" % global_norm2)输出为:
裁剪前的全局范数:4.02665
裁剪后的全局范数:2.00000裁剪前的张量 w1 为:
<tf.Tensor: shape=(3, 3), dtype=float32, numpy=
array([[-2.267207 , 1.2793622 , -0.22873628],
[-0.08037159, 0.39103642, -1.0350872 ],
[ 0.99171644, 0.45965433, -0.5615316 ]], dtype=float32)>裁剪后的张量 ww1 为:
<tf.Tensor: shape=(3, 3), dtype=float32, numpy=
array([[-1.1261013 , 0.6354477 , -0.11361125],
[-0.03991984, 0.19422427, -0.5141185 ],
[ 0.49257663, 0.22830616, -0.2789077 ]], dtype=float32)> -
在TensorFlow使用梯度裁剪方法的通用代码如下(这里用到的是全局梯度裁剪方法,其他两种方法的使用方式也是一样的):
# 下面代码中,model为自定义的模型,y为数据集的标签,tape为梯度记录器
with tf.GradientTape() as tape:
# 前向传播
logits = model(x)
# 使用交叉熵损失做误差函数,计算误差
loss = criteon(y, logits)
# 计算梯度值
grads = tape.gradient(loss, model.trainable_variables)
# 得到梯度值之后,进行全局梯度裁剪,n是一个整数,视具体情况而定
grads_clipped, _ = tf.clip_by_global_norm(grads, n)
# 利用裁剪后的梯度张量更新参数
optimizer.apply_gradients(zip(grads_clipped, model.trainable_variables))
2.7 RNN的主要缺陷
经过上面的分析,可以总结出 RNN 的第一个主要缺陷:
- 容易出现梯度弥散或梯度爆炸的现象。
还有另一个致命的缺陷:
-
RNN 的记忆是一种短时记忆,意思是说,RNN 在处理较长的句子时,往往只能够理解有限长度内的信息,而对于位于较长范围类的信息却不能够很好地串联起来。例如这句话:
“今天是阴天,空气很凉爽,虽然没有太阳天空看起来灰蒙蒙的,但丝毫不能减弱人们的愉悦感。”
为了延长这种短时记忆,科学家提出了 长短时记忆网络 Long Short-Term Memory,简称 LSTM。LSTM 相比基础 RNN 网络具有如下优点:
- 记忆能力更强
- 更擅长处理较长的序列
下面就来介绍 LSTM。
3 LSTM
3.1 问题
- 为了解决RNN的主要缺陷,LSTM做出了什么改变?
- LSTM原理是什么,它是怎么工作的?
3.2 LSTM结构
3.2.1 概览
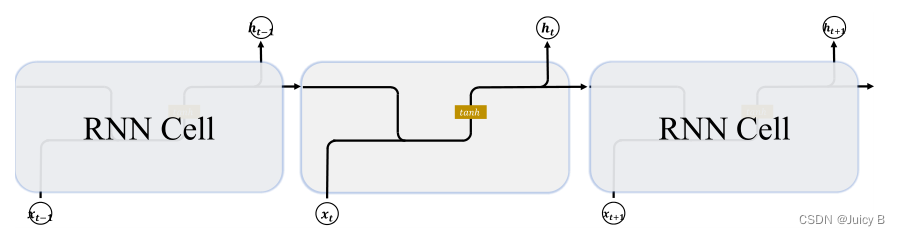
基础 RNN 结构的示意图如下所示:
LSTM 结构的示意图如下:
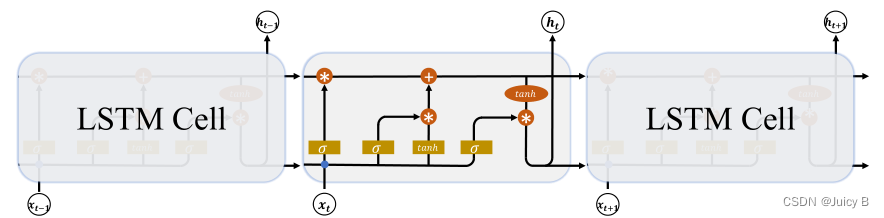
LSTM 中,有两个状态向量:
- 状态向量 c
- 状态向量 h
LSTM 主要运用门控机制来控制信息流动。门控机制类似于“开闸放水”,其大概原理如下:
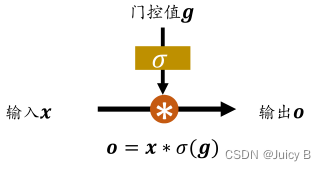
图中,g 表示水阀门打开的程度,σ(g) 将 g 的值压缩到区间 [0, 1] 当中,x 表示输入的水流,
o 表示出阀门的水流
- σ(g) = 1 时,阀门全部打开,水流量o = x,达到最大
- σ(g) = 0 时,阀门全部打开,水流量o = 0,最小
LSTM 用到了如下三种门控:
- 遗忘门
- 输入门
- 输出门
3.2.2 遗忘门
遗忘门用于控制上一个时间戳
t
−
1
t-1
t−1 的输出
c
t
−
1
boldsymbol {c_{t-1}}
ct−1对当前时间戳的影响。示意图如下:
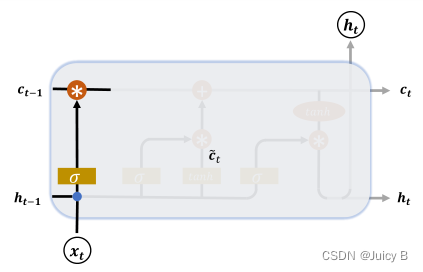
遗忘门门控变量的计算公式为:
g
f
=
σ
(
W
f
[
h
t
−
1
,
x
t
]
+
b
f
)
boldsymbol g_f = sigma(boldsymbol W_f[boldsymbol h_{t-1},boldsymbol x_t]+boldsymbol b_f)
gf=σ(Wf[ht−1,xt]+bf)
其中:
-
W f bold W_f Wf 和 b f bold b_f bf可由反向传播算法自动优化
-
σ sigma σ 为激活函数,在遗忘门里多用 sigmoid 函数
从示意图中可以看到,经过遗忘门后,LSTM 的状态向量为:
g f c t − 1 boldsymbol g_fboldsymbol c_{t-1} gfct−1 -
g f bold g_f gf = 1 时,遗忘门全部打开,LSTM接受上一个状态向量 c t − 1 bold c_{t-1} ct−1的所有信息
-
g f bold g_f gf = 0 时,遗忘门全部关闭,LSTM直接忽略一个状态向量 c t − 1 bold c_{t-1} ct−1,输出 0 向量
3.2.3 输入门
输入门用于控制 LSTM 对输入 x t bold x_t xt的接收程度。示意图如下:
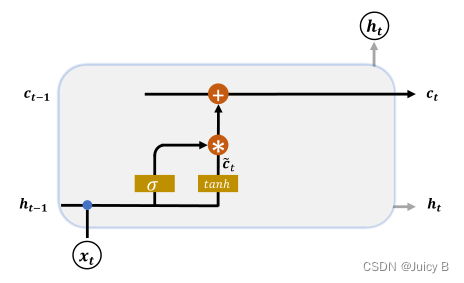
计算步骤如下:
-
对当前时间戳的输入 x t bold x_t xt 和上一个时间戳的输出 c t − 1 bold c_{t-1} ct−1 做非线性变换得到新的输入向量:
c ~ t = t a n h ( W c [ h t − 1 , x t ] + b c ) widetilde{boldsymbol c}_t=tanh(boldsymbol W_c[boldsymbol h_{t-1},boldsymbol x_t] + boldsymbol b_c) c t=tanh(Wc[ht−1,xt]+bc)
其中:- W c bold W_c Wc 和 b c b_c bc 为输入门参数,通过反向传播算法自动优化
- tanh 为激活函数
-
求出门控变量:
g i = σ ( W i [ h t − 1 , x t ] + b i ) {boldsymbol g}_i=sigma(boldsymbol W_i[boldsymbol h_{t-1},boldsymbol x_t] + boldsymbol b_i) gi=σ(Wi[ht−1,xt]+bi)
其中:- W i bold W_i Wi和 b i bold b_i bi 为输入门参数,通过反向传播算法自动优化
- σ 为 sigmoid 激活函数
-
用门控变量对 c ~ t widetilde{boldsymbol c}_t c t进行约束:
g i c ~ t {boldsymbol g}_i widetilde{boldsymbol c}_t gic t- g i bold g_i gi = 1 时,LSTM 接受全部的新输入向量 c ~ t widetilde{boldsymbol c}_t c t
- g i bold g_i gi = 0 时,LSTM 直接忽略新输入向量 c ~ t widetilde{boldsymbol c}_t c t
在遗忘门和输入门的控制下,状态向量
c
t
c_t
ct 的刷新方式为:
c
t
=
g
f
c
t
−
1
+
g
i
c
~
t
boldsymbol c_t=boldsymbol g_fboldsymbol c_{t-1}+{boldsymbol g}_i widetilde{boldsymbol c}_t
ct=gfct−1+gic
t
3.2.4 输出门
LSTM 的内部状态向量 $$ 并不会直接用于输出,而是在输出门的作用下有选择性地输出。
输出门的示意图如下:
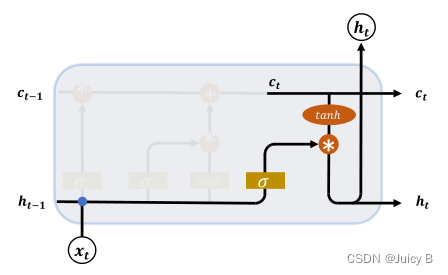
输出门门控变量的计算公式为:
g
o
=
σ
(
W
o
[
h
t
−
1
,
x
t
]
+
b
o
)
{boldsymbol g}_o=sigma(boldsymbol W_o[boldsymbol h_{t-1},boldsymbol x_t] + boldsymbol b_o)
go=σ(Wo[ht−1,xt]+bo)
LSTM 的输出为:
h
t
=
g
o
⋅
t
a
n
h
(
c
t
)
{boldsymbol h}_t=boldsymbol g_o·tanh(boldsymbol c_t)
ht=go⋅tanh(ct)
- g o = 1 g_o= 1 go=1 时,输出门全部打开,LSTM的状态向量 c t c_t ct 全部用于输出
- g o = 0 g_o= 0 go=0 时,输出门全部关闭,输出中不包含 c t c_t ct
| 输入门 | 遗忘门 | 功能 |
|---|---|---|
| 0 | 0 | 清除记忆 |
| 0 | 1 | 只使用记忆 |
| 1 | 0 | 输入覆盖掉记忆 |
| 1 | 1 | 使用输入和记忆 |
3.3 LSTM 优缺点
优点:
- 性能比基础 RNN 好,不容易出现梯度弥散
- 记忆能力比基础 RNN 好
缺点:
- 结构较复杂,参数量大,计算代价高
为了解决这一问题,提出了 GRU 结构。
4GRU
4.1 问题
- 为了解决LSTM的主要缺陷,GRU做出了什么改变?
- GRU的结构长什么样,工作原理是什么?
4.2 GRU结构
GRU 的主要设计思路为:把内部状态向量和输出向量合并,并减少门控数量。
其结构示意图如下:
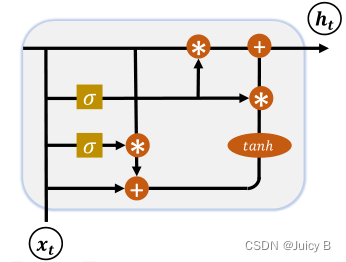
GRU 的门控减少为两个:更新门和复位门。
4.2.1 复位门
复位门用于控制上一个时间戳的状态向量进入 GRU 结构的量。示意图如下:
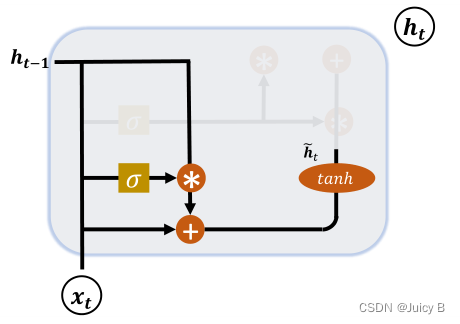
门控变量的计算公式如下:
g
r
=
σ
(
W
r
[
h
t
−
1
,
x
t
]
+
b
r
)
{boldsymbol g}_r=sigma(boldsymbol W_r[boldsymbol h_{t-1},boldsymbol x_t] + boldsymbol b_r)
gr=σ(Wr[ht−1,xt]+br)
h ~ t = t a n h ( W h [ g r h t − 1 , x t ] + b c ) widetilde{boldsymbol h}_t=tanh(boldsymbol W_h[boldsymbol g_{r}boldsymbol h_{t-1},boldsymbol x_t] + boldsymbol b_c) h t=tanh(Wh[grht−1,xt]+bc)
- gr = 1 时, h t − 1 boldsymbol h_{t-1} ht−1共同生成新输入 h ~ t widetilde{boldsymbol h}_t h t;
- gr = 0 时, h ~ t widetilde{boldsymbol h}_t h t全部由 x t boldsymbol x_t xt产生,忽略了 h t − 1 boldsymbol h_{t-1} ht−1,相当于复位 h t − 1 boldsymbol h_{t-1} ht−1
4.2.2 更新门
更新门用控制上一时间戳的状态向量 h t − 1 boldsymbol h_{t-1} ht−1和新输入 h ~ t widetilde{boldsymbol h}_t h t对新状态向量 h t {boldsymbol h}_t ht的影响程度。
示意图如下:
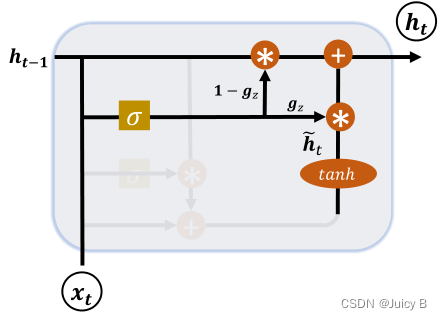
门控变量的计算公式如下:
g
z
=
σ
(
W
z
[
h
t
−
1
,
x
t
]
+
b
z
)
{boldsymbol g}_z=sigma(boldsymbol W_z[boldsymbol h_{t-1},boldsymbol x_t] + boldsymbol b_z)
gz=σ(Wz[ht−1,xt]+bz)
新状态向量
h
t
{boldsymbol h}_t
ht的计算公式为:
h
t
=
(
1
−
g
z
)
h
t
−
1
+
g
z
h
~
t
{boldsymbol h}_t=(1-boldsymbol g_z)boldsymbol h_{t-1}+ boldsymbol g_z widetilde {boldsymbol h}_t
ht=(1−gz)ht−1+gzh
t
可见,
1
−
g
z
1-boldsymbol g_z
1−gz用于控制
h
t
−
1
{boldsymbol h}_{t-1}
ht−1
- g z = 0 boldsymbol g_z= 0 gz=0 时, h t boldsymbol h_t ht全部来自 h t − 1 boldsymbol h_{t-1} ht−1
- g z = 1 boldsymbol g_z= 1 gz=1时, h t boldsymbol h_t ht全部来自 h ~ t widetilde {boldsymbol h}_t h t
最后
以上就是飘逸鱼最近收集整理的关于【循环神经网络介绍】文本序列表示方法、RNN、LSTM和GRU原理1 文本序列表示方法2 RNN3 LSTM4GRU的全部内容,更多相关【循环神经网络介绍】文本序列表示方法、RNN、LSTM和GRU原理1内容请搜索靠谱客的其他文章。








发表评论 取消回复