提要
运用频率响应法,进一步讨论系统的稳定性。结合伯德图和奈奎斯特图,介绍增益裕度、相角裕度和带宽等的概念,研究频域内的稳定性判别方法——奈奎斯特稳定性判据。讨论时间延迟环节对控制系统稳定性和性能指标的影响(引入了附加的滞后相角,因而有可能导致条件稳定系统失稳)
收获
(1)掌握奈奎斯特稳定性判据和奈奎斯特图的作用;
(2)熟悉系统时域性能的频域表示方法;
(3)理解在反馈控制系统设计中,考虑时间延迟环节的重要性;
(4)能够使用频率响应法分析反馈控制系统的相对稳定性和性能,包括系统的增益裕度、相角裕度和带宽等;
(5)理解频域的性能指标,以及用增益裕度和相角裕度表示的系统的相对稳定性。
一. 基本概念
- 再次讨系统的稳定性
分析一个控制系统时,首先看它地稳定性。如果系统稳定,还应该考察它的相对稳定性。
前述关于稳定性的判定:劳斯-赫尔维茨判据基于特征方程判断系统的稳定性;
前述关于系统相对稳定性的方法:根轨迹
这两种方法都是基于复变量
2. 奈奎斯特稳定性判据
奈奎斯特稳定性判据是研究线性系统(齐次性、叠加性)相对稳定的基本方法,它的理论基础是复变函数中柯西(Cauchy)定理。
3. 围线映射
在频域稳定性中关心的是由函数 F(s) 诱导的围线映射,它是指,利用关系函数 F(s) ,将一个复平面上的闭合曲线或轨迹映射转换到另一个平面。例如当 F(s) = 2s+1 时,函数 F(s) 将 s平面上的闭合曲线映射到了 F(s) 平面上,于是有
典型的映射函数 F(s) 都是有理函数。
4. 保角映射
s 平面的围线映射到 F(s) 平面之后,围线上的角度保持不变,这种映射称之为保角映射。
5. 柯西定理/相角原理
如果闭合曲线
6. 奈奎斯特稳定性判据表述1
当
7. 奈奎斯特稳定性判据表述2
闭环反馈控制系统稳定的充要条件是:
8. 基本判定的思路小结
研究闭环控制系统的相对稳定性,考察闭环系统的特征方程为
则应用柯西定理,可以判断 F(s) 不稳定的零点个数为
而又考虑到
二. 基本知识回顾
- 相对稳定性
在 s 平面上,使用劳斯稳定性判据判定系统的稳定性,用每个或者每对闭环特征根的相对调节时间(或衰减因子、或实部绝对值)来衡量系统的相对稳定性;系统的调节时间越短,相对稳定性就越好;
使用频率响应法时,奈奎斯特稳定性判据所提供的信息既能用于判断闭环系统的绝对稳定性,也能用于定义和评价系统的相对稳定性。即在奈奎斯特稳定性判据中,关注的焦点是开环传递函数(
指标一:增益裕度:
当
揭示的内涵是:在系统达到临界稳定之前,系统增益容许的放大倍数。系统到达临界稳定时,奈奎斯特图将在相角为
指标一:相角裕度:
定义:为了使极坐标曲线的单位幅值点(
揭示的内涵是:在系统达到临界稳定之前,L(jw) 的单位幅值点所允许的相移量。系统到达临界稳定时,奈奎斯特图将在相角为
2. 相对稳定性的表示
与极坐标曲线相比较,更愿意使用开环伯德图,并且利用伯德图也可以方便地得到增益裕度和相角裕度
在伯德图上,根据幅频特性曲线与 0 dB增益线的交点,就可以在相频特性曲线的对应频率点上,估计得到系统的相位裕度;观察相频特性曲线与
尽管增益裕度和相角裕度同样是系统的性能指标,但我们通常更多的使用相角裕度。
3. 最小相位系统和非最小相位系统判定的区别
当系统为最小相位系统(系统的零点全部在左半平面)时,可以简单地直接考察奈奎斯特图(极坐标曲线)来判定系统的翁定性指标;可以用计算机程序直接估算增益裕度和相角裕度。
而当系统为非最小相位系统时,就必须谨慎小心一些,只有考察完整的奈奎斯特图,才能确定系统的稳定性指标
4. 看度说话
通过伯德图,当幅值增益为 0 dB 时,对应的相角为
5. 频域响应和时域响应的联系
对于一个二阶系统,建立欠阻尼系统的相角裕度与阻尼系数
另一频域指标,闭环频率响应的最大幅值
怎么做呢?
在单位负反馈的情况下,利用闭环频率响应的等幅值圆,可以在幅相图中确定
判定方法为:
得到系统的闭环频率响应,如果只需要确定
等M圆和等N圆适用于在极坐标平面上分析和设计控制系统,由于更容易得到系统的开环伯德图或对数幅相图,我们更愿意将等M圆和等N圆转换为对数幅值的形式,这称为尼克尔斯图。
6. 系统带宽
闭环控制系统的带宽是度量系统的信号复现能力的最好参数。定义是对低频段增益为 0dB的系统,其带宽定义为幅值增益下降至-3 dB 时对应的频率。在通常情况下,它与阶跃响应速度成正比,与调节时间成反比。因此,在保证系统合理构成的前提下,我们总是希望系统具有较大的带宽。
7. 时延系统的稳定性
时延环节会影响反馈系统的稳定性,幸运的是,可以用奈奎斯特稳定性判据来确定延时环节对反馈系统稳定性的影响。它的传递函数表示为
取舍:由于实际的反馈系统难免含有时延环节,因此为了确保系统稳定,必须减小系统增益,但是减小增益将会增大系统的稳态误差。因此在增强实验系统的稳定性的同时,付出了增大稳态误差的代价。
8. 帕德近似
帕德近似,指定一个给定阶次的待定有理函数来近似
对比麦克劳林级数
和
对比系数可以得到
令
三. matlab指令计算
使用的函数有nyquist,nichols,pade,ngrid,margin
- 使用nyquist绘制奈奎斯特曲线
前向通道的传递函数为
% The nyquist function with manual scaling using the
% axis function. The transfer function is
%
% 0.5
% G(s) = ---------------------------
% s^3 + 2 s^2 + s + 0.5
%
num=[0.5]; den=[1 2 1 0.5 ];
sys=tf(num,den);
nyquist(sys);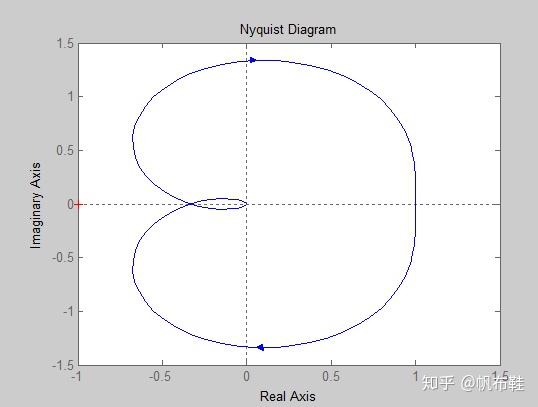
2. 使用margin函数绘制伯德图,并标注增益裕度和相角裕度
% The margin function. The transfer function is
%
% 0.5
% G(s) = ---------------------------
% s^3 + 2 s^2 + s + 0.5
%
num=[0.5]; den=[1 2 1 0.5];
sys=tf(num,den);
margin(sys);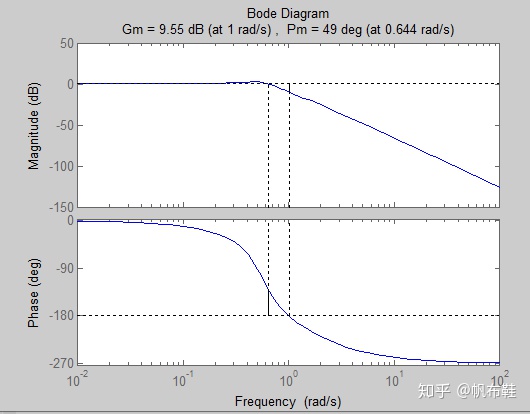
3. 结合1.2,绘制奈奎斯特曲线并标注增益裕度和相角裕度
% The Nyquist plot of
%
% 0.5
% G(s) = ---------------------------
% s^3 + 2 s^2 + s + 0.5
%
% with gain and phase margin calculation.
%
num=[0.5]; den=[1 2 1 0.5 ]; sys=tf(num,den);
%
[mag,phase,w]=bode(sys);
[Gm,Pm,Wcg,Wcp]=margin(mag,phase,w);
%
nyquist(sys);
title(['Gm = ',num2str(Gm),' Pm = ',num2str(Pm)])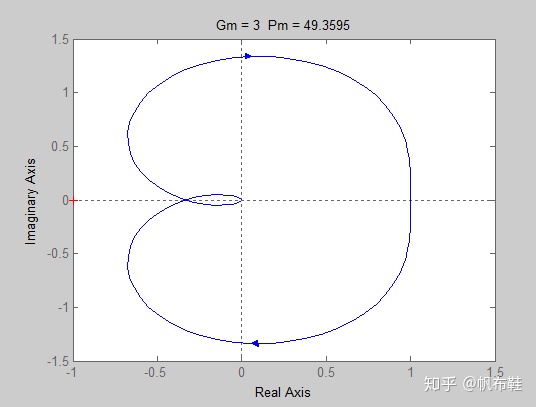
4. 使用nichols来绘制尼克尔斯图
ngrid可以在尼克尔图中绘制网格坐标
% The Nichols chart of
%
% 1
% G(s) = ------------------------- .
% 0.2 s^3 + 1.2 s^2 + s
%
%
num=[1]; den=[0.2 1.2 1 0 ];
sys=tf(num,den);
w=logspace(-1,1,400);
nichols(sys,w);
ngrid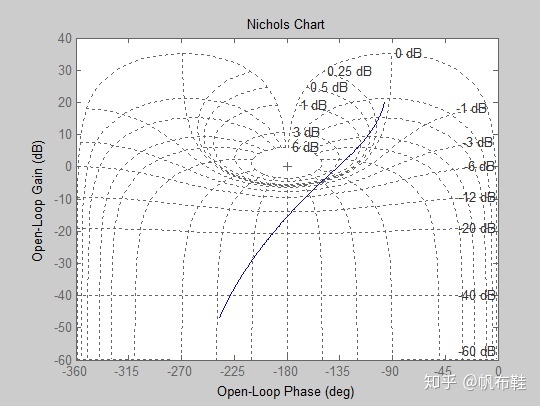
5. 使用伯德图来设计控制系统
考虑一个液压 控制系统的开环传递函数:
首先使用帕德近似,系统时延为T=1,近似的阶数取n=2,然后绘制增益裕度和相角裕度。
初始值K=31.5
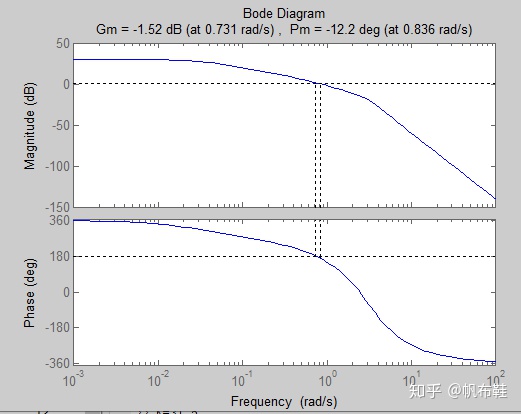
% The Bode plot of the liquid level control system with
% gain and phase margin. The gain K must be input at the
% command level before executing this m-file. Automatic
% labeling of the plot with gain and phase margin.
%
% Liquid Control System Analysis
%
[np,dp]=pade(1,2);
sysp=tf(np,dp);
num=K;
d1=[1 1]; d2=[30 1]; d3=[1/9 1/3 1];
den=conv(d1,conv(d2,d3));
sysg=tf(num,den);
sys=series(sysp,sysg);
%
margin(sys);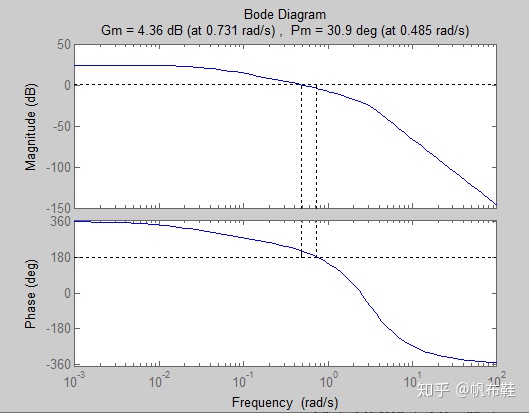
当K换成16时,验证系统的相角裕度满足了设计要求使相位裕度达到
6. 遥控侦探车的控制系统设计
考虑一个开环传递函数为
则首先考虑单位阶跃响应的稳态误差
再用频域方法考虑阶跃响应的超调量,若要求超调量小于50%,则近似地应该有
使用matlab计算闭环系统的伯德图
% Remotely controlled vehicle closed-loop system
% Bode plot for K=4.44, 10, and 20.
%
w=logspace(0,1,200); K=[20,10,4.44];
%
for i=1:3
numgc=K(i)*[1 2]; dengc=[1 1]; sysgc=tf(numgc,dengc);
numg=[1]; deng=[1 2 4]; sysg=tf(numg,deng);
syss=series(sysgc,sysg); sys=feedback(syss,[1]);
[mag,phase,w]=bode(sys,w);
mag_save(i,:)=mag(:,1,:);
end
%
loglog(w,mag_save(1,:),w,mag_save(2,:),w,mag_save(3,:))
xlabel('Frequency (rad/sec)'), ylabel('Magnitude'), grid on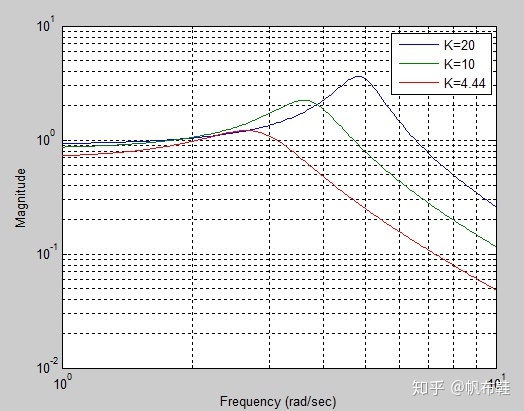
使用matlab计算K=4.44,10,20的情况下的阶跃响应。
% Remotely controlled vehicle closed-loop system
% step response for K=4.44, 10, and 20.
%
t=[0:0.01:10]; K=[20,10,4.44];
%
for i=1:3
numgc=K(i)*[1 2]; dengc=[1 1]; sysgc=tf(numgc,dengc);
numg=[1]; deng=[1 2 4]; sysg=tf(numg,deng);
syss=series(sysgc,sysg);
sys=feedback(syss,[1]);
y(:,i)=step(sys,t);
end
%
plot(t,y(:,1),t,y(:,2),t,y(:,3)),grid
xlabel('Time (sec)'), ylabel('y(t)')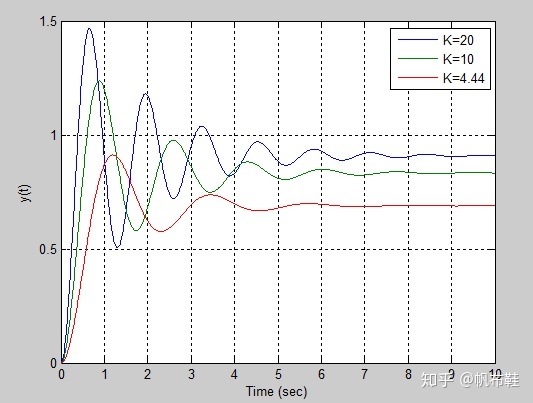
可以根据阶跃响应的超调量来确定增益K=20,K=10,K=4.44,也可以根据尼克尔斯图来完成系统的设计
% Remotely controlled vehicle system Nichols chart
% for K=4.44, 10, and 20.
%
numgc=[1 2]; dengc=[1 1]; sysgc=tf(numgc,dengc);
numg=[1]; deng=[1 2 4]; sysg=tf(numg,deng);
sys=series(sysgc,sysg);
%
w=logspace(-1,1,200);
%
K=[20, 10, 4.44];
hold off, clf
for i=1:3
nichols(K(i)*sys,w), ngrid
hold on
end
legend('K=20','K=10','K=4.44')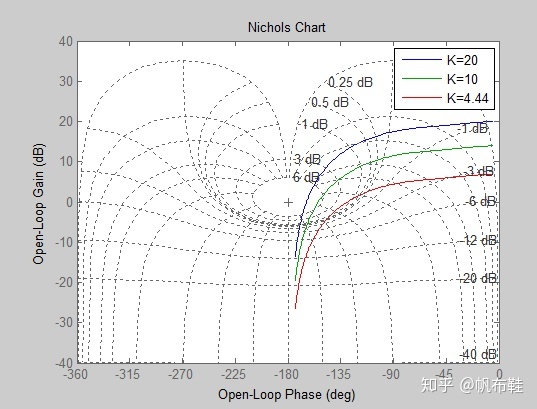
最后确定将增益的设计值选定为K=10,再绘制奈奎斯特图确定系统的相对稳定性,最终得到的增益裕度为G.M.=49.56 dB ,相角裕度为 P.M. =
% Remotely controlled vehicle system Nyquist chart
% for K= 10 with automatic labeling of gain and
% phase margin.
%
numgc=10*[1 2]; dengc=[1 1]; sysgc=tf(numgc,dengc);
numg=[1]; deng=[1 2 4]; sysg=tf(numg,deng);
%
sys=series(sysgc,sysg);
%
[Gm,Pm,Wcg,Wcp]=margin(sys);
%
nyquist(sys);
title(['Gm = ',num2str(Gm),' Pm = ',num2str(Pm)])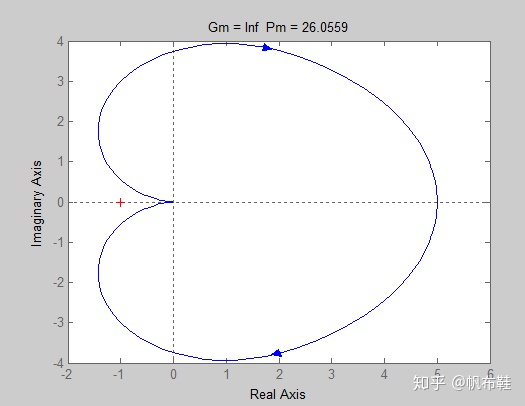
7. 循序渐进实例
考虑一个PD控制器
电机线圈
支撑臂
簧片与磁头
闭环控制系统为单位负反馈。
取K=400,则通过绘制伯德图,求增益裕度和相角裕度,以及阶跃响应。
K=400;
nc=K*[1 1]; dc=[0 1]; sysc=tf(nc,dc);
nm=[5]; dm=[0.001 1]; sysm=tf(nm,dm);
na=[0.05]; da=[0.05 1 0]; sysa=tf(na,da);
ng=[1]; dg=[1/18850^2 2*0.3/18850 1]; sysg=tf(ng,dg);
syso=series(sysc,series(sysm,series(sysa,sysg)))
figure(1)
margin(syso)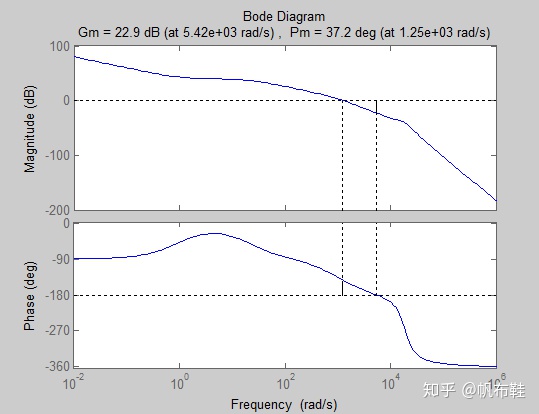
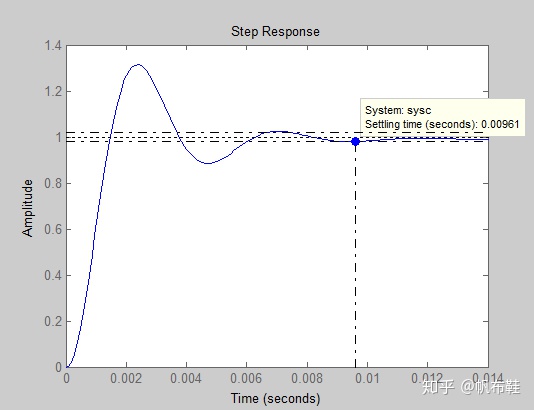
通过绘制伯德图可以得到系统的增益裕度为22.9 dB,相角裕度为
从阶跃响应曲线可以知道,调节时间为
最后
以上就是幸福啤酒最近收集整理的关于matlab曲线拟合幅频特性曲线_频域稳定性与matlab指令计算的全部内容,更多相关matlab曲线拟合幅频特性曲线_频域稳定性与matlab指令计算内容请搜索靠谱客的其他文章。








发表评论 取消回复