概述
摘要
常规测井方法：主要是指在油气勘探开发中,探井测井,评价井测井、开发井测井工程中都要测量的测井方法,
本文提出了一种利用** 随钻测井（LWD）**和测量(MWD)获得的钻井参数来实时预测伽马测井的方法，伽马测井被用作岩性识别器。我们使用不同的机器学习方法来测试它们捕捉流体机械比能(从钻井参数计算)与伽马射线测井之间关系的能力。
一：简介：
什么是随钻测井(LWD)：随钻测井一般是指在钻井的过程中测量地层岩石物理参数，并用数据遥测系统将测量结果实时送到地面进行处理。
为什么要随钻测井？：常规的随钻测井传感器(如伽马测井传感器)，通常放置在泥浆马达或旋转导向系统后面，以确定非常薄的储层取心点，但是这种方法成本高，通常情况下无法运行。所以我们要在钻头点获取钻井的参数。
岩性识别：确定油藏的大小、边界和性质(如渗透率)提供了一种手段。
伽马测井：为识别硅碎屑环境中的岩性变化提供了一种手段。
在这之前，其实就已经有人使用长短期记忆循环神经网络从其他测井参数生成目标测井参数。而我们的工作将测试几种传统机器学习算法(特别是那些具有序列建模功能的算法)的性能，测试它们使用钻井参数生成伽马射线测井的能力。
二：测井过程中的钻井参数
在这里我们将介绍在伽马射线测井中使用的钻井参数。
WOB——井下钻压(lb)，
Ab——钻头面积(in2)，
N——转速(rpm)，
ROP——钻速(ft/hr)，
T——扭矩(lb-ft)。
有了上面的参数，接下来提出机械比能(MSE)的概念：是移走一单位岩石所需的轴向能量和旋转能量之和，满足公式1
M
S
E
=
W
O
B
A
b
+
120
π
N
T
A
b
R
O
P
（公式
1
）
M S E=frac{W O B}{A_b}+frac{120 pi N T}{A_b R O P} （公式1）
MSE=AbWOB+AbROP120πNT（公式1）
在公式一的基础上，我们将钻头内的水力能量添加到MSE中，来削弱岩石对钻头的影响。我们就得到了流体力学比能(HMSE)
H
M
S
E
=
W
O
B
A
b
+
120
π
N
T
A
b
R
O
P
+
1154
η
Δ
P
b
Q
A
b
R
O
P
（公式
2
）
H M S E=frac{W O B}{A_b}+frac{120 pi N T}{A_b R O P} +frac{1154 eta Delta P_b Q}{A_b R O P} （公式2）
HMSE=AbWOB+AbROP120πNT+AbROP1154ηΔPbQ（公式2）其中
η
η
η为水力能量降低系数，
Δ
P
b
ΔPb
ΔPb为喷嘴处钻头压降(psi)，
Q
Q
Q为流量(gpm)，末尾新增的部分就是钻头的水力能量的表达式。
对于多晶金刚石致密钻头，η可以用式(3)计算。
η
P
D
C
b
i
t
=
1
−
(
J
S
A
T
F
A
)
−
0.122
(
公式
3
)
eta_{PDC_{bit}}=1-(frac{JSA}{TFA})^{-0.122} (公式3)
ηPDCbit=1−(TFAJSA)−0.122(公式3)这里JSA是指废料槽面积(
i
n
2
in^2
in2)， TFA是指流道面积(
i
n
2
in^2
in2)。
对于牙轮钻头(RCB)， η可用公式（4）计算：
η
R
C
B
=
1
−
(
0.15
B
i
t
a
r
e
a
T
F
A
)
−
0.122
(
公式
4
)
eta_{RCB}=1-(frac{0.15Bit area}{TFA})^{-0.122} (公式4)
ηRCB=1−(TFA0.15Bitarea)−0.122(公式4)
喷嘴处钻头压降
Δ
P
b
ΔPb
ΔPb，可用计算公式5计算：
Δ
P
b
=
M
W
Q
2
10858
T
F
A
2
（公式
5
）
Delta P_b=frac{M W Q^2}{10858 T F A^2}（公式5）
ΔPb=10858TFA2MWQ2（公式5）其中MW为泥浆重量(PPG)， Q为流速(gpm)。
到这里我们又发现了除了岩性变化，其他一些因素，如岩石压实和钻头磨损，也会影响HMSE的值。比如说岩石压实度通常随着深度的增加而增加，这导致了HMSE的增加。所以我们还需要对公式2进行改进，于是我们将孔隙压实模型应用于公式2中，得到一个新的表达式
H
M
S
E
d
n
=
(
W
O
B
A
b
+
120
π
N
T
A
b
R
O
P
+
1154
η
Δ
P
b
Q
A
b
R
O
P
)
∅
0
e
−
K
Z
（公式
6
）
H M S E_{d n}=left(frac{W O B}{A_b}+frac{120 pi N T}{A_b R O P}+frac{1154 eta Delta P_b Q}{A_b R O P}right) varnothing_0 e^{-K Z}（公式6）
HMSEdn=(AbWOB+AbROP120πNT+AbROP1154ηΔPbQ)∅0e−KZ（公式6）
H
M
S
E
d
n
HMSE_{dn}
HMSEdn表示深度效应归一化HMSE。
∅
0
varnothing_0
∅0为地表或泥线孔隙度，
Z
Z
Z为垂向真深(ft)，
K
K
K为压实系数(1/ft)。
∅
0
varnothing_0
∅0和
K
K
K的值可由探边井计算得到。到这里我们需要使用的钻井参数就介绍完了。
在这之前已经有研究表明伽马射线测井与
H
M
S
E
d
n
HMSE_{dn}
HMSEdn之间存在明显的相关性,而我们工作目标是利用机器学习捕获HMSEdn和伽马射线测井之间的关系。
三：本文使用到的机器学习算法
首先解释一下为什么要用多种机器学习方法：因为对于不同的任务，机器学习算法可能具有不同的相对性能。
3.1：人工神经网络(ANN)：
一个简单的神经网络由一个输入层、一个或几个简单的隐藏层和一个输出层组成。如下图1所示。
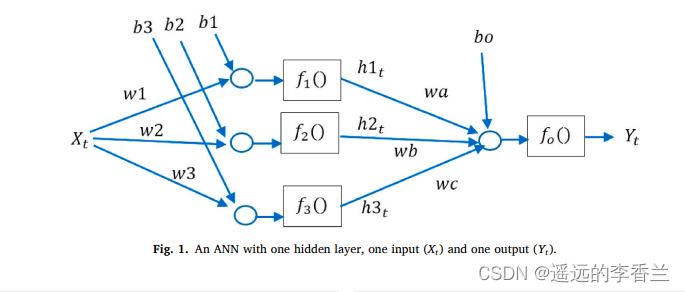
在图1中，输入层由输入组成。隐含层包括以下权重
w
1
w1
w1、
w
2
w2
w2和
w
3
w3
w3，偏差
b
1
b1
b1、
b
2
b2
b2和
b
3
b3
b3，圆形O表示的节点是一个求和点。节点激活函数（非线性s）
f
1
(
)
f_1()
f1()、
f
2
(
)
f_2()
f2()和
f
3
(
)
f_3()
f3()以及计算值
h
1
t
h1_t
h1t、
h
2
t
h2_t
h2t和
h
3
t
h3_t
h3t。输出层包括权重
w
a
wa
wa,
w
b
wb
wb和
w
c
wc
wc，节点激活函数fo()和计算值
Y
t
Y_t
Yt。如何计算以
X
t
X_t
Xt作为自变量的函数
Y
t
Y_t
Yt的值呢？接着往下看。
计算函数
f
1
(
)
f_1()
f1()得到
h
1
t
h1_t
h1t:
h
1
t
=
f
1
(
w
1
×
X
t
+
b
1
)
（公式
7
）
h1_t=f_1(w 1 × X_t + b1) （公式7）
h1t=f1(w1×Xt+b1)（公式7）
计算函数
f
2
(
)
f_2()
f2()得到
h
2
t
h2_t
h2t:
h
2
t
=
f
2
(
w
2
×
X
t
+
b
2
)
（公式
8
）
h2_t=f_2(w 2 × X_t + b2)（公式8）
h2t=f2(w2×Xt+b2)（公式8）
计算函数
f
3
(
)
f_3()
f3()得到
h
3
t
h3_t
h3t:
h
3
t
=
f
1
(
w
3
×
X
t
+
b
3
)
（公式
9
）
h3_t=f_1(w 3 × X_t + b3)（公式9）
h3t=f1(w3×Xt+b3)（公式9）
计算
Y
t
Y_t
Yt:
Y
t
=
f
0
(
w
a
×
h
1
t
+
w
b
×
h
2
t
+
w
c
×
h
3
t
+
b
o
)
（公式
10
）
Y_t=f_0(w a × h1_t + wb × h2_t + wc × h3_t +bo) （公式10）
Yt=f0(wa×h1t+wb×h2t+wc×h3t+bo)（公式10）
3.2：循环神经网络(RNN)
简单的人工神经网络和简单的循环神经网络RNN之间的主要区别是在循环神经网络的隐藏层中有一个反馈连接。如图2所示。
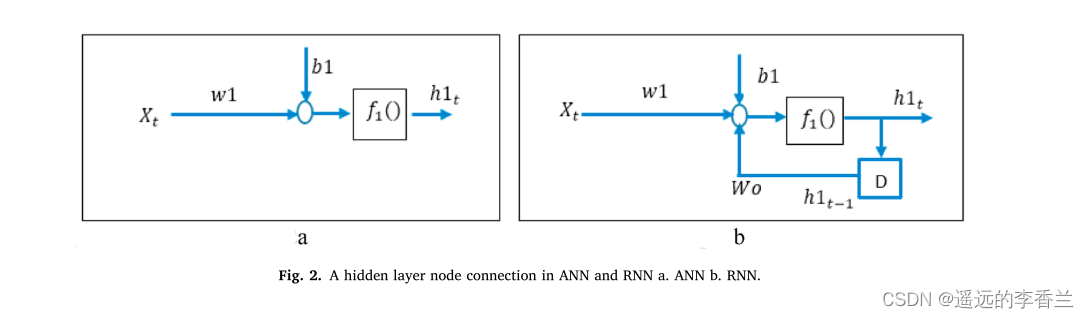
左边图a表示了图1隐层中的一个节点，图b表示增加一个单位延迟D，将f1()的输出传递回节点，以实现简单的RNN。这时计算公式就会发生一些变化，比如在循环神经网络中计算
h
1
t
h1_t
h1t:
h
1
t
=
f
1
(
w
1
×
X
t
+
W
o
×
h
1
t
−
1
+
b
1
)
（公式
11
）
h1_t=f_1(w 1 × X_t +W o ×h1_{t-1} + b1) （公式11）
h1t=f1(w1×Xt+Wo×h1t−1+b1)（公式11）由式子可以看出
h
1
t
h1_t
h1t是
h
1
t
−
1
h1_{t−1}
h1t−1和
X
t
X_t
Xt的函数。同样，
h
1
t
−
1
h1_{t−1}
h1t−1是
h
1
t
−
2
h1_{t−2}
h1t−2和
X
t
−
1
X_{t−1}
Xt−1的函数。这表明
h
1
t
h1_t
h1t可以捕捉输入x的现在和所有过去的值。因此，对于一个简单的RNN，当前的输出是输入的当前值和所有过去值的函数。
3.3：具有外生输入的非线性自回归网络(NARX)
NARX与简单的RNN非常相似。主要区别是:(1)NARX中存在输出到输入的反馈连接，也就是
Y
t
Y_t
Yt到隐藏层，而RNN的反馈链接只存在于隐藏层之中，例如图2所示的
h
1
t
−
1
h1_{t-1}
h1t−1;(2)增加延迟线以吸收过去的输入值。 NARX如图3所示。
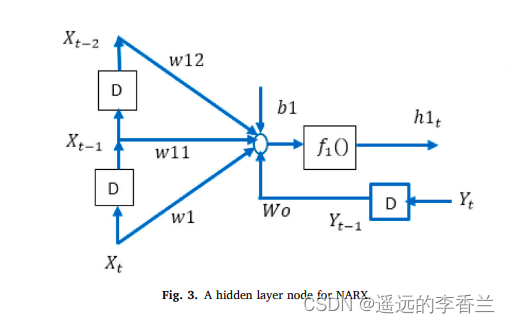
然后我们将公式11修改成公式12，来计算NARX 中的
h
1
t
h1_t
h1t
h
1
t
=
f
1
(
w
1
×
X
t
+
W
11
×
X
t
−
1
+
w
12
×
X
t
−
2
+
W
o
×
Y
t
−
1
+
b
1
)
（公式
12
）
h1_t=f_1(w 1 × X_t +W11 ×X_{t-1} + w 12 × X_{t-2} +Wo × Y_{t-1} + b1 ) （公式12）
h1t=f1(w1×Xt+W11×Xt−1+w12×Xt−2+Wo×Yt−1+b1)（公式12）
3.4长短时记忆循环神经网络(LSTM-RNN)
LSTM如图4所示：
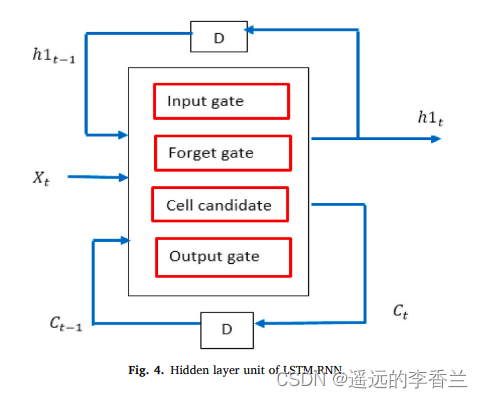图4中有输入门(Input gate)
G
i
t
Gi_t
Git、忘记门(Forget gate)
G
f
t
Gf_t
Gft、单元格候选(Cell candidate)
G
c
t
Gc_t
Gct和输出门(Output gate)
G
o
t
Go_t
Got四个组件在训练过程中帮助学习，四个组件中的每一个都是当前输入值
X
t
X_t
Xt和之前
h
1
h1
h1(疑问：这里为什么不是
h
1
t
−
1
h1_{t-1}
h1t−1)值即
h
1
t
−
1
h1_{t−1}
h1t−1的函数.它们的计算公式如下所示:
G
i
t
=
F
s
(
X
t
×
w
i
)
+
(
h
1
t
−
1
×
v
i
)
+
b
i
（公式
13
）
Gi_t = F_s{(X_t × wi) + (h1_{t−1} × vi) + bi}（公式13）
Git=Fs(Xt×wi)+(h1t−1×vi)+bi（公式13）
G
f
t
=
F
s
(
X
t
×
w
f
)
+
(
h
1
t
−
1
×
v
f
)
+
b
f
（公式
14
）
Gf_t = F_s{(X_t × wf ) + (h1_{t−1} × vf ) + bf } （公式14）
Gft=Fs(Xt×wf)+(h1t−1×vf)+bf（公式14）
G
c
t
=
F
h
(
X
t
×
w
c
)
+
(
h
1
t
−
1
×
v
c
)
+
b
c
（公式
15
）
Gc_t = F_h{(X_t × wc) + (h1_{t−1} × vc) + bc}（公式15）
Gct=Fh(Xt×wc)+(h1t−1×vc)+bc（公式15）
G
o
t
=
F
s
(
X
t
×
w
o
)
+
(
h
1
t
−
1
×
v
o
)
+
b
o
（公式
16
）
Go_t = F_s{(X_t × wo) + (h1_{t−1} × vo) + bo}（公式16）
Got=Fs(Xt×wo)+(h1t−1×vo)+bo（公式16）其中
W
i
、
w
f
、
w
c
、
w
o
、
v
i
、
v
f
、
v
c
、
v
o
Wi、wf、wc、wo、vi、vf、vc、vo
Wi、wf、wc、wo、vi、vf、vc、vo为与各自分量相关的权重，
b
i
、
b
f
、
B
C
、
b
o
bi、bf、BC、bo
bi、bf、BC、bo为各自分量对应的偏置值。需要注意的是，Fs和Fh是sigmoid (logistic)和双曲切线激活函数。计算公式为17和18。
F
s
{
z
}
=
1
1
+
e
−
z
（公式
17
）
F_s{z}=frac{1}{1+e^{-z}}（公式17）
Fs{z}=1+e−z1（公式17）
F
h
{
z
}
=
t
a
n
h
(
z
)
（公式
18
）
F_h{z}=tanh(z) （公式18）
Fh{z}=tanh(z)（公式18）此外我们注意到上图中还有个
C
t
C_t
Ct，它是t处的记忆单元值，其计算公式为：
C
t
=
(
G
f
t
×
C
t
−
1
)
+
(
G
c
t
×
G
i
t
)
（公式
19
）
C_t = (Gf_t × C_{t−1}) + (Gc_t × Gi_t) （公式19）
Ct=(Gft×Ct−1)+(Gct×Git)（公式19）对于LSTM单元，
h
1
t
h1_t
h1t是输出门和存储单元值的函数:
h
1
t
=
G
o
t
×
F
h
C
t
（公式
20
）
h1_t = Go_t × F_h{C_t}（公式20）
h1t=Got×FhCt（公式20）
3.5门控循环单元(GRU)网络
GRU可以看作是LSTM的简化衍生物，但有一些变化。尽管GRU相对简化，但其性能仍可与LSTM-RNN相媲美.GRU将LSTM的输入门、遗忘门、输出门和单元候选替换为更新门
G
u
t
Gu_t
Gut、重置门
G
r
t
Gr_t
Grt和隐藏状态候选
G
h
t
Gh_t
Ght。计算公式如下：
G
u
t
=
F
s
(
X
t
×
w
u
)
+
(
h
1
t
−
1
×
v
u
)
+
b
u
（公式
21
）
Gu_t = F_s{(X_t × wu) + (h1_{t−1} × vu) + bu}（公式21）
Gut=Fs(Xt×wu)+(h1t−1×vu)+bu（公式21）
G
r
t
=
F
s
(
X
t
×
w
r
)
+
(
h
1
t
−
1
×
v
r
)
+
b
r
（公式
22
）
Gr_t = F_s{(X_t × wr) + (h1_{t−1} × vr) + br}（公式22）
Grt=Fs(Xt×wr)+(h1t−1×vr)+br（公式22）
G
h
t
=
F
h
(
X
t
×
w
h
)
+
(
(
G
r
t
×
h
1
t
−
1
)
×
v
h
)
+
b
h
（公式
23
）
Gh_t = F_h{(X_t × wh) + ((Gr_t × h1_{t−1}) × vh) + bh}（公式23）
Ght=Fh(Xt×wh)+((Grt×h1t−1)×vh)+bh（公式23）
h
1
t
=
h
1
t
−
1
×
(
1
−
G
u
t
)
+
G
h
t
×
G
u
t
（公式
24
）
h1_t = h1_{t−1} × (1 − Gu_t) + Gh_t × Gu_t（公式24）
h1t=h1t−1×(1−Gut)+Ght×Gut（公式24）
四：利用钻井参数和机器学习生成伽马测井的方法
利用钻井参数和机器学习生成伽马测井的方法流程图如下图所示：
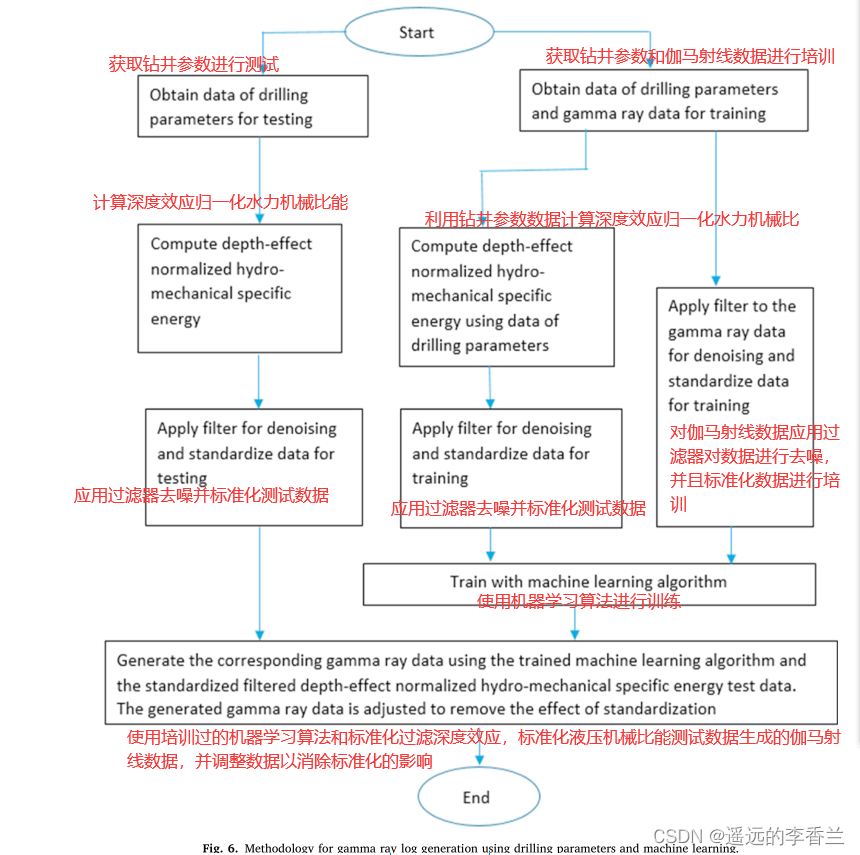
4.1获取用于训练和测试的钻井参数和伽马射线数据：
计算
H
M
S
E
d
n
HMSE_{dn}
HMSEdn所需的钻井参数数据与伽马测井一起获得,并且我们预计用于训练的
H
M
S
E
d
n
HMSE_{dn}
HMSEdn和伽马射线测井将足以捕获测试数据中的关系。
4.2过滤和标准化方法
采用长度为5的移动平均(mean)作为伽马射线测井的滤波器，以抑制噪声变化。对HMSEdn数据进行了相同的过滤操作。经过过滤后，得到的伽马射线测井和HMSEdn数据被标准化用于机器学习。使用训练数据的均值和标准差对数据进行标准化。标准化公式如下所示：
G
t
r
a
i
n
n
=
(
G
t
r
a
i
n
−
μ
G
)
/
σ
G
（公式
25
）
Gtrain_n = (Gtrain − μ_G)/σ_G（公式25）
Gtrainn=(Gtrain−μG)/σG（公式25）
H
t
r
a
i
n
n
=
(
H
t
r
a
i
n
−
μ
H
)
/
σ
H
（公式
26
）
Htrain_n = (Htrain − μ_H)/σ_H（公式26）
Htrainn=(Htrain−μH)/σH（公式26）
H
t
e
s
t
n
=
(
H
t
e
s
t
−
μ
H
)
/
σ
H
（公式
27
）
Htest_n = (Htest − μ_H)/σ_H（公式27）
Htestn=(Htest−μH)/σH（公式27）其中Gtrain为过滤后训练的伽马射线测井数据、Htrain为过滤后训练的
H
M
S
E
d
n
HMSE_{dn}
HMSEdn数据。滤波后测试的
H
M
S
E
d
n
HMSE_{dn}
HMSEdn数据为Htest。
μ
G
μ_G
μG和
σ
G
σ_G
σG分别代表Gtrain的均值和标准差，
μ
H
μ_H
μH和
σ
H
σ_H
σH分别代表Htrain的均值和标准差。在训练神经网络后，将
H
t
e
s
t
n
Htest_n
Htestn输入到神经网络中，这将产生一个输出(Goutput)。这个输出(Goutput)是重新调整，通过消除标准化的影响使用方程。最后我们生成的伽马射线测井为：
G
g
e
n
e
r
a
t
e
=
(
σ
G
×
G
o
u
t
p
u
t
)
+
μ
G
（公式
28
）
Ggenerate = (σ_G × Goutput) + μ_G（公式28）
Ggenerate=(σG×Goutput)+μG（公式28）
4.3机器学习算法的配置和训练
文中所使用的各种机器学习算法的配置和训练选项总结如下表1所示
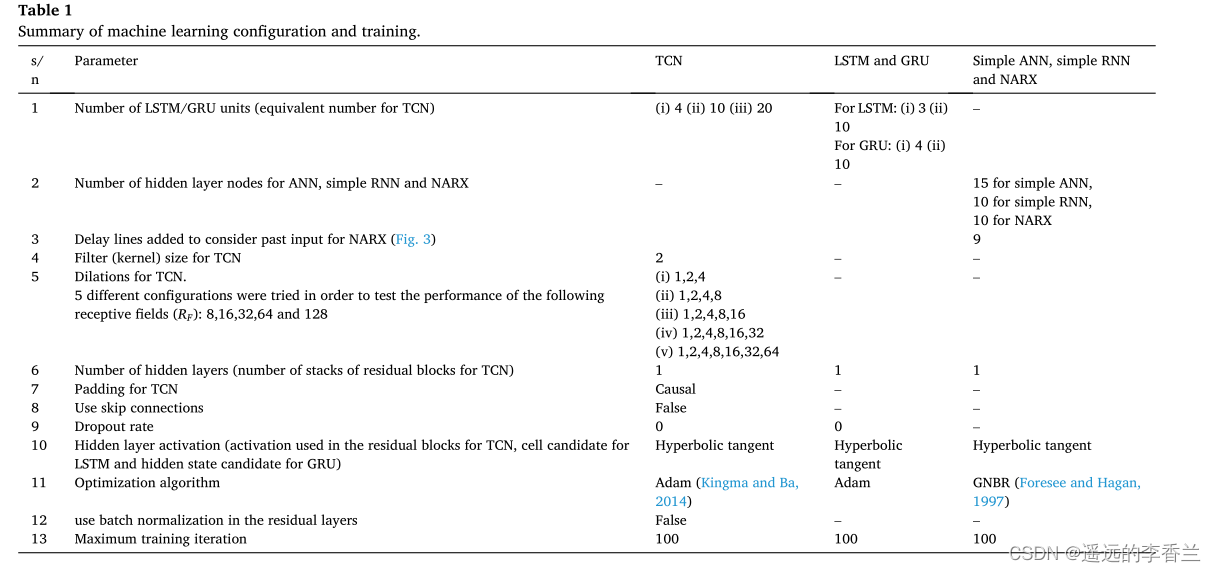
五：结果
以尼日尔三角洲盆地中部沼泽地区的一口气井为例进行了研究，以此来证明我们的方法。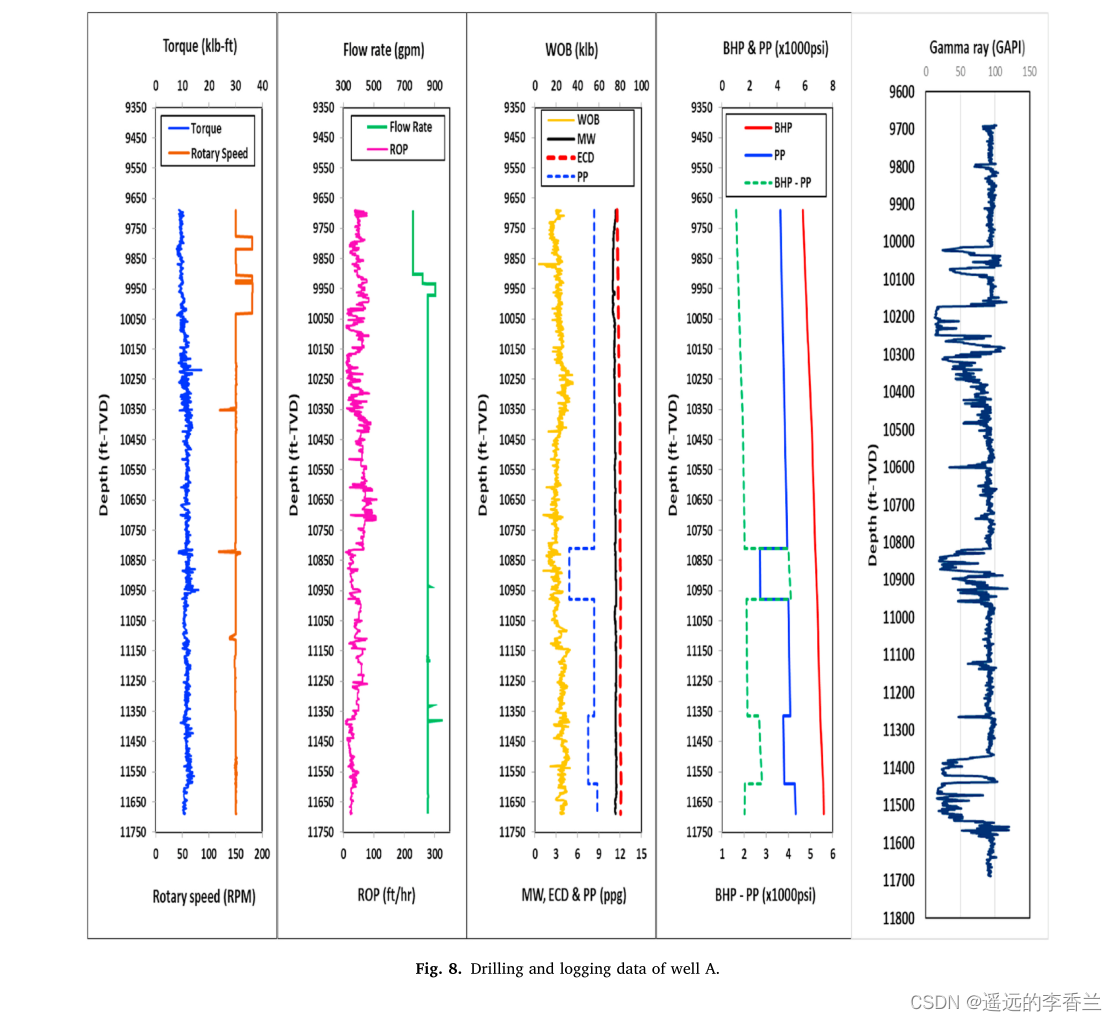
上图显示了钻井参数数据(扭矩、转速、流量、钻速、钻压、泥浆重量和等效循环密度，即ECD)、随钻参数(伽马射线)、井孔压力(PP)和井底压力(BHP),为计算(公式6)所示的深度效应归一化，采用偏置井法求得相应的
∅
0
varnothing_0
∅0和
K
K
K值。由此得出
∅
0
varnothing_0
∅0为0.54,
K
K
K为0.0001。
5.1、去噪
我们可以采用第四节中所说的滤波器进行滤波——采用长度为5的移动平均(mean)作为伽马射线测井的滤波器，以抑制噪声变化。
过滤前的伽马射线测井如图所示：
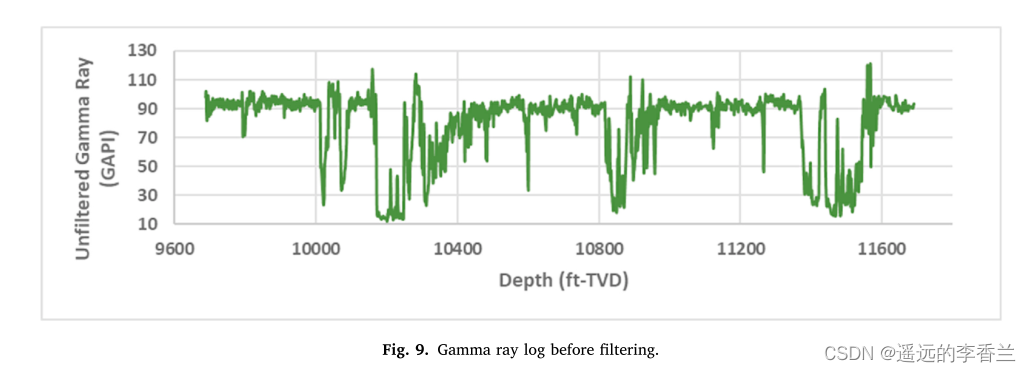
过滤后的伽马射线测井如图所示：
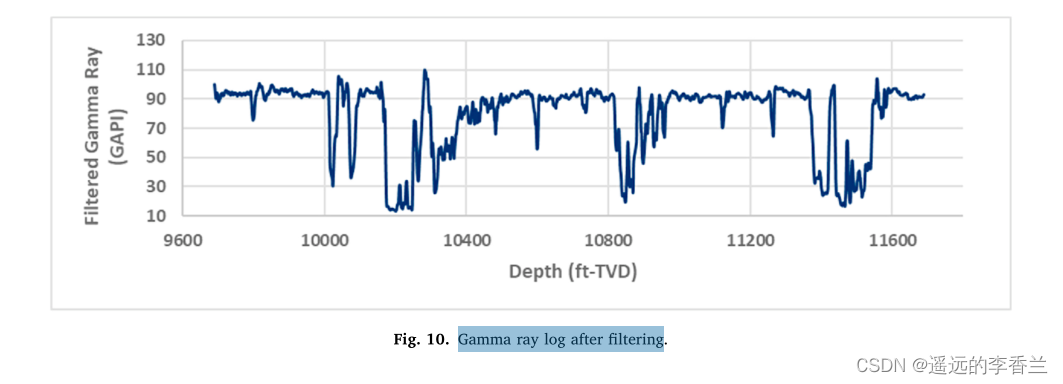
用（公式6)得到的深度归一化流体力学比能
H
M
S
E
d
n
HMSE_{dn}
HMSEdn的结果也用上面描述的相同滤波器进行滤波。并且将深度归一化流体力学比能
H
M
S
E
d
n
HMSE_{dn}
HMSEdn与伽马射线测井进行比较。比较结果如下图所示：
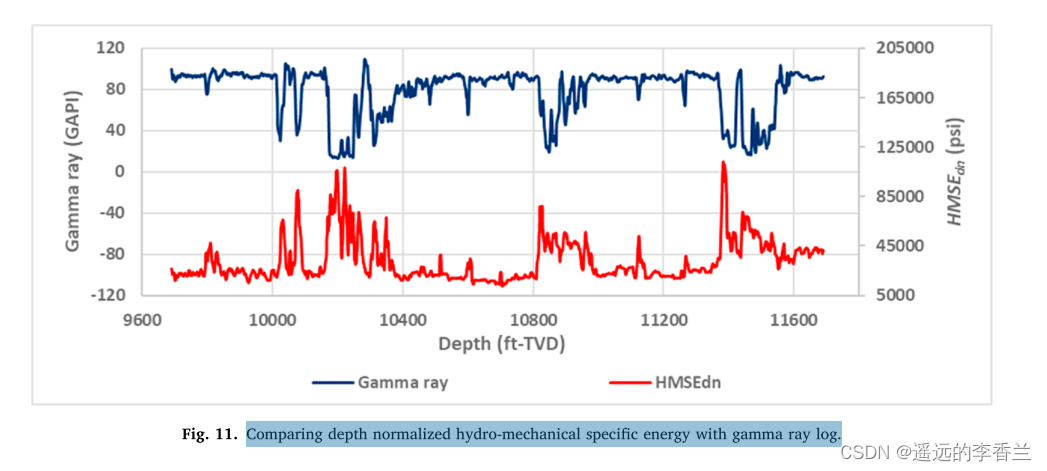
从上面的图我们可以很清晰的看见深度归一化流体力学比能
H
M
S
E
d
n
HMSE_{dn}
HMSEdn与伽马射线测井具有很好的匹配关系。我们用HMSEdn与伽马射线测井图观察相关性：
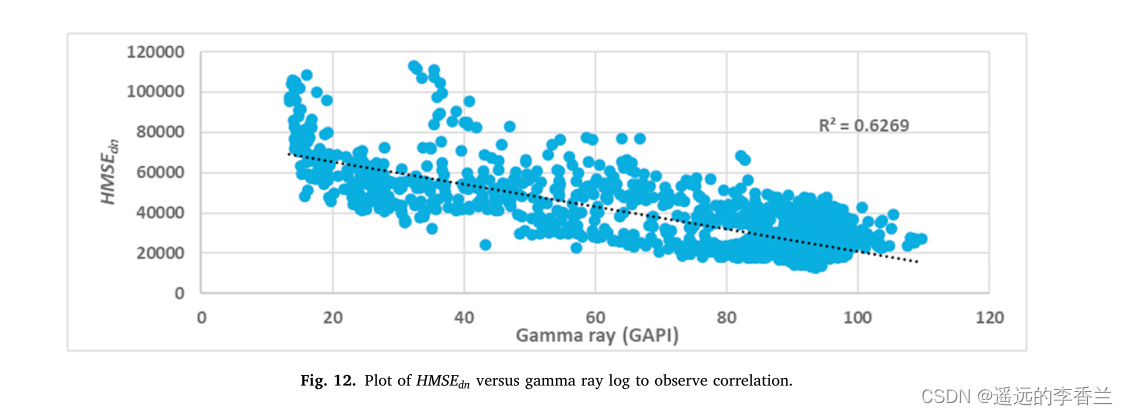
5.2远端伽马射线测井生成
远端伽马射线测井生成相当于在已有钻井参数值的情况下，实时预测钻井深度的测井参数值。在这个过程中我们将
H
M
S
E
d
n
HMSE_{dn}
HMSEdn和伽马射线测井分为训练和测试部分（初始75%的数据(1428个数据点)用于训练，其余25%的数据(477个数据点)用于测试），如下图所示。
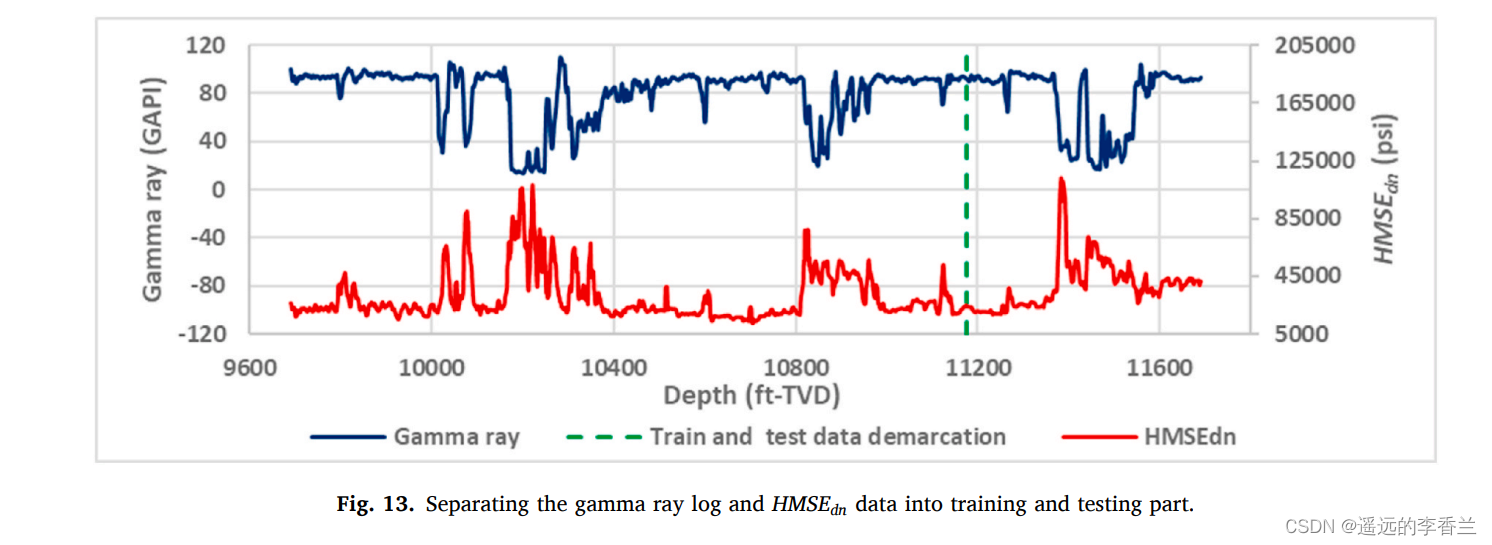
训练和测试的结果如下表2所示：
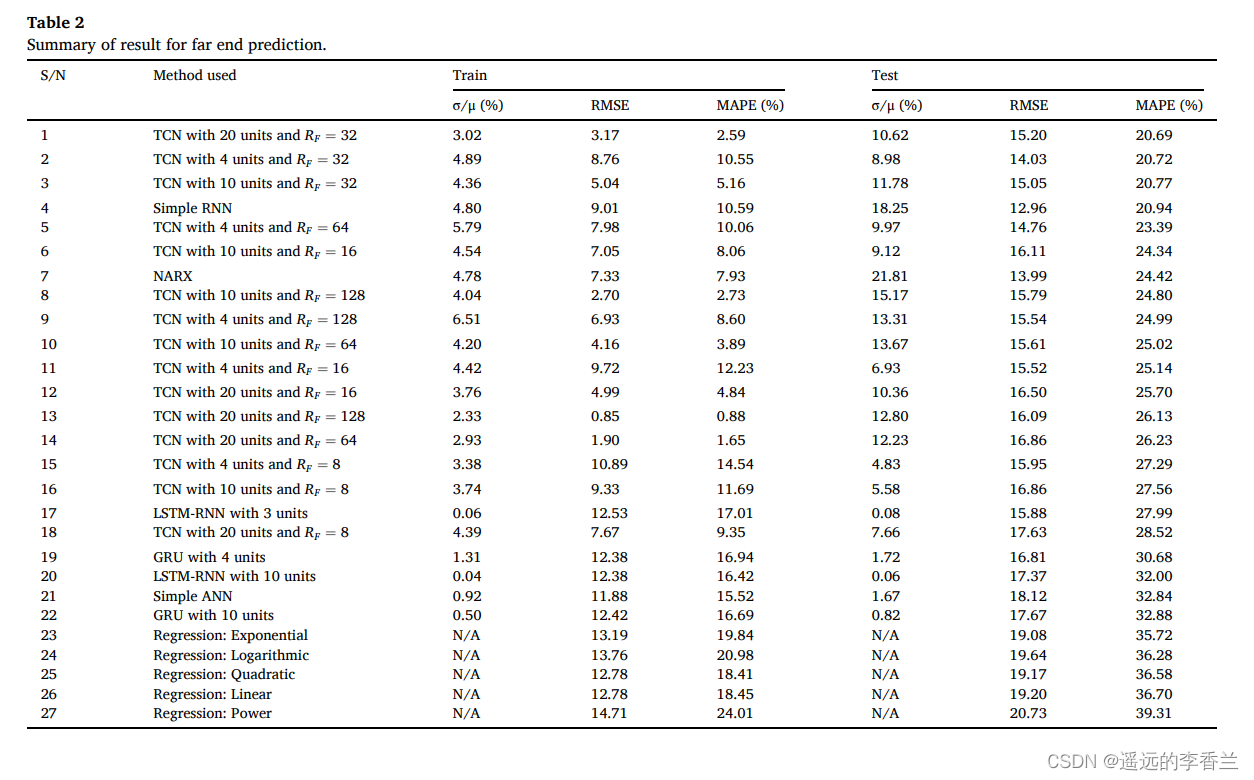
需要注意的是，表2的结果并不是为了比较机器学习算法的优势，而是显示了数据的规模和复杂性(如第3.0节所述)以及机器学习算法的配置会显著影响性能。尽管TCN和简单RNN的性能优于LSTM-RNN(表2)，但可以观察到，当LSTM-RNN对每个输出数据点强制使用给定的输入数据窗口(当前加上之前的31个输入数据点)时(如表3所示)，
表3如下所示：
LSTM-RNN的性能显著提高。
总结
本文提出了一种利用钻井参数生成伽马测井曲线的方法。这涉及到从钻井参数计算深度效应归一化流体力学比能(
H
M
S
E
d
n
HMSE_{dn}
HMSEdn)。使用机器学习来捕获
H
M
S
E
d
n
HMSE_{dn}
HMSEdn和伽马射线测井之间的关系，以便执行两类任务:(1)生成实时岩性分析所需的井远端伽马射线测井;（2）伽马射线测井中缺失剖面的生成
结果表明TCN和简单RNN的效果最好。TCN的接受场在其性能中发挥了重要作用，因此，如果手动使LSTM-RNN工作在每个输出数据点的输入数据点的最优窗口，那么LSTM-RNN的性能可以与TCN/简单RNN相当。数据的大小和性质(数量、速度、种类和准确性)可能是影响机器学习方法性能的一个重要因素。因此，建议在机器学习开发阶段集中精力获取数据的最佳接受域。
最后
以上就是温暖茉莉为你收集整理的阅读笔记五：Gamma ray log generation from drilling parameters using deep learning的全部内容，希望文章能够帮你解决阅读笔记五：Gamma ray log generation from drilling parameters using deep learning所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复