密码学

Hash 算法与数字摘要

Hash（哈希或散列）算法，又常被称为指纹（fingerprint）或摘要（digest）算法，是非常基础也非常重要的一类算法。可以将任意长度的二进制明文串映射为较短的（通常是固定长度的）二进制串（Hash 值），并且不同的明文很难映射为相同的 Hash 值。

例如计算 “hello blockchain world, this is yeasy@github” 的 SHA-256 Hash 值。

$ echo "hello blockchain world, this is yeasy@github"|shasum -a 256
db8305d71a9f2f90a3e118a9b49a4c381d2b80cf7bcef81930f30ab1832a3c90

SHA-2，名称来自于安全散列算法2（英语：Secure Hash Algorithm 2）的缩写。对于任意长度的消息，SHA256都会产生一个256bit长的哈希值，称作消息摘要。

一个优秀的 Hash 算法，将能满足：

• 正向快速：给定原文和 Hash 算法，在有限时间和有限资源内能计算得到 Hash 值；
• 逆向困难：给定（若干）Hash 值，在有限时间内无法（基本不可能）逆推出原文；
• 输入敏感：原始输入信息发生任何改变，新产生的 Hash 值都应该发生很大变化；
• 碰撞避免：很难找到两段内容不同的明文，使得它们的 Hash 值一致（即发生碰撞）

常见hash算法

目前常见的 Hash 算法包括国际上的 Message Digest（MD）系列和 Secure HashAlgorithm（SHA）系列算法，以及国内的 SM3 算法。

MD 算法主要包括 MD4 和 MD5 两个算法。MD4（RFC 1320）是 MIT 的 Ronald L. Rivest在 1990 年设计的，其输出为 128 位。MD4 已证明不够安全。MD5（RFC 1321）是 Rivest于 1991 年对 MD4 的改进版本。它对输入仍以 512 位进行分组，其输出是 128 位。MD5 比MD4 更加安全，但过程更加复杂，计算速度要慢一点。MD5 已于 2004 年被成功碰撞，其安全性已不足应用于商业场景。。

SHA 算法由美国国家标准与技术院（National Institute of Standards and Technology，NIST）征集制定。首个实现 SHA-0 算法于 1993 年问世，1998 年即遭破解。随后的修订版本 SHA-1 算法在 1995 年面世，它的输出为长度 160 位的 Hash 值，安全性更好。SHA-1 设计采用了 MD4 算法类似原理。SHA-1 已于 2005 年被成功碰撞，意味着无法满足商用需求。为了提高安全性，NIST 后来制定出更安全的 SHA-224、SHA-256、SHA-384，和 SHA-512算法（统称为 SHA-2 算法）。新一代的 SHA-3 相关算法也正在研究中。

此外，中国密码管理局于 2010 年 12 月 17 日发布了GM/T 0004-2012 《SM3 密码杂凑算法》，建立了国内商用密码体系中的公开 Hash 算法标准，已经被广泛应用在数字签名和认证等场景中。
注：MD5 和 SHA-1 算法的破解工作都是由清华大学教授、中国科学院院士王小云主导完成。

数字摘要

数字摘要是 Hash 算法重要用途之一。顾名思义，数字摘要是对原始的数字内容进行 Hash 运算，获取唯一的摘要值。

利用 Hash 函数抗碰撞性特点，数字摘要可以检测内容是否被篡改过。

细心的读者可能会注意到，有些网站在提供文件下载时，会同时提供相应的数字摘要值。用
户下载原始文件后可以在本地自行计算摘要值，并与所提供摘要值进行比对，以确保文件内
容没有被篡改过。

加解密算法

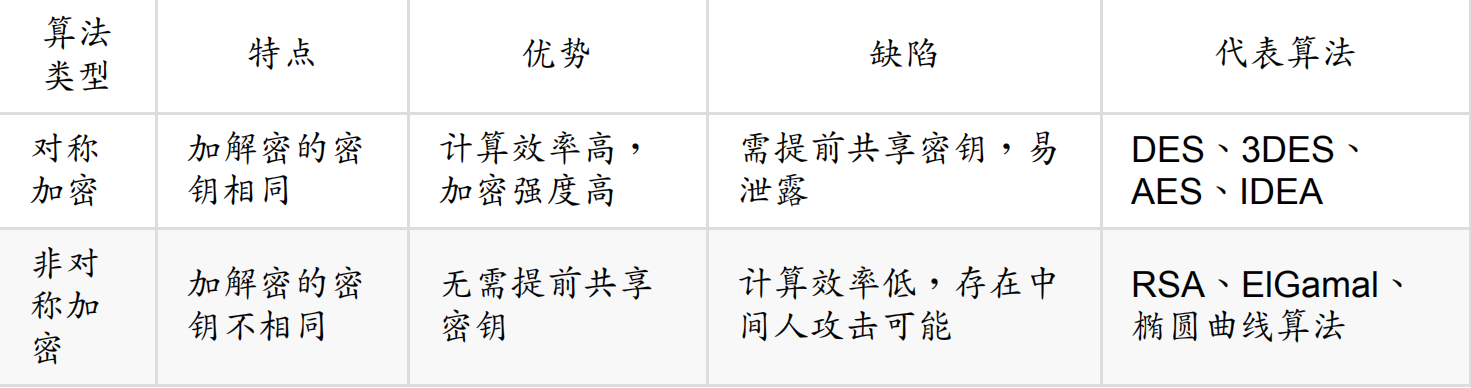
加解密算法是现代密码学核心技术，从设计理念和应用场景上可以分为两大基本类型，如下表所示：

加解密系统基本组成

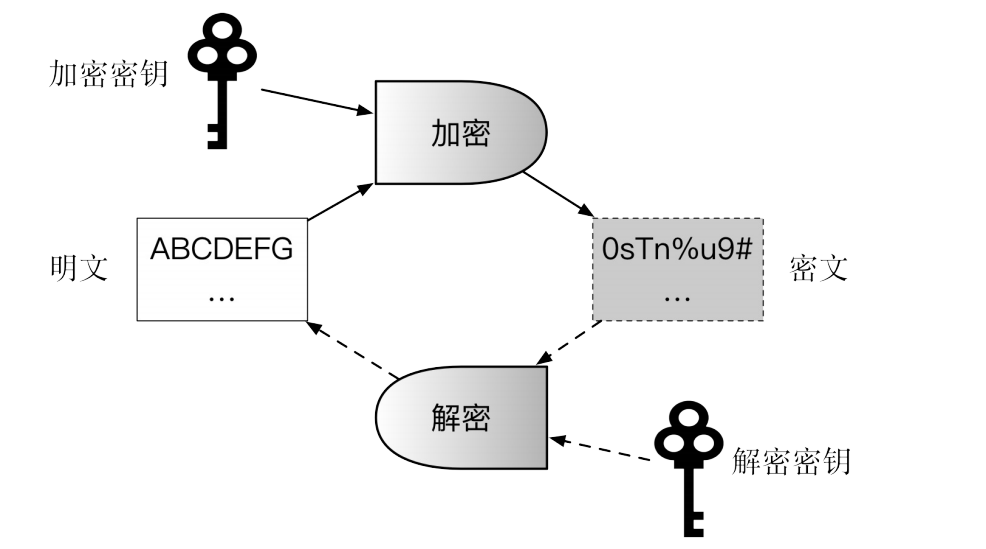
现代加解密系统的典型组件包括算法和密钥（包括加密密钥、解密密钥）。

其中，加解密算法自身是固定不变的，并且一般是公开可见的；密钥则是最关键的信息，需要安全地保存起来，甚至通过特殊硬件进行保护。一般来说，密钥需要在加密前按照特定算法随机生成，长度越长，则加密强度越大。

加解密的典型过程如下图所示。加密过程中，通过加密算法和加密密钥，对明文进行加密，获得密文；解密过程中，通过解密算法和解密密钥，对密文进行解密，获得明文。

对称加密算法

对称加密算法，顾名思义，加密和解密过程的密钥是相同的。

该类算法优点是加解密效率（速度快，空间占用小）和加密强度都很高。
缺点是参与方需要提前持有密钥，一旦有人泄露则系统安全性被破坏；另外如何在不安全通道中提前分发密钥也是个问题，需要借助额外的 Diffie–Hellman 协商协议或非对称加密算法来实现。

对称密码从实现原理上可以分为两种：分组密码和序列密码。前者将明文切分为定长数据块作为基本加密单位，应用最为广泛。后者则每次只对一个字节或字符进行加密处理，且密码不断变化，只用在一些特定领域（如数字媒介的加密）。

总结下，对称加密算法适用于大量数据的加解密过程；不能用于签名场景；并且需要提前安全地分发密钥。

非对称加密算法

非对称加密是现代密码学的伟大发明，它有效解决了对称加密需要安全分发密钥的问题。

顾名思义，非对称加密中，加密密钥和解密密钥是不同的，分别被称为公钥（Public Key）和私钥（Private Key）。私钥一般通过随机数算法生成，公钥可以根据私钥生成。

其中，公钥一般是公开的，他人可获取的；私钥则是个人持有并且要严密保护，不能被他人获取。

非对称加密算法优点是公私钥分开，无需安全通道来分发密钥。缺点是处理速度（特别是生成密钥和解密过程）往往比较慢，一般比对称加解密算法慢 2~3 个数量级；同时加密强度也往往不如对称加密。

非对称加密算法的安全性往往基于数学问题，包括大数质因子分解、离散对数、椭圆曲线等经典数学难题。代表算法包括：RSA、ElGamal、椭圆曲线（Elliptic Curve Crytosystems，ECC）、SM2 等系列算法。

消息认证码与数字签名

消息认证码和数字签名技术通过对消息的摘要进行加密，可以防止消息被篡改和认证身份。

消息认证码

消息认证码（Hash-based Message Authentication Code，HMAC），利用对称加密，对消息完整性（Integrity）进行保护。

基本过程为对某个消息，利用提前共享的对称密钥和 Hash 算法进行处理，得到 HMAC 值。该 HMAC 值持有方可以向对方证明自己拥有某个对称密钥，并且确保所传输消息内容未被篡改。

典型的 HMAC 生成算法包括 K，H，M 三个参数。K 为提前共享的对称密钥，H 为提前商定的 Hash 算法（如 SHA-256），M 为要传输的消息内容。三个参数缺失了任何一个，都无法得到正确的 HMAC 值。

消息认证码可以用于简单证明身份的场景。如 Alice、Bob 提前共享了 K 和 H。Alice 需要知晓对方是否为 Bob，可发送一段消息 M 给 Bob。Bob 收到 M 后计算其 HMAC 值并返回给Alice，Alice 检验收到 HMAC 值的正确性可以验证对方是否真是 Bob。注：例子中并没有考虑中间人攻击的情况，并假定信道是安全的。消息认证码的主要问题是需要提前共享密钥，并且当密钥可能被多方同时拥有（甚至泄露）
的场景下，无法追踪消息的真实来源。如果采用非对称加密算法，则能有效的解决这个问题，即数字签名。

数字签名

一个典型的场景是，Alice 通过信道发给 Bob 一个文件（一份信息），Bob 如何获知所收到的文件即为 Alice 发出的原始版本？Alice 可以先对文件内容进行摘要，然后用自己的私钥对摘要进行加密（签名），之后同时将文件和签名都发给 Bob。Bob 收到文件和签名后，用 Alice
的公钥来解密签名，得到数字摘要，与对文件进行摘要后的结果进行比对。如果一致，说明该文件确实是 Alice 发过来的（因为别人无法拥有 Alice 的私钥），并且文件内容没有被修改过（摘要结果一致）。

数字证书

对于非对称加密算法和数字签名来说，很重要的步骤就是公钥的分发。理论上任何人都可以获取到公开的公钥。然而这个公钥文件有没有可能是伪造的呢？传输过程中有没有可能被篡改呢？一旦公钥自身出了问题，则整个建立在其上的的安全性将不复成立。

数字证书机制正是为了解决这个问题，它就像日常生活中的证书一样，可以确保所记录信息的合法性。比如证明某个公钥是某个实体（个人或组织）拥有，并且确保任何篡改都能被检测出来，从而实现对用户公钥的安全分发。根据所保护公钥的用途，数字证书可以分为加密数字证书（Encryption Certificate）和签名验证数字证书（Signature Certificate）。前者往往用于保护用于加密用途的公钥；后者则保护用于签名用途的公钥。两种类型的公钥也可以同时放在同一证书中。

一般情况下，证书需要由证书认证机构（Certification Authority，CA）来进行签发和背书。权威的商业证书认证机构包括 DigiCert、GlobalSign、VeriSign 等。用户也可以自行搭建本地CA 系统，在私有网络中进行使用。

Merkle 树结构

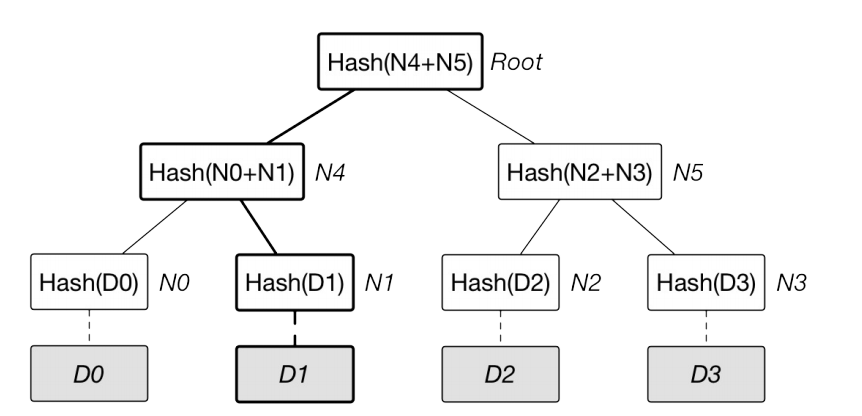
默克尔树（又叫哈希树）是一种典型的二叉树结构，由一个根节点、一组中间节点和一组叶节点组成。默克尔树最早由 Merkle Ralf 在 1980 年提出，曾广泛用于文件系统和 P2P 系统中。

其主要特点为：

• 最下面的叶节点包含存储数据或其哈希值。
• 非叶子节点（包括中间节点和根节点）都是它的两个孩子节点内容的哈希值。

进一步地，默克尔树可以推广到多叉树的情形，此时非叶子节点的内容为它所有的孩子节点的内容的哈希值。

默克尔树逐层记录哈希值的特点，让它具有了一些独特的性质。例如，底层数据的任何变动，都会传递到其父节点，一层层沿着路径一直到树根。这意味树根的值实际上代表了对底层所有数据的“数字摘要”。

最后

以上就是含蓄灰狼为你收集整理的区块链技术指南学习笔记2密码学的全部内容，希望文章能够帮你解决区块链技术指南学习笔记2密码学所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。