【48. 贪心（区间选点）】

• 区间选点与最大不相交区间数量代码一样

思路

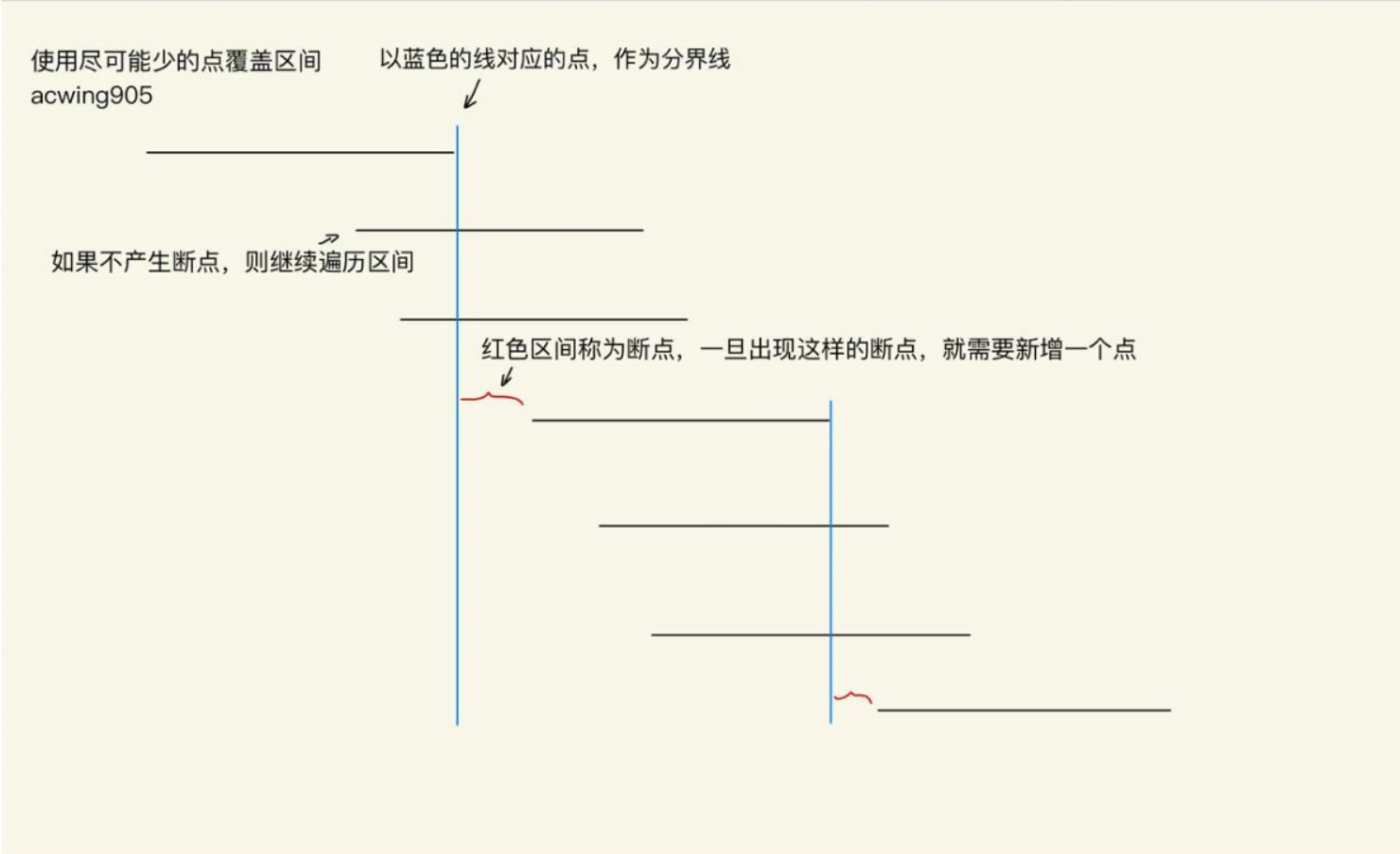
1. 将每个区间按照右端点从小到大进行排序

2. 从前往后枚举区间，end值初始化为无穷小

   • 如果本次区间不能覆盖掉上次区间的右端点， ed < range[i].l,说明需要选择一个新的点， res ++ ; ed = range[i].r;
     
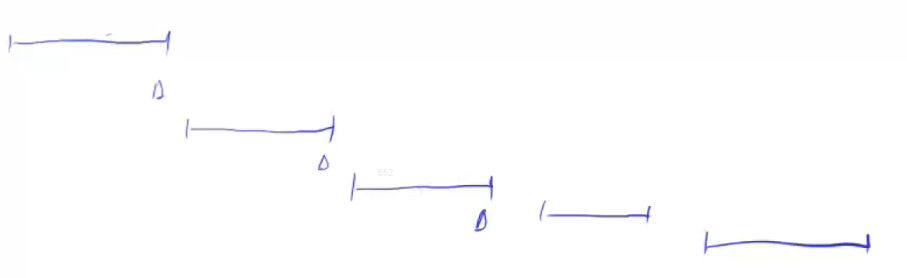
   • 如果本次区间可以覆盖掉上次区间的右端点，则进行下一轮循环

时间复杂度 O(nlogn)O(nlogn)
证明

1. 证明ans<=cnt ：cnt 是一种可行方案， ans是可行方案的最优解，也就是最小值。
2. 证明ans>=cnt ： cnt可行方案是一个区间集合，区间从小到大排序，两两之间不相交。

所以覆盖每一个区间至少需要cnt个点。

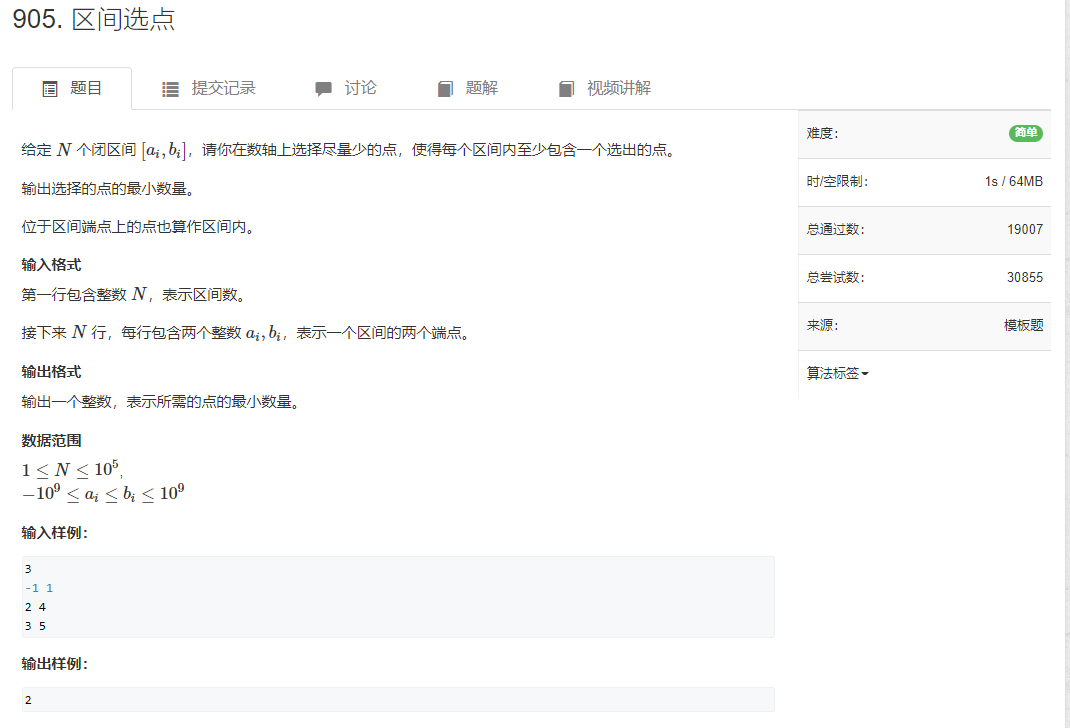
题目

代码

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 100010;
int n;
struct Range
{
  int l, r;      //把区间存进来
  bool operator< (const Range &w) const
  {
      return r < w.r;
  }
}range[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++)
    {
        int l, r;
        scanf("%d%d", &l, &r);
        range[i] = {l, r};
    }
    sort(range, range + n);
    
    //从左往右扫描
     //res表示当前点选择的数量,ed表示上一个点的下标，最开始一个点都没有选择，可以把上一个点赋成负无穷
    int res = 0, ed = -2e9;
    for (int i = 0; i < n; i ++)
        if (range[i].l > ed) //当前点的左端点大于上一个点的右端点，说明有重合
        {
            res ++;
            ed = range[i].r;  //更新
        }
    cout << res;   
    return 0;
}

最后

以上就是听话短靴为你收集整理的【48. 贪心（区间选点）】的全部内容，希望文章能够帮你解决【48. 贪心（区间选点）】所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。