0 总结

学习时间：2022.9.5 ~ 2022.9.11

• 学习了多变量的线性回归的公式表达、梯度下降方法，以及如何进行特征缩放，如何选择学习率。
• 学习了多变量的线性回归的另一种求解参数的方法——正规方程，以及正规方程中不可逆的情况的求解方法。
• 比较了梯度下降和正规方程两种方法的优劣，学会在何种情况下使用何种方法的诀窍。
• 复习了matlab对数据的基本操作，包括：矩阵的运算、切片、绘图等等，还复习了while、for语句的语法、函数的编写方法。
• 学习如何用向量代替循环，从而使运算速度加快。

1 多变量线性回归

1.1 多维特征

变量写法及定义

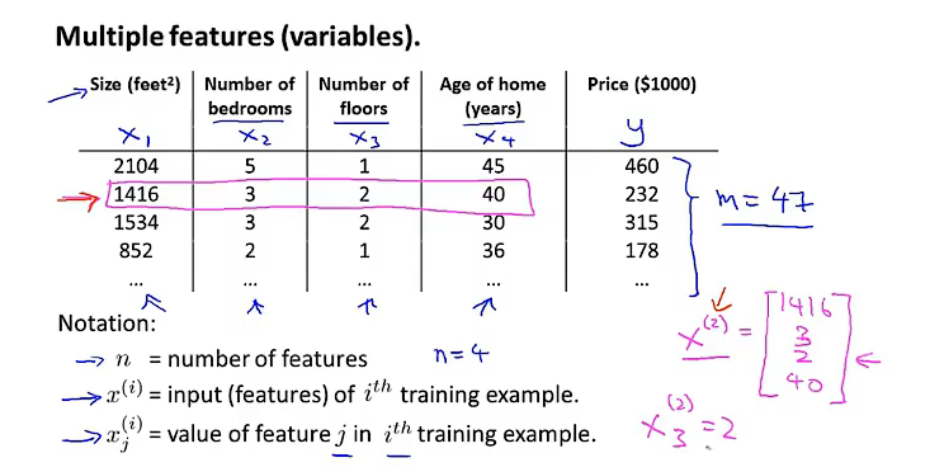
$n$=特征的数量，比如这个例子中，有4个特征（四列）——房子大小($x_1$)、卧室数量($x_2$)、有几层($x_3$)、房子使用时间($x_4$)。
$m$=样本大小，比如这个例子中，有47行，47个样本
$x^{(i)}$=样本的第i个输入，如图中粉色线条所示，$x^{(2)}=\left[\begin{array}{c}1416\\ 3\\ 2\\ 40\end{array}\right]$
$x_j^{(i)}$=第i个输入的第j个特征，$x_3^{(2)}$=2

多元线性回归表达式

1.2 多元梯度下降

从上到下依次是：
假设函数
参数：n+1维向量
代价函数
梯度下降法

左侧是之前推倒的只有一个特征的梯度下降方法。
右侧是多元线性规划的梯度下降方法，注意，$x_0$=1，两者本质上是一样的。

1.3 梯度下降法实践——特征缩放

Q：为什么要进行特征缩放？
A：以房价问题为例，假设我们使用两个特征，房屋的尺寸和房间的数量，尺寸的值为 0-
2000 平方英尺，而房间数量的值则是 0-5，以两个参数分别为横纵坐标，绘制代价函数的等高线图能， 看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛（因为梯度下降走得路径很曲折）。解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。

归一化（mean mormalization）
$$x_n^{(i)}=\frac{x_n^{(i)}-u_n}{s_n}$$其中，$u_n$是平均值，$s_n$是标准差，也可以用最大值-最小值代替。这样算得的x会在-0.5到0.5之间。

1.4 梯度下降法实践——学习率

Q：如何判断梯度下降已经收敛了？
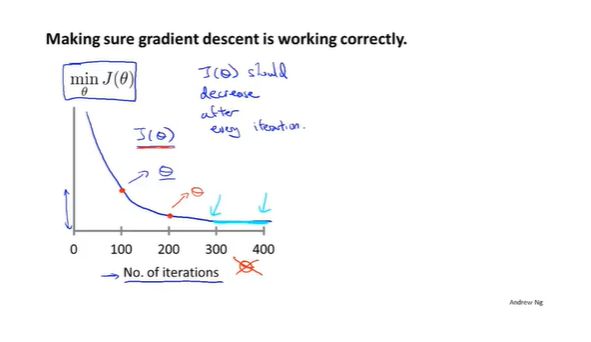
A：在进行迭代的过程中画出下面的图，横坐标表示迭代次数，纵坐标表示对应的$J(\theta )$的值。在每次迭代之后$J(\theta )$应该不断减小。可以看到，第300次迭代和第400次迭代$J(\theta )$的值都差不多，因此可以选择迭代300次。（另：也可以在每次迭代后判断$J(\theta )$是否小于某个很小的数比如$10^{-3}$来判断收敛。但是这个很小的数不好取值）

学习率$\alpha$的选择
$\alpha$太小：收敛慢
$\alpha$太大：$J(\theta )$在每次迭代不一定会减小，甚至不会收敛
解决方法：尝试不同的学习率（…，0.001，0.01，0.1，1，…），通过观察$J(\theta )$曲线判断学习率是否可行。

1.5 特征和多项式回归

1.6 正规方程

到目前为止，我们都在使用梯度下降算法，但是对于某些线性回归问题，正规方程方法
是更好的解决方案。
正规方程是通过求解下面的方程来找出使得代价函数最小的参数的：
$$\frac{\partial J({\theta }_j)}{\partial {\theta }_j}=0$$
假设有m个训练样本$(x^{(1)},y^{(1)}),...,(x^{(m)},y^{(m)})$；n个特征，则：
$$x^{(i)}=\left[\begin{array}{c}{x}_0^{(i)}\\ x_1^{(i)}\\ x_2^{(i)}\\ ⋮\\ x_n^{(i)}\end{array}\right]$$，$x^{(i)}$表示第i个输入样本，是n+1维向量。则：
$$X=\left[\begin{array}{c}(x^{(1)}{)}^T\\ (x^{(2)}{)}^T\\ (x^{(3)}{)}^T\\ ⋮\\ (x^{(m)}{)}^T\end{array}\right]$$，X是$m\times (n+1)$的设计矩阵。利用正规方程解出向量$$\theta =(X^{T}X{)}^{-1}{X}^{T}y$$。
以下表示数据为例：

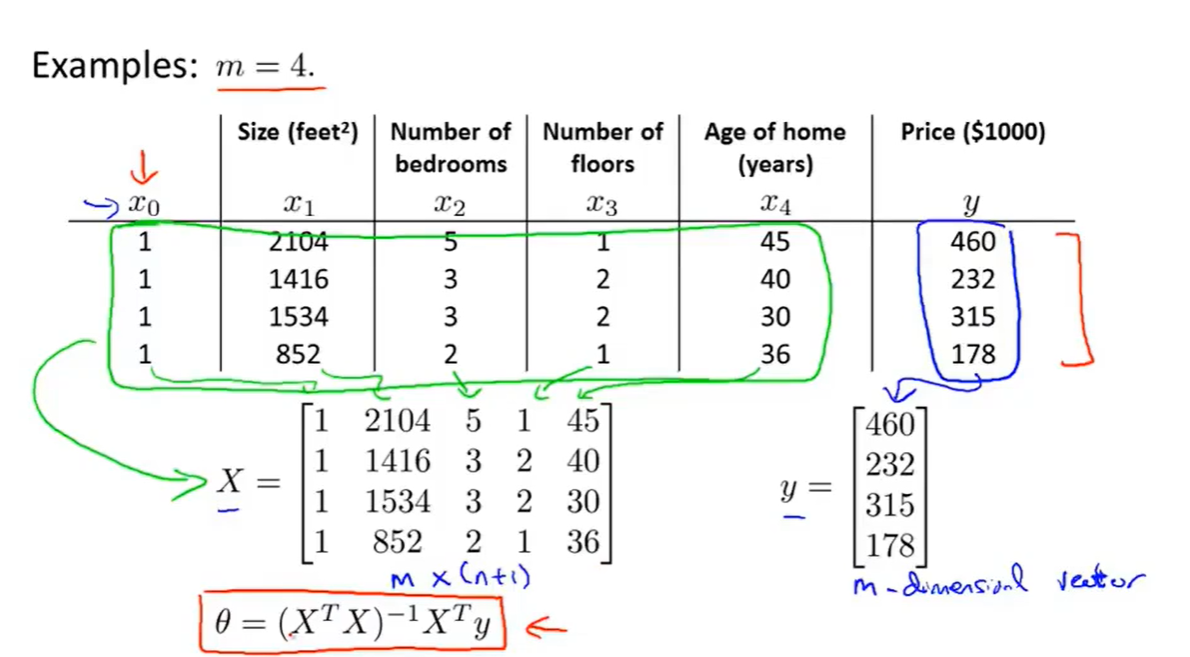
如图，每一列表示特征，每一行表示每个样本，一共4个样本，即m=4，n=4。
由此得到训练集特征矩阵为$X$（包含了$x_0=1$），并且训练结果为$y$，利用正规方程解出向量$\theta =(X^{T}X{)}^{-1}{X}^{T}y$。

Q：什么时候用正规方程法，什么时候用梯度下降？
A：特征个数小于10000时可以选择使用正规方程法。

1.7 正规方程及不可逆性

Q：什么时候$X{X}^T$会不可逆？
A：①特征多余——删除多余的特征
②特征数远大于样本数（$n\ge m$）——删除部分的特征或正则化

2 Octave教程

2.1 基本操作

2.2 移动数据

size
假设A是一个3x2的矩阵，size(A)返回的是[3 , 2]；size(A,1)将返回3，即A的第一个维度；size(A,2)将返回2，即A的第二个维度。

length
假设有一个向量v=[1 2 3 4]， length(v)返回4；length(A)返回3，因为A最大维度是3。

读取和储存数据
载入数据：load(‘featureX.dat’)
删除某个变量：clear featuresX
将变量v储存在hello.mat文件中：save hello.mat v || save hello.txt v -ascii（将数据v以askii码形式存储在hello.txt中）

操作数据
！矩阵索引从1开始
假设$A=\left[\begin{array}{cc}1& 2\\ 3& 4\\ 5& 6\end{array}\right]$

2.3 计算数据

初始化：
$$A=\left[\begin{array}{cc}1& 2\\ 3& 4\\ 5& 6\end{array}\right],B=\left[\begin{array}{cc}11& 12\\ 13& 14\\ 15& 16\end{array}\right],C=\left[\begin{array}{cc}1& 1\\ 2& 2\end{array}\right],V=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$$

2.4 绘图

绘制$sin(8\pi t)$和$cos(8\pi t)$

t=[0:0.01:0.98]; % t=[0,0.01,0.02,...,0.98]
y1=sin(2*pi*4*t);
y2=cos(2*pi*4*t);
plot(t,y1);
hode on; % 将新的图像绘制在旧的之上
plot(t,y2);
xlabel('time');ylabel('value'); % 标记x轴和y轴
legend('sin','cos') % 图例放在右上方
title('myplot'); % 显示标题

可视化矩阵

%% 生成一个颜色图像， 一个灰度分布图， 并在右边也加入一个颜色条。 
%% 所以这个颜色条显示不同深浅的颜色所对应的值
A=magic(5)
imagesc(A)
colorbar
colormap gray

2.5 控制语句

for语句

v = zeros(10,1);
for i=1:10, % i=1，i=2，...，i=10
	v(i)=2^i;
end;

while语句

i=1；
while true,
	v(i) = 999;
	i=i+1;
	if(i==6)
		break; % i=6时停止循环
	end; % 结束if语句
end; % 结束while语句

if-else语句

if v(1)==1,
	disp('value = 1');
elseif v(1)==2,
	disp('value = 2');
else
	disp('value unknow');
end;

函数
定义的squarethisnumber函数保存在squarethisnumber.m中。

function y = squareThisNumber(x) % 函数需要输入一个参数x，函数返回的值保存在y中
	y=x^2;

复杂一点的例子（计算损失函数）：

function J = costFunction(X, y, theta)
	% X 包含训练集的设计矩阵
	% y 是分类标签
	m = size(X,1);            % 训练集的个数（也就是X的行数）
	predictions = X*theta;    % 预测值，m维的向量
	sqrError = (predictions - y).^2
	J = 1/(2*m)*sum(sqrErrors); 

2.6 向量化

以之前的线性规划为例子

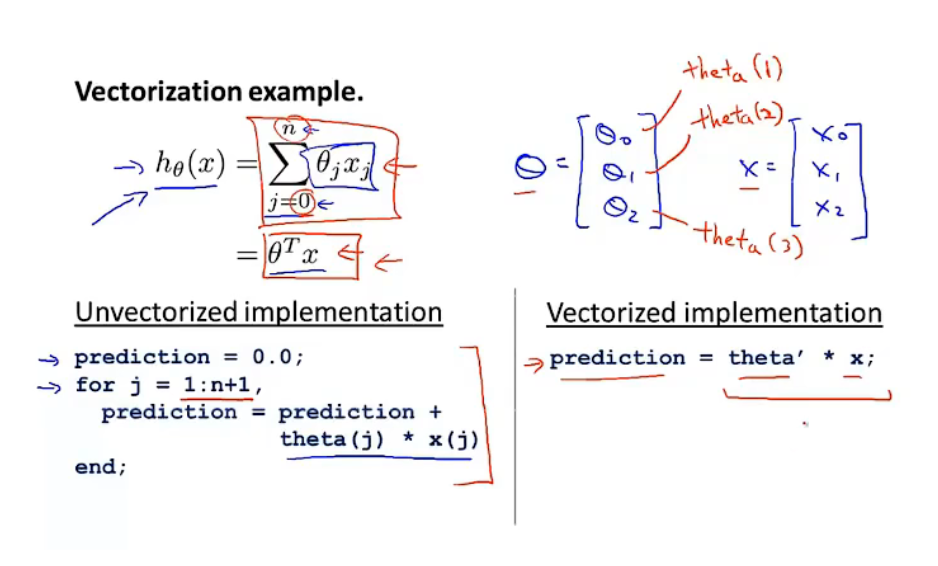
左侧为没有向量化的表达，因为matlab中矩阵下标从1开始，所以j是从1到n+1。
右侧为向量化的表达。

梯度下降

$\theta$是每个特征前的参数。
假设有m个训练样本$(x^{(1)},y^{(1)}),...,(x^{(m)},y^{(m)})$；n个特征，则：
$$x^{(i)}=\left[\begin{array}{c}{x}_0^{(i)}\\ x_1^{(i)}\\ x_2^{(i)}\\ ⋮\\ x_n^{(i)}\end{array}\right]$$，$x^{(i)}$表示第i个输入样本，是n+1维向量。则：
$$X=\left[\begin{array}{cccc}{x}_0^{(1)}& x_1^{(1)}\cdots & x_n^{(1)}& \\ x_0^{(2)}& x_1^{(2)}\cdots & x_n^{(2)}& \\ x_0^{(3)}& x_1^{(3)}\cdots & x_n^{(3)}& \\ ⋮& ⋮& ⋮& \\ x_0^{(m)}& x_1^{(m)}\cdots & x_n^{(m)}& \end{array}\right]$$，X是$m\times (n+1)$的设计矩阵。

最后

以上就是甜美月光为你收集整理的吴恩达ML WEEK2 线性回归+MATLAB0 总结1 多变量线性回归2 Octave教程的全部内容，希望文章能够帮你解决吴恩达ML WEEK2 线性回归+MATLAB0 总结1 多变量线性回归2 Octave教程所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。