数学建模学习-插值法

插值：在平面上给定一组离散点列，要求一条曲线，把这些点按次序连接起来，成为插值。

Matlab插值工具：

1.一维插值函数

Matlab现成的一维插值函数为interp1。语法为

y = interp1(x0,y0,x,'method')

x0和y0分别为离散的点的横坐标和纵坐标。x通常为坐标轴范围如x = 10 :10:100

methond为指定插值的方法，默认为线性插值。可以为

'nearest' 最近项插值

'linear' 线性插值

‘spline' 立方样条插值

'cubic' 立方插值

其中，所有的插值方法都要求x0是单调数列。

2.三次样条插值

Matlab中三次样条插值有如下函数

y = interp1(x0,y0,x,'spline');
y = spline(x0,y0,x);
pp = csape(x0,y0,conds); y = fnval(pp,x);
pp = csape(x0,y0,conds,valconds);y = fnval(pp,x);

对于三次样条插值，通常使用csape函数。其返回值为pp形式，要获得插值点函数值，必须调用fnval函数。

pp = csape(x0,y0)使用默认的边界条件，即Lagrange边界条件。

pp = csape(x0,y0,conds,valconds)中的conds的指定插值的边界条件，其值可为：

'complete' 边界为一阶导数，一阶导数的值在valconds参数中给出，若忽略valconds参数视为默认情况。

'second' 边界为二阶导数，二阶导数的值在参数valconds中给出，不使用参数valconds，默认值为[0,0]。

例：

对以上数据进行插值处理：

分别使用最临近插值法，立方样条插值的不同边界得到的结果。

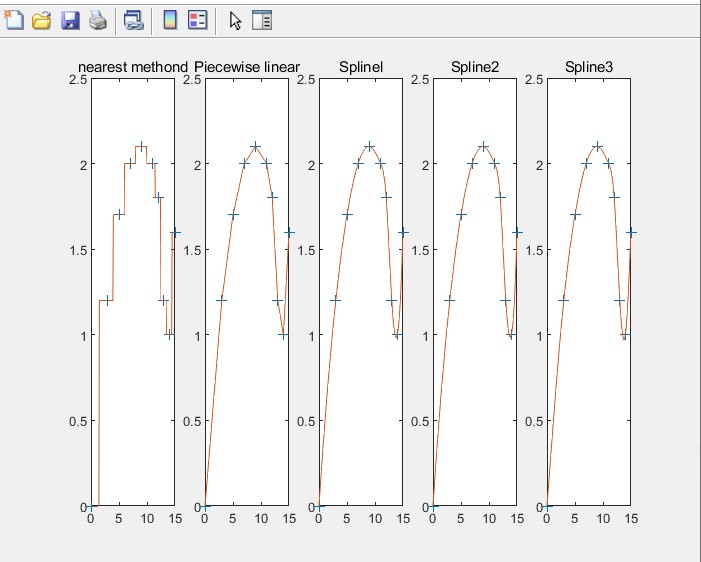
 从图中可以看出三次样条插值得到的曲线更平滑。

Matlab代码如下

x0=[0 3 5 7 9 11 12 13 14 15];
y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];
x=0:0.1:15;
y6 = interp1(x0,y0,x,'nearest');
subplot(1,5,1)
plot(x0,y0,'+',x,y6);
title('nearest methond');
y1 = interp1(x0,y0,x); %x和y的坐标，坐标轴
y2 = interp1(x0,y0,x,'spline');
pp1 = csape(x0,y0);
y3 = fnval(pp1,x);
pp2 = csape(x0,y0,'second');
y4 = fnval(pp2,x);  %使用fnval函数求插值点的函数值
subplot(1,5,2)
plot(x0,y0,'+',x,y1);
title('Piecewise linear');
subplot(1,5,3)
plot(x0,y0,'+',x,y2)
title('Splinel')
subplot(1,5,4)
plot(x0,y0,'+',x,y3)
title('Spline2')
subplot(1,5,5)
plot(x0,y0,'+',x,y4);
title('Spline3')

2.二维插值

1）插值节点为网格节点

Matlab中有计算二维插值的命令

z = interp2(x0,y0,z0,x,y,'method')

x0,y0分别为m维和n维向量，表示节点;z0维mxn矩阵，表示节点值，x,y维一维数组，表示插值点。method和一维插值的参数相同。

如果是三次样条插值，可以使用命令

pp = csape({x0,y0},z0,conds,valconds);
z = fnval(pp,{x,y});

2）插值点是散乱的点

Matlab提供了插值函数griddata

ZI = griddata(x,y,z,XI,YI);

x,y,z均为n维向量，指出横坐标，纵坐标和竖坐标。XI YI是给定网格点的横坐标和纵坐标，返回值ZI是网格（XI,YI）处的函数值。XI,YI应是方向不同的向量。

应用示例：

clc,clear
x = [129,140,103.5,88,185.5,195,105,157.5,107.5,77,81,162,162,117.5];
y = [7.5,141.5,23,147,22.5,137.5,85.5,-6.5,-81,3,56.5,-66.5,84,-33.5];
z = -[4,8,6,8,6,8,8,9,9,8,8,9,4,9];
xmm = minmax(x) %求最大最小值
ymm = minmax(y)
xi = xmm(1):xmm(2);
yi = ymm(1):ymm(2);
zi1 = griddata(x,y,z,xi,yi','cubic'); %立方插值,y'使xi与yi方向不同
zi2 = griddata(x,y,z,xi,yi','nearest'); %最近点插值
zi = zi1;                          %采用混合插值的方式，先用zi1初始化结果
zi(isnan(zi1)) = zi2(isnan(zi1))   %把立方插值中不确定nan的值换成最近点插值的结果
subplot(1,2,1);
plot(x,y,'*')
subplot(1,2,2);
mesh(xi,yi,zi)                      %绘图

结果如图：

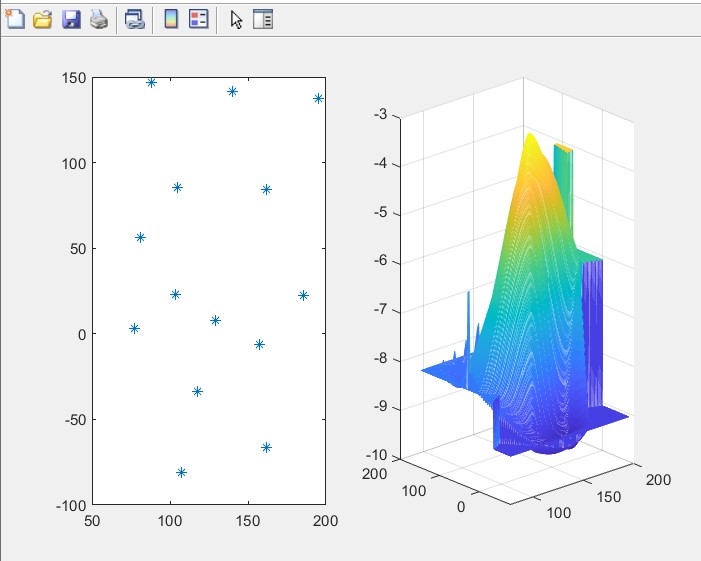
最后

以上就是俏皮背包为你收集整理的数学建模学习-插值法的全部内容，希望文章能够帮你解决数学建模学习-插值法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。