无线通信原理笔记3

92 阅读 0 评论 61 点赞

我是靠谱客的博主忐忑犀牛，最近开发中收集的这篇文章主要介绍无线通信原理笔记3，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

MIMO系统

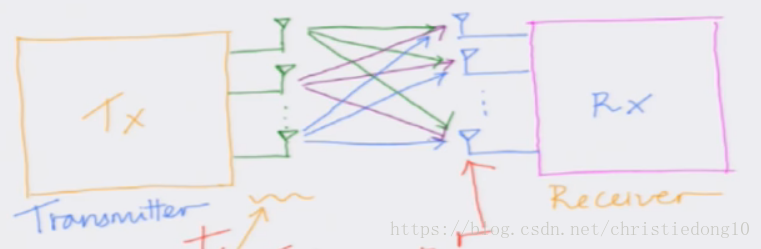
前面已经看到，使用多个接收天线进行最大比合并可以获得最大的接收信噪比，也就是通过分集提高系统的可靠性。

进一步，在发端也使用多个天线，可以构成多输入多输出系统（MIMO），它可以在空间维度上并行传输多个信息流，从而大大提高系统的传输速率——空间复用（Spatial Multiplexing）。

假设MIMO系统的发端有t个天线，收端有r个天线，在t个发射天线上发送的符号为(mathbf{x}=[x_1 x_2 cdots x_t]^T)，r个接收天线上接收的信号为(mathbf{y}=[y_1 y_2 cdots y_r]^T)，收发天线之间的无线信道则可以建模为

$$mathbf{H}=[h_{ij}]_{rtimes t}=begin{bmatrix} h_{11}& h_{12} & cdots & h_{1t}\ h_{21}& h_{22} & cdots & h_{2t}\ vdots& vdots & &vdots \ h_{r1}& h_{r2} & cdots & h_{rt} end{bmatrix}$$

其中(h_{ij})是第(j)根发射天线与第(i)根接收天线之间的信道增益系数。

由此，MIMO系统可以建模为

$$mathbf{y}=mathbf{H}mathbf{x}+mathbf{w}$$

其中(mathbf{w}=[w_1 w_2 cdots w_r]^T)是r个接收天线上收到的噪声信号，每个元素均可建模为相互独立同分布（iid）的随机变量，且服从零均值的高斯分布，即(w_i sim N(0,sigma^2))，且

$$E{w_iw_j^*}=left{ begin{matrix} sigma^2, & operatorname{if} i=j \ 0, & operatorname{else} end{matrix}right.$$

考察(mathbf{w})的协方差矩阵，得到

$$begin{aligned} E{mathbf{w}mathbf{w}^H}=Eleft{ begin{bmatrix} |w_1|^2 & w_1w_2^* & cdots & w_1w_r^* \ w_2w_1^* & |w_2|^2 & cdots & w_2w_r^* \ vdots & vdots & & vdots \ w_rw_1^* & w_rw_2^* & cdots & |w_r|^2 end{bmatrix}right}=begin{bmatrix} E{|w_1|^2}&0&cdots& 0 \ 0& E{|w_2|^2} & cdots & 0 \ vdots & vdots & ddots& vdots \ 0 & 0& cdots & E{|w_r|^2}end{bmatrix} &=sigma^2mathbf{I}_rend{aligned}$$

MIMO接收机

假设t发r收的MIMO系统的系统模型为

$$mathbf{y}=mathbf{H}mathbf{x}+mathbf{w}$$

那么，如何才能从接收向量(mathbf{y})中恢复发送向量(mathbf{x})呢？我们来讨论MIMO系统的最佳接收机——Zero Forcing（ZF）接收机。

当接收天线数与发送天线数相同，即(r=t)时，信道矩阵(mathbf{H})是方阵。更进一步，如果其逆矩阵存在，记为(mathbf{H}^{-1})，我们可以使用信道矩阵的逆矩阵来处理接收向量，进而得到发送向量的估计，即

$$hat{mathbf{x}}=mathbf{H}^{-1}mathbf{y}$$

然而，很多情况下，收发天线不相同，信道矩阵的逆矩阵也就不存在，怎么办？

考虑一种特殊情况，假设接收天线比发送天线多，即(r>t)，此时系统模型中等式的个数（等于接收天线数）比未知数的个数（等于发送天线数）多，因此方程组不一定有解，即不一定存在一组x使得所有的等式都满足。但是，我们可以得到一组近似的解，尽量满足所有的约束。

定义一个误差向量(mathbf{e}=mathbf{y}-mathbf{H}mathbf{x})，它表示用我们估计的发送向量与信道的乘积与接收向量之间的差别，我们选取估计的发送向量，使得这个误差的功率最小，此时的估计量就是最优的。这一优化问题可以描述为

$$hat{mathbf{x}}=operatorname{argmin}{left| mathbf{y}-mathbf{Hx} right|^2}$$

其中，目标函数定义为

$$begin{aligned} F(mathbf{x})&=left| mathbf{y}-mathbf{Hx} right|^2 \ &=(mathbf{y}-mathbf{Hx})^T(mathbf{y}-mathbf{Hx}) \ &=mathbf{y}^Tmathbf{y}-mathbf{x}^Tmathbf{H}^Hmathbf{y}-mathbf{y}^Tmathbf{H}mathbf{x}+mathbf{x}^Tmathbf{H}^Tmathbf{H}mathbf{x} end{aligned}$$

对于功率值来说，(mathbf{x}^Tmathbf{H}^Hmathbf{y}=mathbf{y}^Tmathbf{H}mathbf{x})，因此

$$F(mathbf{x})=mathbf{y}^Tmathbf{y}-2mathbf{x}^Tmathbf{H}^Tmathbf{y}+mathbf{x}^Tmathbf{H}^Tmathbf{H}mathbf{x}$$

上述估计方法称为最小二乘估计（Least Square, LS）。

求解上式的方法需要对目标函数求导，并置导数为零后求解最优的估计量，即求解

$$frac{partial F(mathbf{x})}{partial x}=0$$

再具体求解之前，我们先复习向量求导的几个结论。

对于n维向量(mathbf{c})和(mathbf{x})来说，当(F(mathbf{x})=mathbf{c}^Tmathbf{x}=c_1x_1+c_1x_1+cdots+c_nx_n)时，

$$begin{aligned} frac{partial F(mathbf{x})}{partial mathbf{x}}&= left[frac{partial F(mathbf{x})}{partial x_1},frac{partial F(mathbf{x})}{partial x_2},cdots,frac{partial F(mathbf{x})}{partial x_n} right]^T \ &=[c_1,c_2,cdots,c_n]^T =mathbf{c} end{aligned}$$

当(F(mathbf{x})=mathbf{x}^Tmathbf{c}=x_1c_1+x_1c_1+cdots+x_nc_n)时，

$$frac{partial F(mathbf{x})}{partial mathbf{x}}=mathbf{c}$$

因此，得到如下结论

$$frac{partial mathbf{c}^Tmathbf{x}}{partial mathbf{x}}=frac{partial mathbf{x}^Tmathbf{c}}{partial mathbf{x}}=mathbf{c}$$

除此之外，考虑二次函数的形式，即(F(mathbf{x})=mathbf{x}^Tmathbf{P}mathbf{x})，且满足(mathbf{P}=mathbf{P}^T)则

$$begin{aligned} frac{partial (mathbf{x}^Tmathbf{P}mathbf{x})}{partialmathbf{x}}&=mathbf{Px}+(mathbf{x}^Tmathbf{P})^T \ &=2mathbf{Px} end{aligned}$$

下面来求解上述目标函数(F(mathbf{x})=0)的解

$$frac{partial F(mathbf{x})}{partial mathbf{x}}=0-2mathbf{H}^Tmathbf{y}+2mathbf{H}^Tmathbf{Hx}=0 $$

因此，最优估计量为

$$hat{mathbf{x}}=(mathbf{H}^Tmathbf{H})^{-1}mathbf{H}^Tmathbf{y}$$

当我们拓展到复数向量时，转置操作就变成了共轭转置，即

$$hat{mathbf{x}}=(mathbf{H}^Hmathbf{H})^{-1}mathbf{H}^Hmathbf{y}$$

由于

$$(mathbf{H}^Hmathbf{H})^{-1}mathbf{H}^Hmathbf{H}=mathbf{I}$$

所以，((mathbf{H}^Hmathbf{H})^{-1}mathbf{H}^H)称为(H)的“伪逆”。

由此可知，MIMO系统的最佳接收机（ZF接收机）使用信道矩阵的伪逆来获得发射向量的估计，这一估计量在最小二乘（LS）意义下是最优的。

发射端波束赋形（Beamforming）

我们在SIMO系统中（单发多收）使用最大比合并获得最大的接收信噪比，这实际上是使接收天线阵列的接收方向“对准”发送天线，本质上是一种接收端的波束赋形。类似的，在发送端也可以使用波束赋形将发送的波束“对准”某个方向，这个最优的方向是什么呢？

考虑一个具有2个发射天线和1个接收天线的MISO系统（多发单收）。接收到的信号可以表示为

$$mathbf{y}=[h_1 h_2]begin{bmatrix} x_1 \ x_2 end{bmatrix}+w$$

其中(h_1)和(h_2)是两个发射天线到接收天线之间的信道系数，(mathbf{x}=[x_1, x_2]^T)是两个发射天线上的“发送向量”,(w)是高斯白噪声信号，服从均值为零，方差为(sigma^2)的复高斯分布。

若数据符号(x)按如下方式映射到每个天线上

$$mathbf{x}=frac{1}{left|mathbf{h}right|}begin{bmatrix} h_1^*\h_2^* end{bmatrix}x$$

其中(left|mathbf{h}right|=sqrt{h_1^2+h_2^2})，则向量

$$left[ frac{h_1^*}{left|mathbf{h}right|}, frac{h_2^*}{left|mathbf{h}right|} right]^T$$就是归一化的发射波束赋形矢量。将上述发射矢量(x)代入系统模型中，接收信号为

$$begin{aligned} mathbf{y}&= [h_1 h_2]begin{bmatrix} frac{h_1^*}{left|mathbf{h}right|}x \ frac{h_2^*}{left|mathbf{h}right|}x end{bmatrix}+w \ &=frac{|h_1|^2}{left|mathbf{h}right|}+frac{|h_2|^2}{left|mathbf{h}right|}+w \ &=left|mathbf{h}right|x+w end{aligned}$$

abc