电子技术基础(三)__第5章 之逻辑函数相关的 最小项、卡诺图、逻辑图

逻辑函数的表示形式主要有：  逻辑函数表达式、真值表、卡诺图、逻辑图。

本文主要介绍 逻辑函数表达式里的最小项，卡诺图， 逻辑图。

1 最小项

设由三个输入变量A、B、C组成逻辑函数， 可以组成许多乘积项， 如ABC、 A(B+C)、、等， 其中有一类乘积项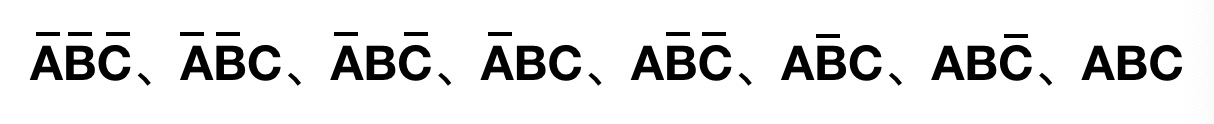：, 这8个乘积项就是三变量输入函数的最小项。

最小项具有以特点：

1.  每个乘积项包括三个输入量；

2. 每个变量都以原变量（A、B、C）或反变量（A、B、C）的形式在每个乘积项中出现且仅出现一次。

表1 列出了三变量所有最小项

ABC	最小项	最小项编号
000		m0
001		m1
010		m2
011		m3
100		m4
101		m5
110		m6
111		m7

                                                               表1   三输入变量所有最小项

对于n个输入变量的逻辑函数，就有  个最小项。

最小项具有下列性质：

• 对于任意一个最小项，只有输入变量的一组取值使得它的值为1.  而取其他值时， 这个最小项的值都为0.
• 对于同一个变量取值， 任意两个最小项的乘积恒为0. 
    即 mi = mj（i    j）
• 任意取值的变量条件下，全体最小项的和为1。
  
  
  以下看几个例子：
  
  例1：  写出二输入变量A、B的最小项。
  
  解：  二输入变量有 4 个最小项， 按照最小项定义， 四个最小项如下：
   

、、、

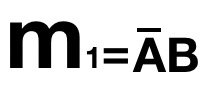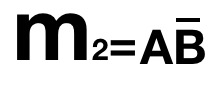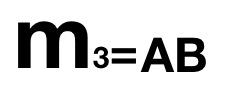
例2：

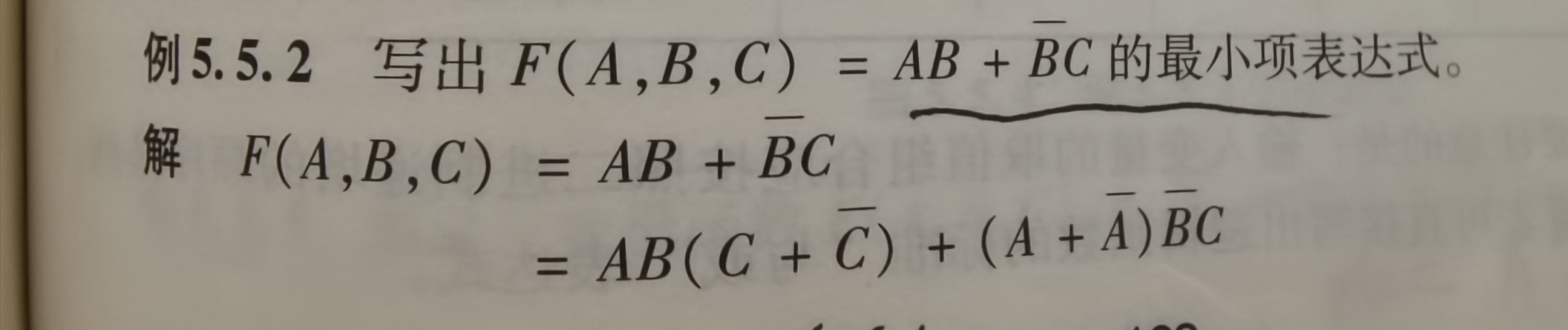
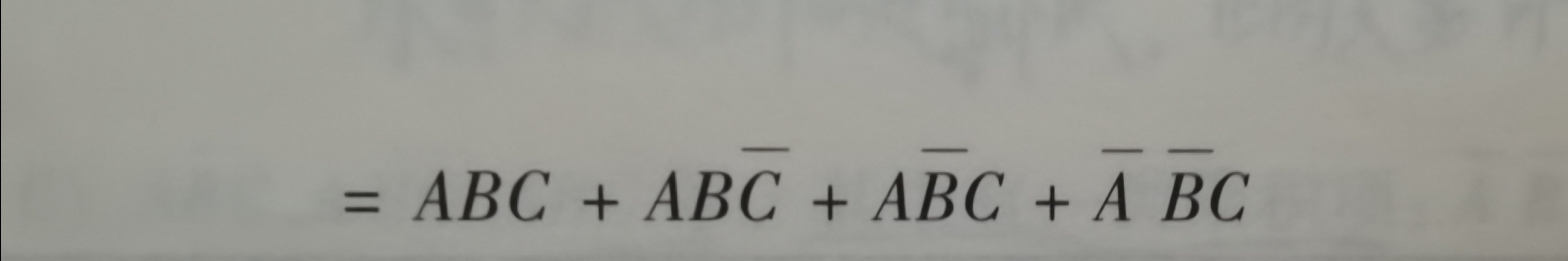
上式的最小项可分别表示为m1、m5、m6、m7， 所以又可写为 F（A，B，C）=m1 + m5 + m6 + m7， 或者

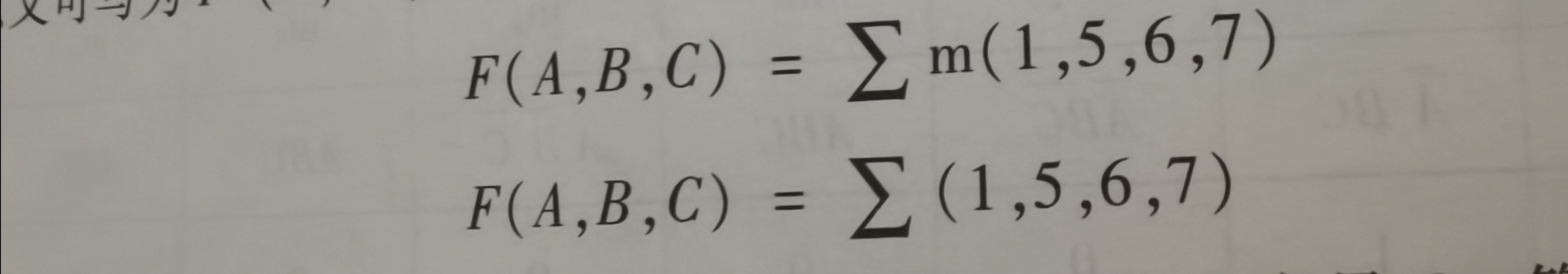
2 卡诺图

卡诺图是图形化的真值表， 是由美国工程师卡诺（Karnaugh）首先提出的一种用来描述逻辑函数的特殊方格图。

2.1  对于具有两个输入变量 A和B的逻辑函数，把输入变量A和B分别横写和竖写， 列出可能的取值0和1， 再把与A和B形成的最小项填入对应的方格中，用这样的表格表示逻辑函数称为卡诺图。

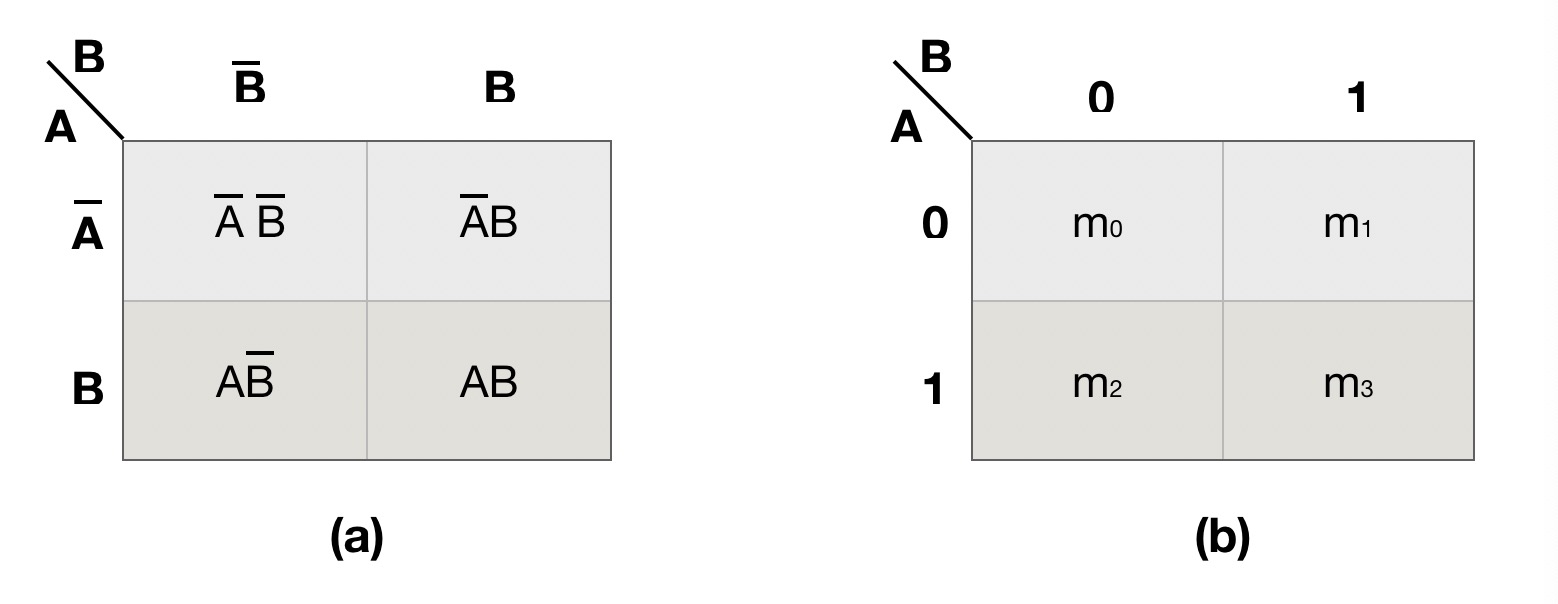
                                 图 1             二变量的卡诺图

图1 中每一个方格对应逻辑函数的一个最小项， 而且几何位置相邻（上下或左右相邻）的小方格具有逻辑相邻性，也就是说两个相邻小方格所代表的最小项只有一个变量取值不同。

2.2 对于有n个变量的逻辑函数， 其最小项有   个，因此该逻辑函数的卡诺图由 个小方格构成， 每个小方格都满足逻辑相邻项的要求。 三变量的卡诺图如下图2 所示， 四变量的卡诺如下图3所示。

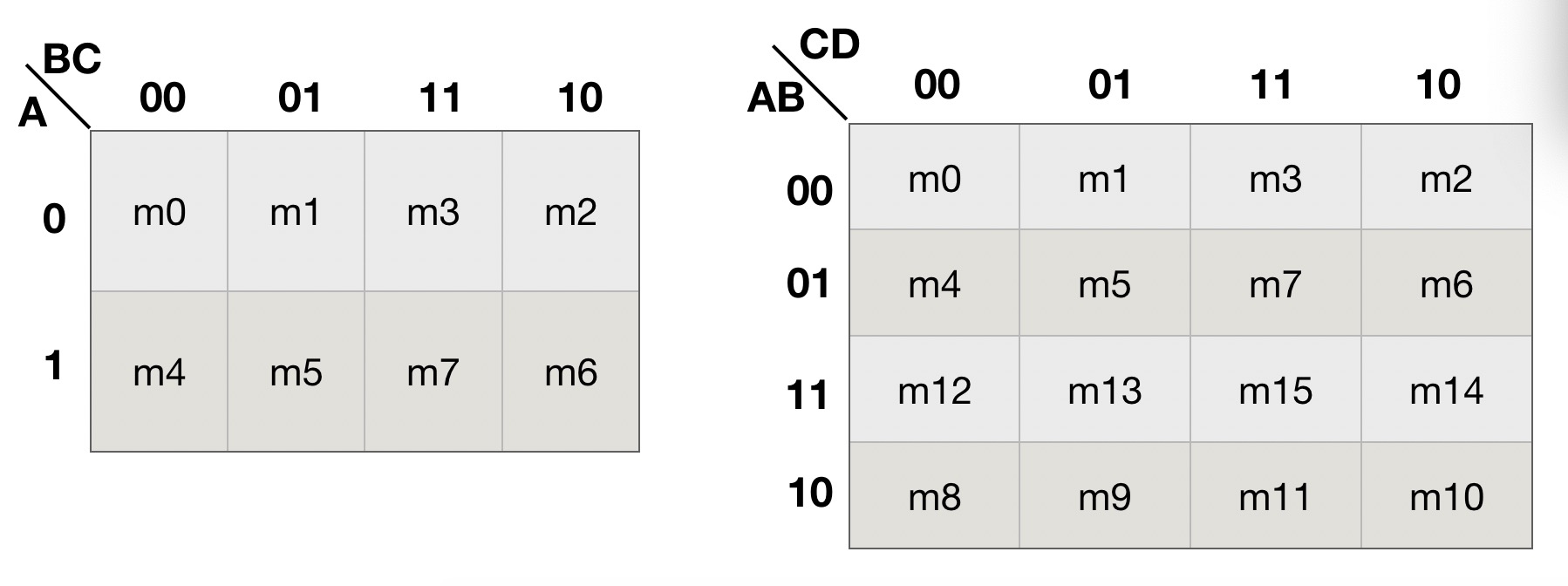
               图2    三变量的卡诺图                                               图3         四变量的卡诺图

注意 卡诺图的顺序， 行的排列是 00， 01，11，10，  因此三变量 第一行后两格是 m3,m2， 不是m2, m3,   注意观察顺序

2.3  以下看几个例子

例1：  画出两变量函数F (A,B) = m(0, 2)的卡诺图。

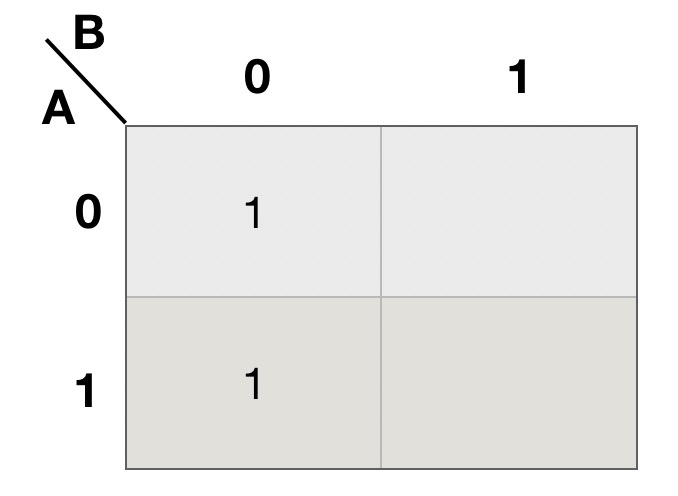
解： 先画出两变量函数卡诺图，也就是有 4 个方格的表格， 再将两个输入变量 A 和 B 分别分配在列和行上，将对应于

m0 =  和 m2 = 的方格填上1.  即下图

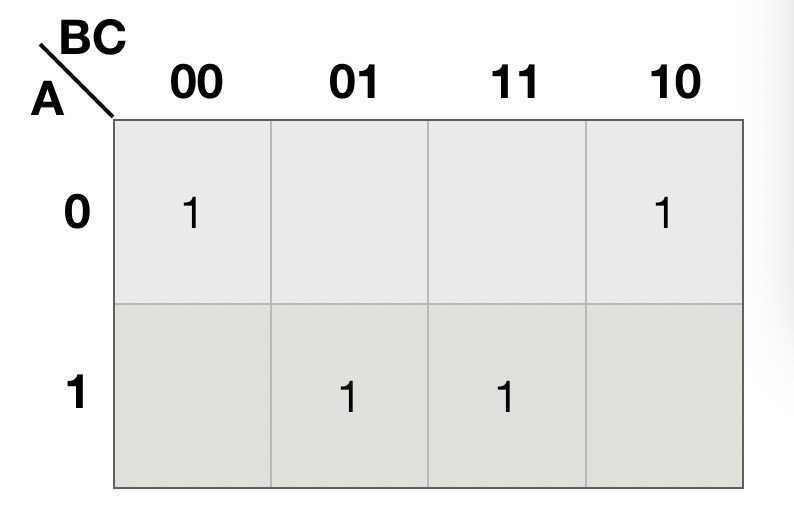
例2： 画出三变量函数F(A,B,C) = m(0, 2, 5, 7)的卡诺图

解：先画出三变量卡诺图， 也就是有8个方格的表格，将变量 A 分配在列， 变量 BC 分配在行上； 列出变量 A的两种可能的取值0和1， 变量BC的四种可能的取值：00、01、11、10， 注意逻辑相邻原则；再将对应于最小项m0、m2、m5、m7的方格填上1，其他的方格不填。

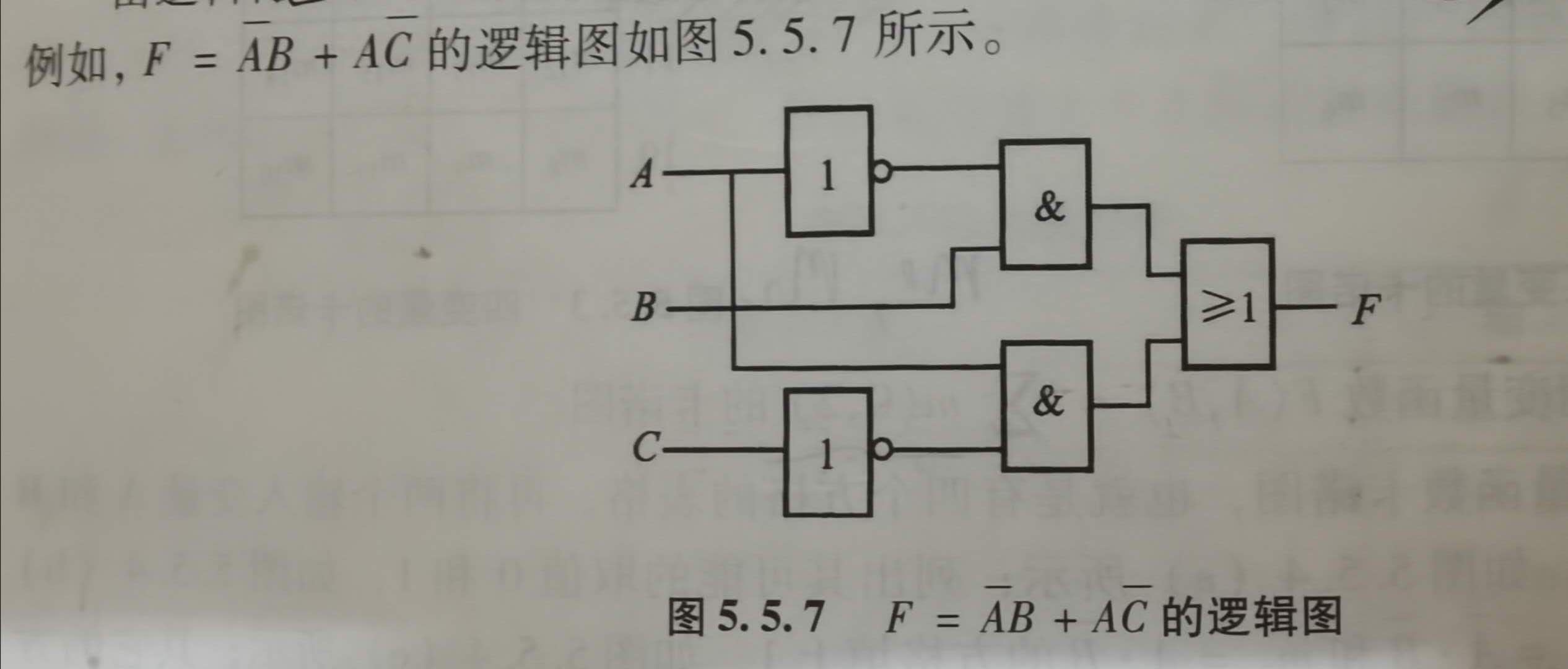
3  逻辑图

由逻辑符号表示逻辑函数的图形， 叫做逻辑电路图， 简称逻辑图。

最后

以上就是难过大地为你收集整理的电子技术基础(三)__第5章 之逻辑函数相关的 最小项、卡诺图、逻辑图的全部内容，希望文章能够帮你解决电子技术基础(三)__第5章 之逻辑函数相关的 最小项、卡诺图、逻辑图所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。