二进制基础：补码，左移，右移

引入

二进制是计算机的基础，追根溯源还是因为Si的半导体性。

除了二进制，还有十六进制，它是简化二进制的表示。

做个测试：

  @Test
    public void testHex() {
        int n = 0x77d45d25;
        System.out.println(
                Integer.toBinaryString(n));
    }

0x表示这是一个十六进制数。

结果：

1110111110101000101110100100101

我们自己转换一下：

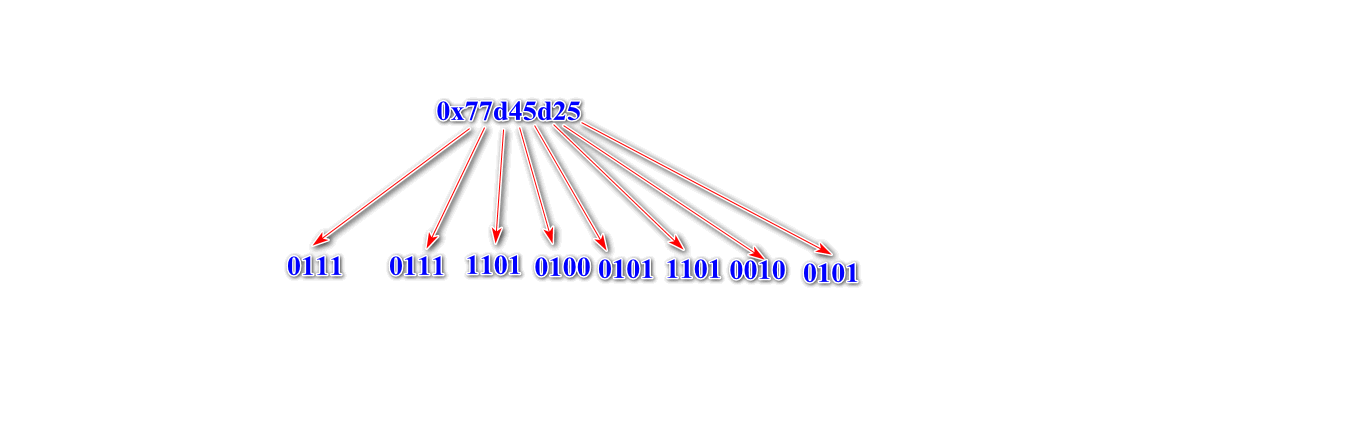
控制台输出的结果它把最高位的0给舍掉了，但这个不影响。

为什么要有补码

先看0000到1111的二进制数：

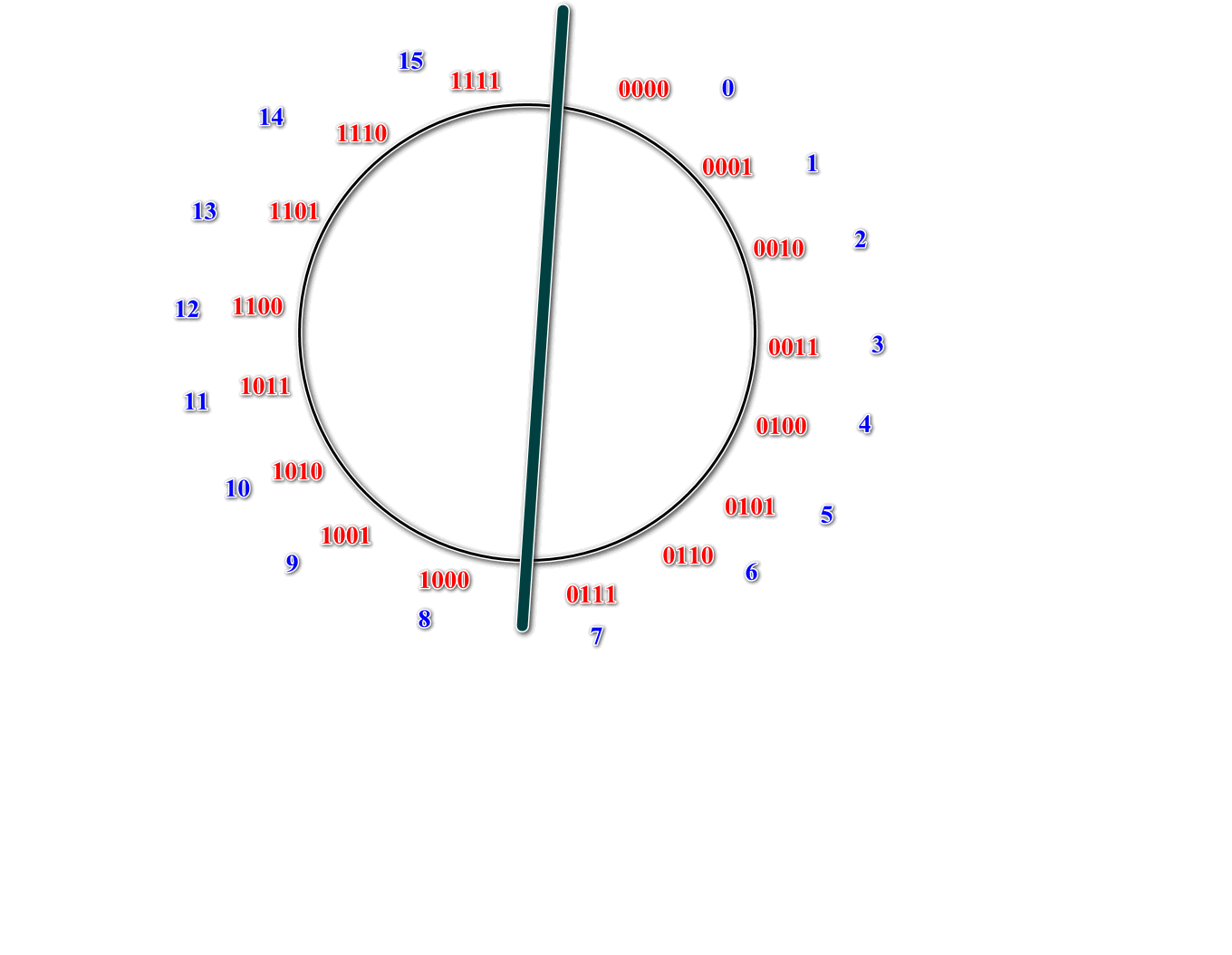
十进制代表的就是0到15。

那这里为什么要画成一个圈呢？因为有溢出的概念。

我们等下会测试。

现在的问题是：怎么才能有负数？

解决的办法就是，把0到15这16个数分一半给负数：

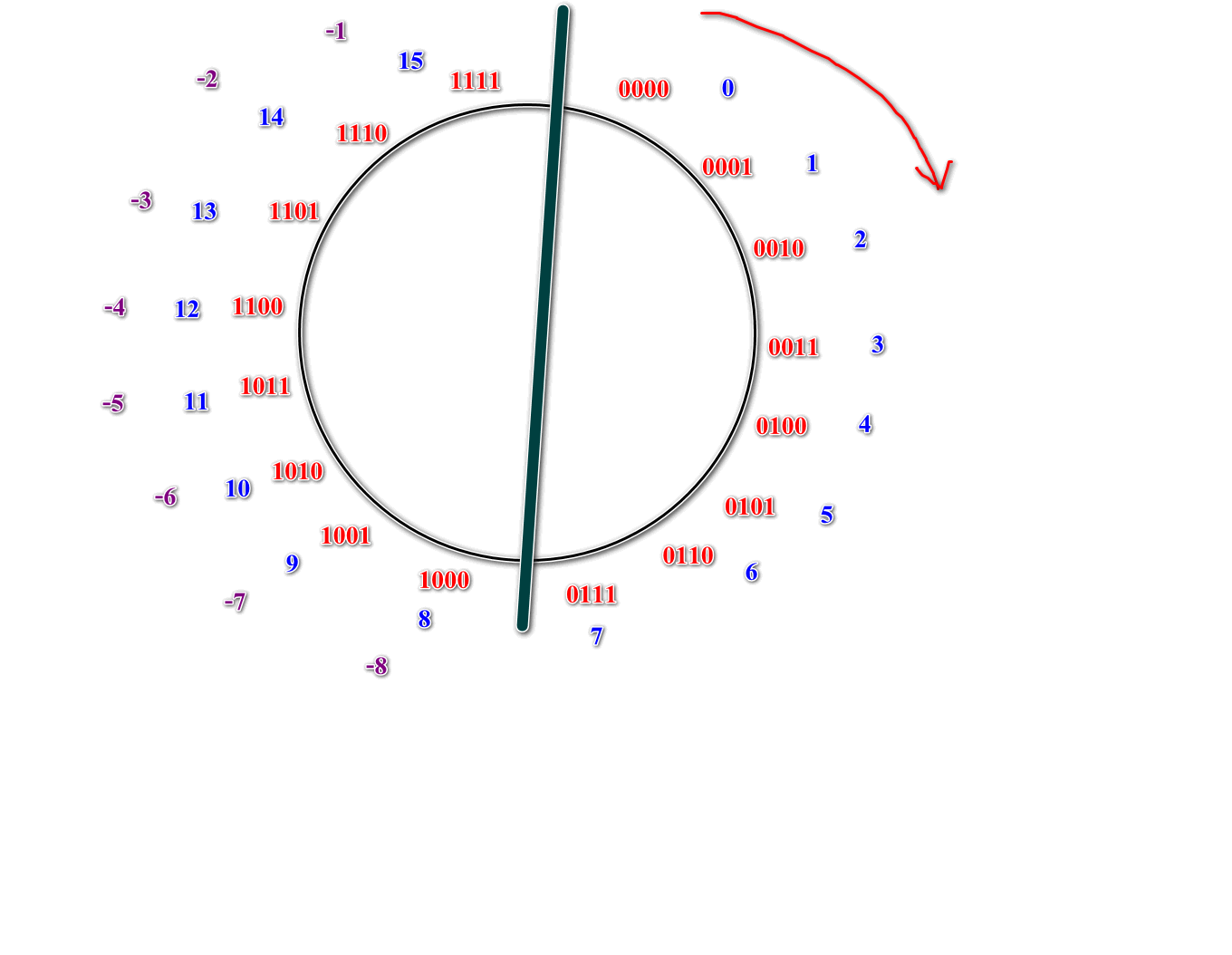
这样就ok了。我们终于有负数了。

这么一划分出现了一个神奇的事情：

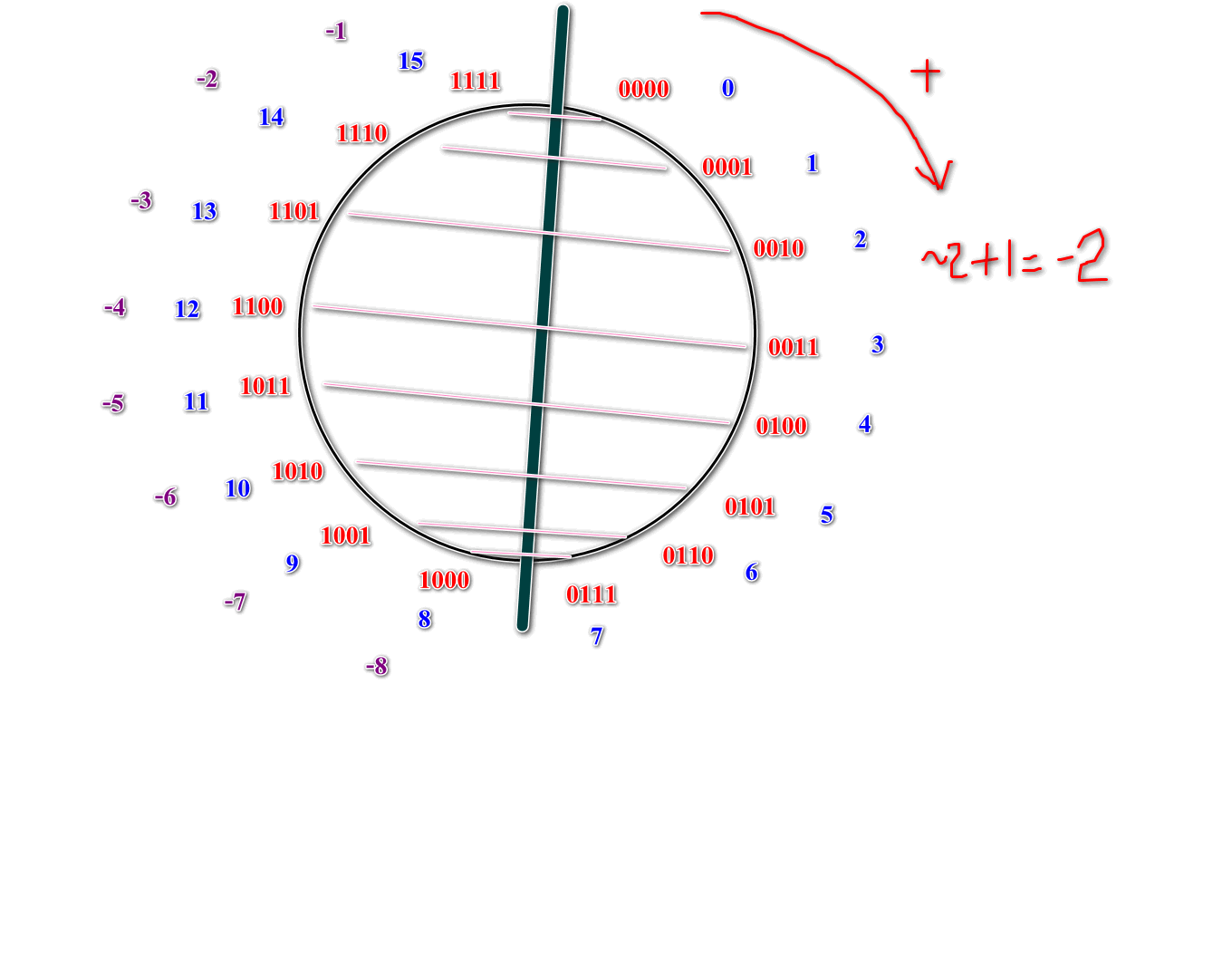
这个圈圈上的任意一个数，它的二进制取反之后，再加一（顺时针移动一次），会变成原数的相反数！

比如2，它的二进制是0010。

取反：1101

加一：1110

在图上看看，1110不就是-2吗？

拿代码测一下：

 @Test
    public void testInverse(){
        System.out.println(~100+1);
    }

结果：

-100

特殊的值

我认为的补码就是因为负数而产生的。

我们观察上面的图，注意几个特别的数：

在四位的情况下：

0—>0000
-1—>1111
最小值 —> 1000
最大值 —> 0111

你需要记住的是，任何位数，-1永远都是一群1。

    @Test
    public void testMore() {
        int n = -9;
        System.out.println("-9的二进制：" + Integer.toBinaryString(n));
        n = -1;
        System.out.println("-1的二进制：" + Integer.toBinaryString(n));


        int max = Integer.MAX_VALUE;
        int min = Integer.MIN_VALUE;
        System.out.println("最大的整数： " + max);
        System.out.println("最小的整数:" + min);

        System.out.println("最大整数的二进制： " +
                Integer.toBinaryString(max));
        System.out.println("最小整数的二进制： " +
                Integer.toBinaryString(min));

   
    }

结果：

-9的二进制：11111111111111111111111111110111
-1的二进制：11111111111111111111111111111111
最大的整数： 2147483647
最小的整数:-2147483648
最大整数的二进制： 1111111111111111111111111111111
最小整数的二进制： 10000000000000000000000000000000

这里是32位，和我们探究的4位理论上是一样的。

那么，如何才能快速知道-9的二进制表示呢？

首先，你知道-1是32个1（11111111111111111111111111111111）

然后，因为-9是-1减掉8，所以你用32个1去减8（1000）

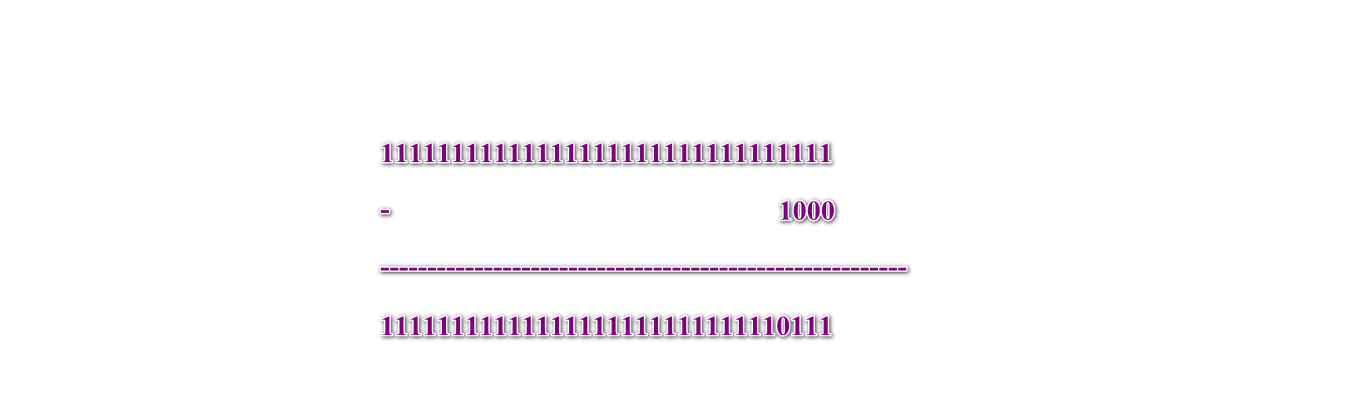
另外一个有趣的地方就是：

最大值加一变成最小值。

这个是正常现象，不能叫做溢出。

我们拿8位的byte做个例子：

    @Test
    public void testbyte() {
        byte b = 127;
        byte ans = (byte) (b + 1);
        System.out.println(ans);
    }

结果：

-128

溢出

还是看4位的情况。

1111如果还要加1，就会溢出。

溢出自动舍去高位：

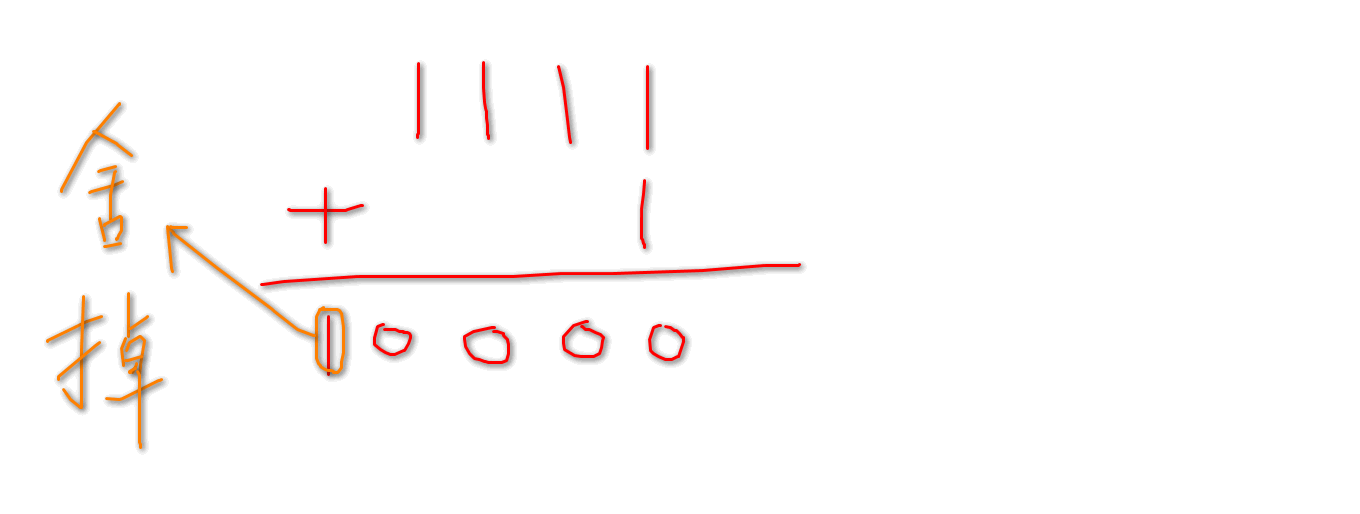
于是结果就是0000。

溢出保证我们的整个逻辑还是正确的。

数学移位

什么是数学移位？

就是>>以及<<。

它是二进制数的移动，所以计算起来非常之快。

当然，你完全可以将其理解为乘2和除2。

>>是右移，右移它的数量级就会降低，移一次就会有除以2的效果。

相反，<<是左移，左移一次就会有乘以2的效果。

看个测试：

  @Test
    public void testMoveBit(){
        System.out.println(50>>1);
        System.out.println(50<<1);
        System.out.println(50>>2);
        System.out.println(50<<2);
        System.out.println("------------------------");
        System.out.println(-50>>1);
        System.out.println(-50<<1);
        System.out.println(-50>>2);
        System.out.println(-50<<2);
    }

结果：

25
100
12
200
------------------------
-25
-100
-13
-200

唯一要注意的就是除不尽的时候要取整。

还有一个很经典的问题，就是右移的时候，高位到底是补0还是补1。

用代码看一下就知道了：

  @Test
    public void testMoveBitPositiveAndNegative(){
        System.out.println("positive--------------------");
        System.out.println(Integer.toBinaryString(50));
        System.out.println(Integer.toBinaryString((50>>2)));
        System.out.println("negative--------------------");
        System.out.println(Integer.toBinaryString((-50)));
        System.out.println(Integer.toBinaryString((-50>>2)));
    }

结果：

positive--------------------
110010
1100
negative--------------------
11111111111111111111111111001110
11111111111111111111111111110011

正50它把前面的0全部给省略了，我们自己补上：

正数数学右移的时候，就是高位补0，低位溢出。

负数数学右移的时候，从控制台的结果可以看到，是高位补1，低位溢出。

逻辑位移

逻辑位移只有右移，没有左移，右移的符号是>>>。

它的作用很大，源码中经常出现逻辑右移，主要作用就是用来将数字拆分成一个一个字节的。

    @Test
    public void testMoveBitLogic(){
        System.out.println(50>>>1);
        System.out.println(50>>>2);
        System.out.println("------------------------");
        System.out.println(-50>>>1);
        System.out.println(-50>>>2);
    }

结果：

25
12
------------------------
2147483623
1073741811

正数的行为和数学右移很像。但是，它不是用来做数学计算的。所以如果你想要快速地完成除以2的工作，请用>>。

负数的右移很奇怪，那就是高位补0还是补1的问题了。

测试：

    @Test
    public void testMoveBitLogicBinary(){
        System.out.println("positive--------------------");
        System.out.println(Integer.toBinaryString(50));
        System.out.println(Integer.toBinaryString((50>>>2)));
        System.out.println("negative--------------------");
        System.out.println(Integer.toBinaryString((-50)));
        System.out.println(Integer.toBinaryString((-50>>>2)));
    }

结果：

positive--------------------
110010
1100
negative--------------------
11111111111111111111111111001110
111111111111111111111111110011

正数的时候和数学右移一样，都是高位补0。

负数的时候，我们睁大眼睛看看：

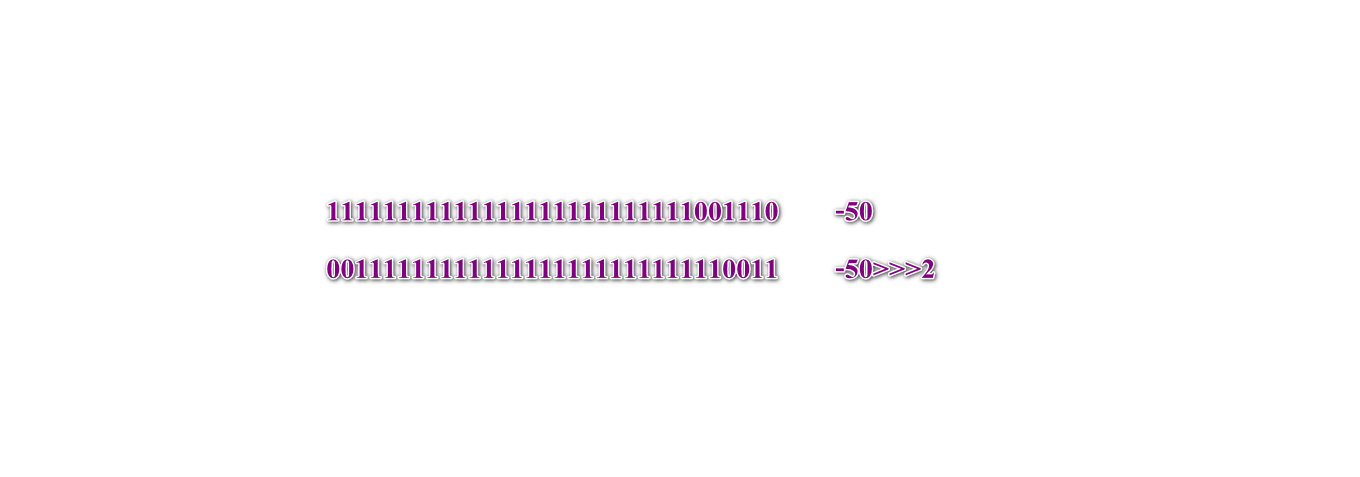
负数逻辑右移，是高位补0，低位溢出。

逻辑右移的应用

看一下RandomAccessFile的writeInt方法：

 public final void writeInt(int v) throws IOException {
        write((v >>> 24) & 0xFF);
        write((v >>> 16) & 0xFF);
        write((v >>>  8) & 0xFF);
        write((v >>>  0) & 0xFF);
        //written += 4;
    }

可以看出来，它是一个一个字节写出去的，从高八位开始。

其实在网络传输中，传输的都是字节，所以也会用到逻辑右移。

最后

以上就是内向墨镜为你收集整理的二进制基础：补码，左移，右移的全部内容，希望文章能够帮你解决二进制基础：补码，左移，右移所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。