补码的移位运算

75 阅读 0 评论 50 点赞

我是靠谱客的博主会撒娇小懒猪，最近开发中收集的这篇文章主要介绍补码的移位运算，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

通常情况下，计算机中的有符号数以补码形式存储。
补码的深入理解

对补码进行左移运算： 移出的位补0。
符号位也可能会发生改变，从而导致数的正负发生改变。
在没有发生符号位的改变时，左移一位相当于 $\times 2$ 。特别的，当数为负数时，该性质也成立：

假设计算机中的数以8bit存储：

补码	原码	数
0111 1000	0111 1000	120
1111 0000	1001 0000	-16
1110 0000	1010 0000	-32
1100 0000	1100 0000	-64
1000 0000	无法用原码表示	-128
0000 0000	0000 0000	0

左移的极限值为0.

对补码进行右移运算：

对正整数（符号位为0）进行右移：移出的位补0
对负整数（符号位为1）进行右移：移出的位补1，结果仍是负数

正整数右移的极限值为0，负整数右移的极限值为-1.

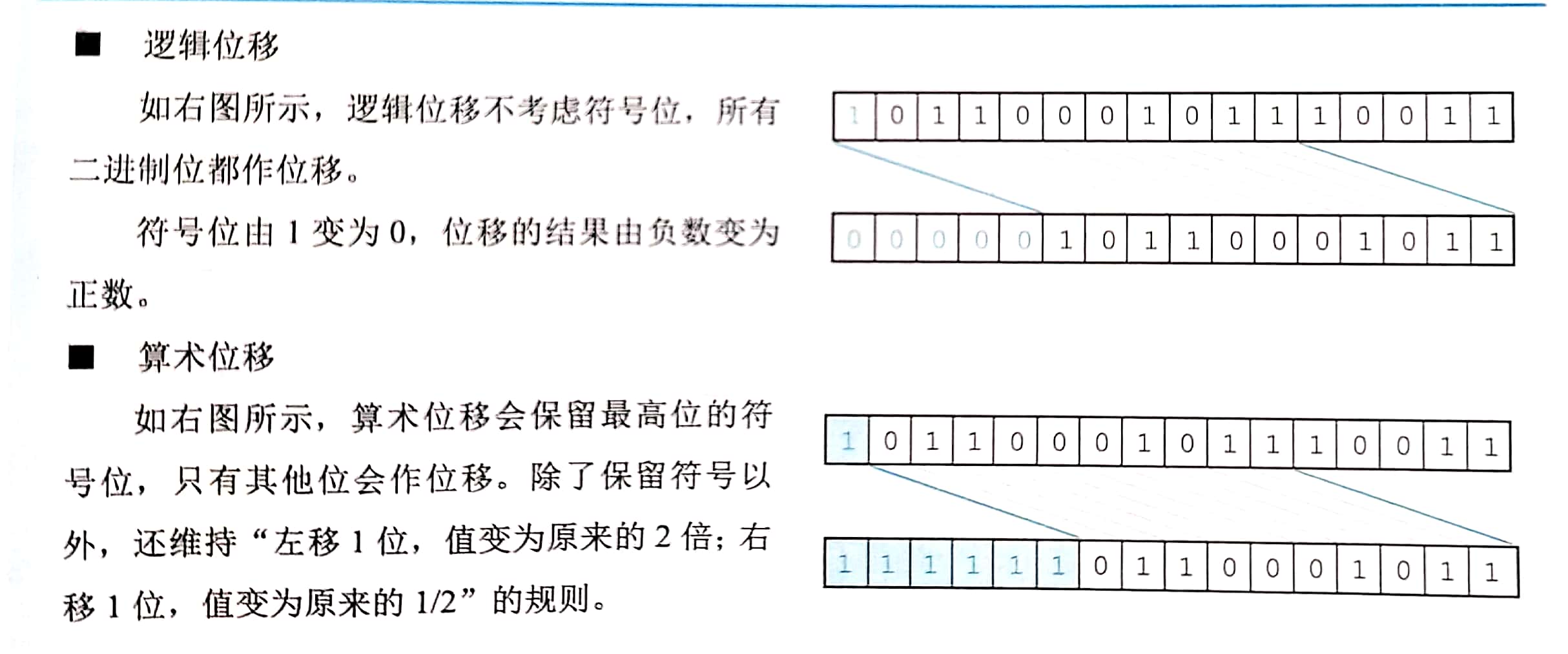
事实上，当为负数时，右移时最高位补0还是补1取决于编译系统的规定。（补0的称为“逻辑右移”，补1的称为“算术右移”。）因此，尽量不要对负数作位移！

注意：
无论是算术右移还是逻辑右移，操作后的结果都是原来的数除以2。对于无符号数，采用的是逻辑右移（补0）；对于有符号数，采用的是算术右移。算术右移时，左侧补原符号位的数字。