写在前面（2022年12月6日更新）：

感谢评论区@ZSTU_QWQ的指出，新版本的MATLABdesolve函数直接按旧版本的写法写会出现报警告或者错误。我用2021b版本的MATLAB采用原来的代码会出现下面的警告：

所以我更改了原文，附上了旧版本和新版本的两种写法，都经过验证，代码是可行的，有错误欢迎在评论区指出。

-----------------------------------------------以下是原文-----------------------------------------------

1.desolve函数

desolve函数用于求解微分方程或微分方程组，话不多说，直接上例子：

1.1 求dy/dt=5的微分方程

旧版本的MATLAB写法

y1=dsolve(‘Dy==5’)

新版本的MATLAB写法

syms y(t)
eqn = diff(y,t) == 5;
y1 = dsolve(eqn)

1.2 求dy/dx=x的微分方程，x为自变量

旧版本的MATLAB写法

y2=dsolve(‘Dy==x’,‘x’)

新版本的MATLAB写法

syms y(x)
eqn = diff(y,x) == x;
y2 = dsolve(eqn)

1.3 求d2y/dt2=1+dy/dt的微分方程

旧版本的MATLAB写法

y3=dsolve(‘D2y==1+Dy’)

新版本的MATLAB写法

syms y(t)
eqn = diff(y,t,2) == 1+diff(y,t);
y3= dsolve(eqn)

1.4 求d2y/dt2=1+dy/dt的微分方程，初始条件y(0)=1,dy(0)/dt=0

旧版本的MATLAB写法

y4=dsolve(‘D2y==1+Dy’,‘y(0)==1’,‘Dy(0)==0’)

新版本的MATLAB写法

syms y(t)
Dy = diff(y);
eqn = diff(y,t,2) == 1+diff(y,t);
cond1 = y(0) == 1;
cond2 = Dy(0) == 0;
conds = [cond1 cond2];
y4 = dsolve(eqn,conds)

1.5 dx/dt=y+x,dy/dt=2*x的微分方程组的解，x=y5,y=y6

旧版本的MATLAB写法

[y5,y6]=dsolve(‘Dx == y+x’,‘Dy==2*x’)

新版本的MATLAB写法

syms x(t) y(t)
eqn1 = diff(x,t) == y+x;
eqn2 = diff(y,t) == 2*x;
eqn=[eqn1,eqn2];
[y5,y6]=dsolve(eqn)

1.6 dx/dt=y+x,dy/dt=2*x的微分方程组的解，初始条件x(0)=0,y(0)=1,x=y5,y=y6

旧版本的MATLAB写法

[y7,y8] = dsolve(‘Dx == y+x’,‘Dy==2*x’,‘x(0)==0’,‘y(0)==1’)

新版本的MATLAB写法

syms x(t) y(t)
eqn1 = diff(x,t) == y+x;
eqn2 = diff(y,t) == 2*x;
cond1 = x(0) == 0;
cond2 = y(0) == 1;
eqn = [eqn1,eqn2];
cond = [cond1,cond2];
[y7,y8] = dsolve(eqn,cond)

1.7 求dy/dx=-2y+2x^2+2*x,初始条件y(0)==1，x为自变量

旧版本的MATLAB写法

y9=dsolve(‘Dy==-2y+2x^2+2*x’,‘y(0)==1’,‘x’)

新版本的MATLAB写法

syms y(x)
eqn = diff(y,x) == -2*y+2*x^2+2*x;
cond = y(0) == 1;
y9 = dsolve(eqn,cond)

注意：旧版本的MATLAB里dsolve函数用单引号将方程引起来，方程里不能用.*或者.^ 的符号。新版本用syms进行代替没有这个要求。

2.solve函数

solve函数用于求解一般的方程（非微分方程），话不多说，直接上例子：

2.1 求sin(x)=1/2方程的根

x1=solve(sin(x)==1/2)

2.2 求x^3-1==0方程的根

x2=solve(x.^3-1==0)

2.3 求ax+b=0的解

syms f x a b 
f=a*x+b;
x3=solve(f,x) %x3=-b/a

2.4 求二元一次方程组x+y=1和2x-y=1的解

syms x y 
s=solve(x+y-1,2*x-y-1,x,y);%s是一个结构体
s.x % x=2/3
s.y % y=1/3

2.5 求解二阶微分方程（方程如下）

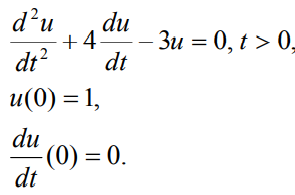
syms r 
l=solve(r^2+4*r-3,r) 
syms t c1 c2 
u=c1*exp(l(1)*t)+c2*exp(l(2)*t)
c=solve(subs(u,t,sym(0))-1,subs(diff(u,t),t,sym(0)),c1,c2)
u=subs(u,{c1,c2},{c.c1,c.c2}) 
tt=linspace(0,5,21); 
plot(tt,subs(u,t,tt)) 

结果：

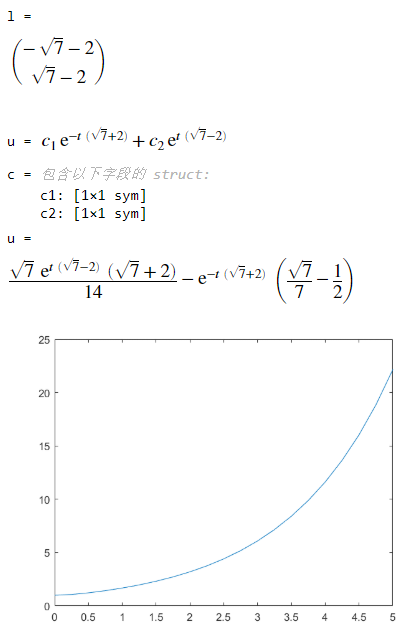
注意：solve函数不用单引号将方程引起来，方程里可以用.*或者.^ 的符号，也可以不用。

最后

以上就是温婉牛排为你收集整理的matlab中desolve、solve函数的应用1.desolve函数2.solve函数的全部内容，希望文章能够帮你解决matlab中desolve、solve函数的应用1.desolve函数2.solve函数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。