数论 | 容斥定理

65 阅读 0 评论 43 点赞

我是靠谱客的博主留胡子铃铛，最近开发中收集的这篇文章主要介绍数论 | 容斥定理，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

#容斥定理

######参考文章：容斥定理详解
###摘要：
######原理描述：
计算几个集合并集的大小，先计算出所有单个集合的大小，减去所有两个集合相交的部分，加上三个集合相交的部分，再减去四个集合相交的部分，以此类推，一直计算到所有集合相交的部分。具体如图：
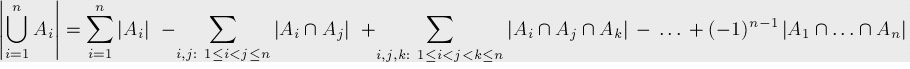
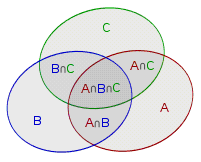
这里写图片描述
######维恩图：

######概率论:
事件Ai(i=1,…,n)，P(Ai)为对应事件发生的概率。至少一个事件发生的概率：

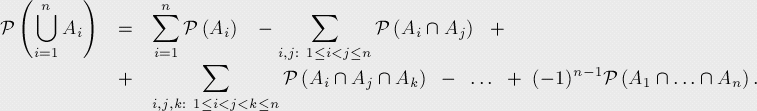
######方法论：
容斥常用二进制的方法进行枚举，第k位为1则表示选择了第k个数，用bits统计奇偶来确定符号，具体如下：

for(int i=1;i<(1<<k);++i)
    {
        bits=0;
        for(int j=0;j<k;++j)
        {
            if((1<<j)&i)
            {
                /**视具体情况填写**/
                ++bits;
            }
        }
        t=/** 计算交集的值 **/;
        if(bits&1) ans+=t;
        else ans-=t;
    }

##例题

###codeforce gym 101350G. Snake Rana
######题意：
在一个nm的矩形里，有k个方格放置了炸弹，询问不包含炸弹的矩形有多少个？
######数据范围：
$1 ≤ N, M ≤ {10^4}, 1 ≤ K ≤ 20$
######题解：
nm的矩形中，共有 $n ∗ ( n + 1 ) 2 frac{n*(n+1)}2$ * $m ∗ ( m + 1 ) 2 frac{m*(m+1)}2$ 个矩形。(详见:矩形A+B)然后用位运算枚举包含炸弹的情况，用所有的情况减去包含炸弹的情况就是最终结果。
######代码:

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#define LL long long

using namespace std;

const int maxn=1e4+10;
int x[maxn],y[maxn];
int n,m,k;

LL f()
{
    LL ans=0,t;
    int x1,x2,y1,y2;
    int bits=0;
    for(int i=1;i<(1<<k);++i)
    {
        bits=0;
        for(int j=0;j<k;++j)
        {
            if((1<<j)&i)
            {
                if(!bits) x1=x2=x[j],y1=y2=y[j];
                else
                {
                    x1=min(x1,x[j]);
                    y1=min(y1,y[j]);
                    x2=max(x2,x[j]);
                    y2=max(y2,y[j]);
                }
                ++bits;
            }
        }
        t=x1*1ll*(n-x2+1)*y1*(m-y2+1);
        if(bits&1) ans+=t;
        else ans-=t;
    }
    return ans;
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d%d",&n,&m,&k);
        for(int i=0;i<k;++i)
            scanf("%d%d",&x[i],&y[i]);
        LL ans=(m+1)*1ll*m*(n+1)*n/4;
        ans=ans-f();
        printf("%lldn",ans);
    }
    return 0;
}

###[HDU4135 - Co-prime](http://acm.hdu.edu.cn/showproblem.php?pid=4135) ######题意：给定A,B,n，询问区间[A,B]中与n互质的数有多少个？ ######数据范围： $1 <= A <= B <= {10^15}, 1 <=N <= {10^9}$ ######题解： A,B的数据范围太大，枚举显然不显示。互质就是指最大公约数为1，那么不互质就是有相同的大于1的公约数。把n进行因数分解，因数的倍数就是不互质的，用所有的方案数$-$不互质的就是结果，注意这里要进行容斥，因为会有类似于“2的倍数同样也是4的倍数，也是8的倍数...”这样的情况出现。 ######代码：

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#define LL long long

using namespace std;

const int maxn=1e5+10;
int a[maxn];

int main()
{
    int T,c=1;
    scanf("%d",&T);
    LL L,R;
    int n;
    while(T--)
    {
        scanf("%lld%lld%d",&L,&R,&n);
        --L;

        int cnt=0;
        for(int i=2;i*i<=n;++i)
        {
            if(n%i==0)
            {
                a[cnt++]=i;
                while(n%i==0)
                {
                    n=n/i;
                }
            }
        }
        if(n>1) a[cnt++]=n;

        LL ans1=0,ans2=0,d;
        int bits;
        for(int i=1;i<(1<<cnt);++i)
        {
            d=1;
            bits=0;
            for(int j=0;j<cnt;++j)
            {
                if((1<<j)&i)
                {
                    d=d*1ll*a[j];
                    bits++;
                }
            }
            if(bits&1) ans1+=L/d,ans2+=R/d;
            else ans1-=L/d,ans2-=R/d;
        }
        LL ans=R-L-(ans2-ans1);
        printf("Case #%d: %lldn",c++,ans);
    }

    return 0;
}