数据结构–图(Graph)详解(一)

一、图的基本概念

我们知道，数据之间的关系有 3 种，分别是 “一对一”、“一对多” 和 “多对多”，前两种关系的数据可分别用线性表和树结构存储，接下来学习存储具有"多对多"逻辑关系数据的结构——图存储结构。

1.图的分类

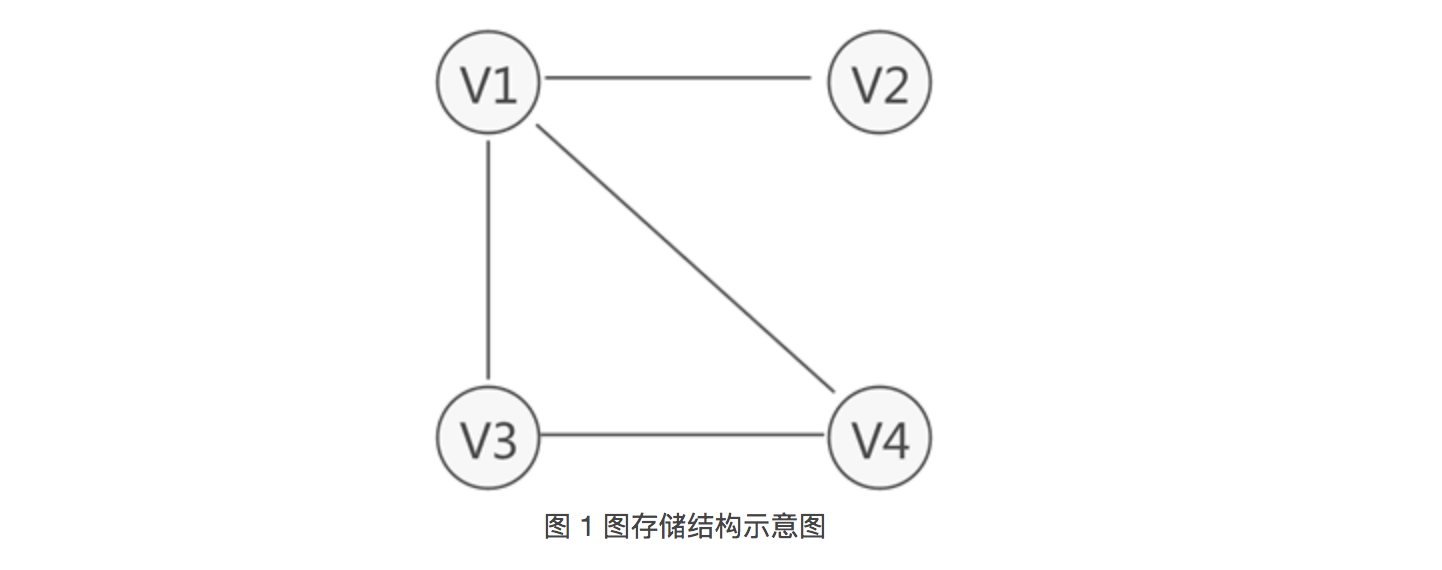
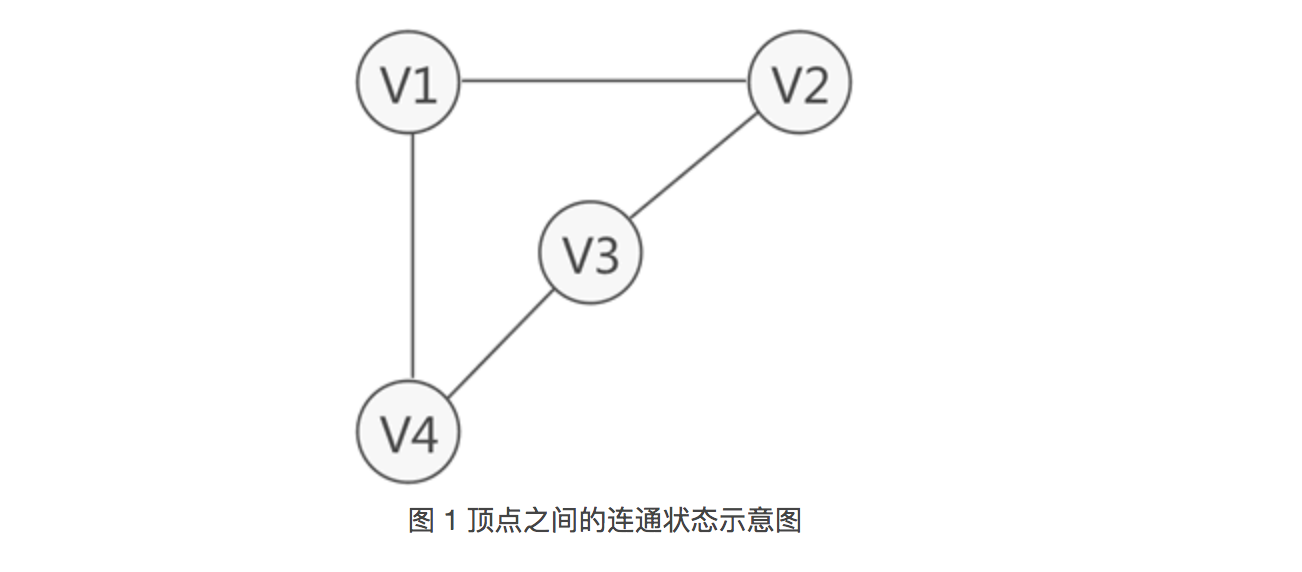
图 1 所示为存储 V1、V2、V3、V4 的图结构，从图中可以清楚的看出数据之间具有的"多对多"关系。例如，V1 与 V4 和 V2 建立着联系，V4 与 V1 和 V3 建立着联系，以此类推。

与链表不同，图中存储的各个数据元素被称为顶点（而不是节点）。拿图 1 来说，该图中含有 4 个顶点，分别为顶点 V1、V2、V3 和 V4。
图存储结构中，习惯上用 Vi 表示图中的顶点，且所有顶点构成的集合通常用 V 表示，如图 1 中顶点的集合为 V={V1,V2,V3,V4}。

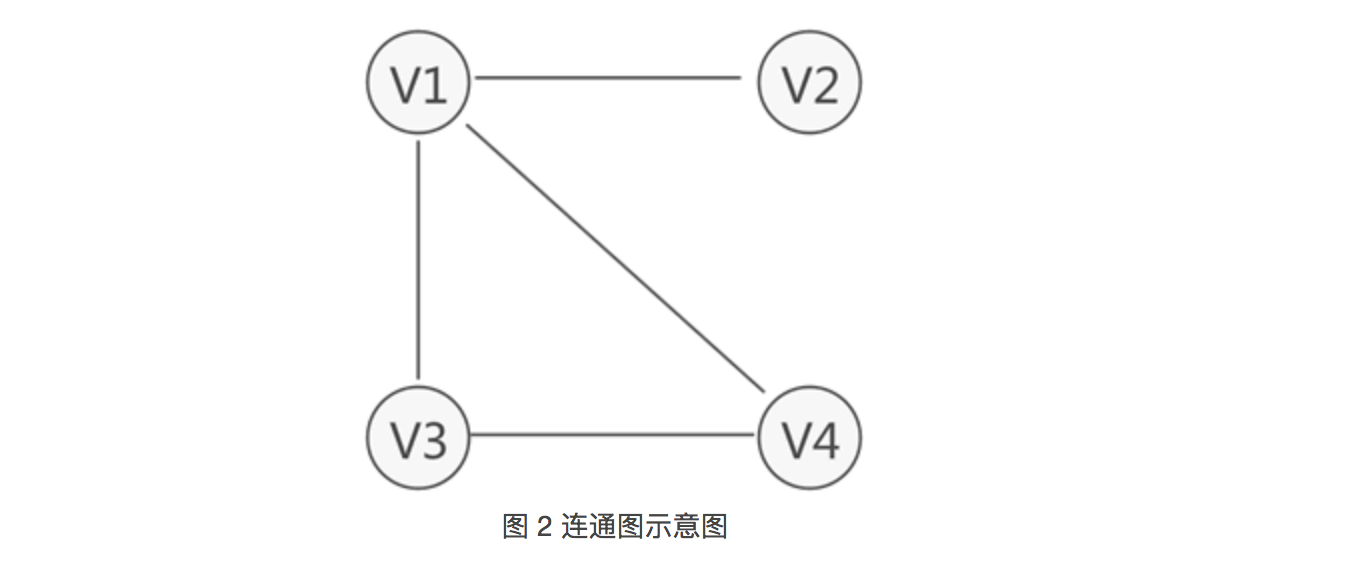
注意，图 1 中的图仅是图存储结构的其中一种，数据之间 “多对多” 的关系还可能用如图 2 所示的图结构表示：

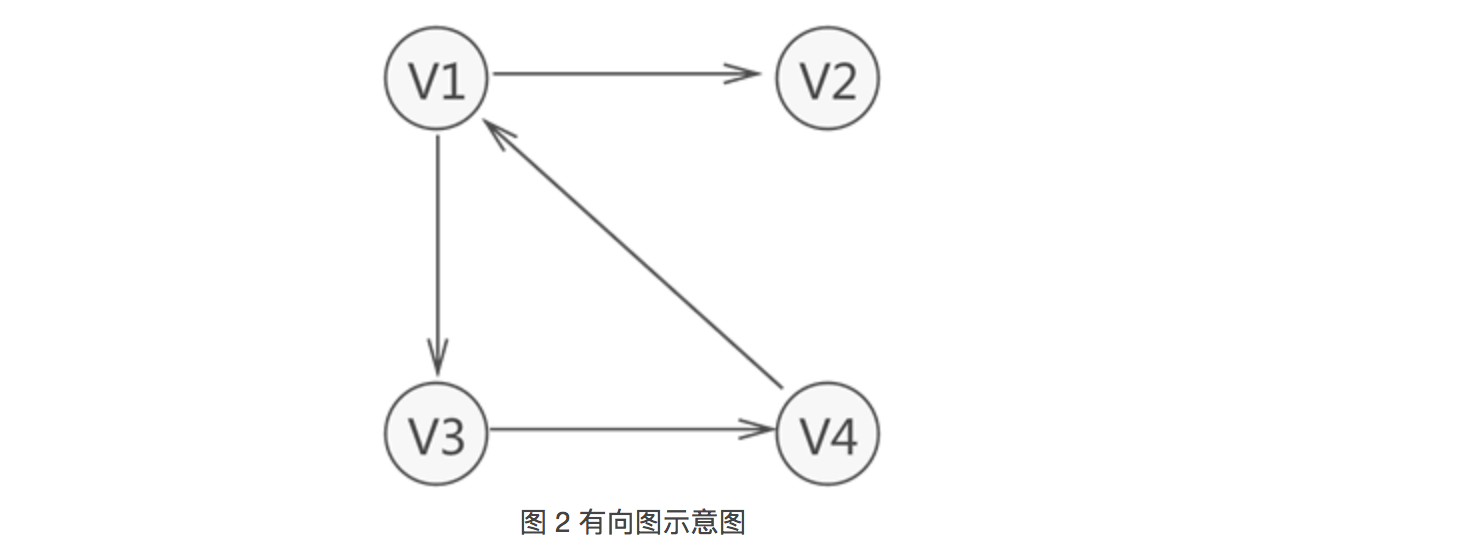
可以看到，各个顶点之间的关系并不是"双向"的。比如，V4 只与 V1 存在联系（从 V4 可直接找到 V1），而与 V3 没有直接联系；同样，V3 只与 V4 存在联系（从 V3 可直接找到 V4），而与 V1 没有直接联系，以此类推。

因此，图存储结构可细分两种表现类型，分别为无向图（图 1）和有向图（图 2）。

2.弧头和弧尾

有向图中，无箭头一端的顶点通常被称为"初始点"或"弧尾"，箭头直线的顶点被称为"终端点"或"弧头"。

3.入度和出度

• 对于有向图中的一个顶点 V 来说，箭头指向 V 的弧的数量为 V 的入度（InDegree，记为 ID(V)）；
• 箭头远离 V 的弧的数量为 V 的出度（OutDegree，记为OD(V)）

拿图 2 中的顶点 V1来说，该顶点的入度为 1，出度为 2（该顶点的度为 3）。

4.(V1,V2) 和 < V1,V2 > 的区别

• 无向图中描述两顶点（V1 和 V2）之间的关系可以用 (V1,V2) 来表示，而有向图中描述从 V1 到 V2 的"单向"关系用<V1,V2> 来表示。
• 由于图存储结构中顶点之间的关系是用线来表示的，因此 (V1,V2) 还可以用来表示无向图中连接 V1 和 V2 的线，又称为边；
• 同样，<V1,V2> 也可用来表示有向图中从 V1 到 V2 带方向的线，又称为弧。

5.集合 VR 的含义

• 并且，图中习惯用 VR 表示图中所有顶点之间关系的集合。
  例如，图 1 中无向图的集合 VR={(v1,v2),(v1,v4),(v1,v3),(v3,v4)}，图 2 中有向图的集合 VR={<v1,v2>,<v1,v3>,<v3,v4>,<v4,v1>}。

6.路径和回路

• 无论是无向图还是有向图，从一个顶点到另一顶点途径的所有顶点组成的序列（包含这两个顶点），称为一条路径。
• 如果路径中第一个顶点和最后一个顶点相同，则此路径称为"回路"（或"环"）。
• 并且，若路径中各顶点都不重复，此路径又被称为"简单路径"；
• 同样，若回路中的顶点互不重复，此回路被称为"简单回路"（或简单环）。

拿图 1 来说，从 V1 存在一条路径还可以回到 V1，此路径为 {V1,V3,V4,V1}，这是一个回路（环），而且还是一个简单回路（简单环）。

• 在有向图中，每条路径或回路都是有方向的。

7.权和网的含义

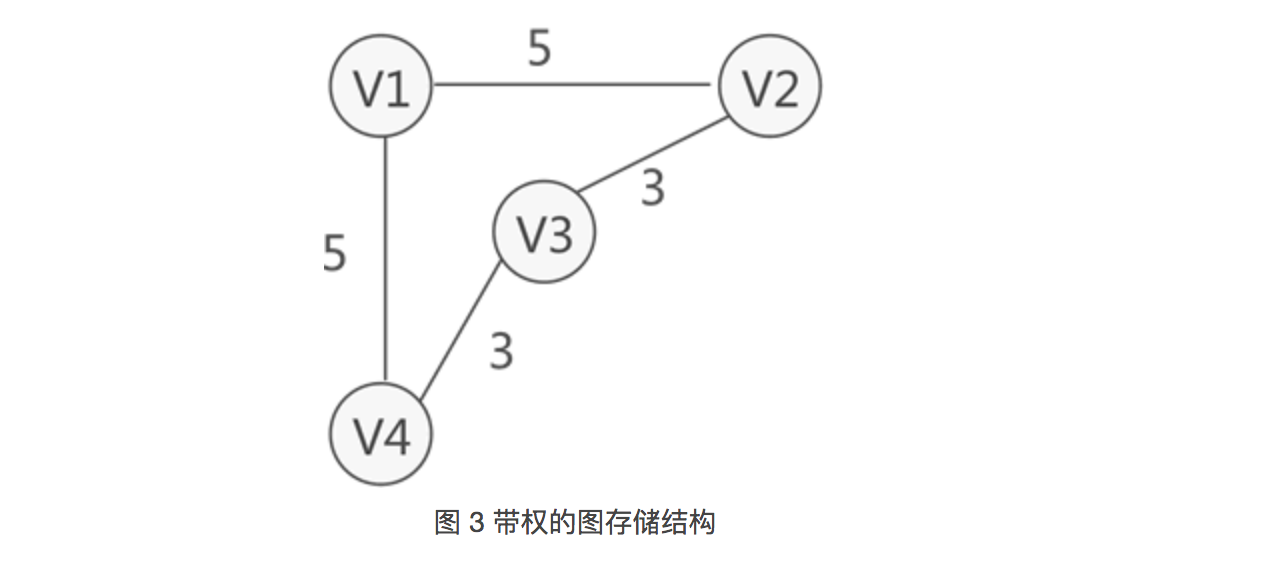
• 在某些实际场景中，图中的每条边（或弧）会赋予一个实数来表示一定的含义，这种与边（或弧）相匹配的实数被称为"权"，而带权的图通常称为网。

如图 3 所示，就是一个网结构：

8.子图

• 指的是由图中一部分顶点和边构成的图，称为原图的子图。

根据不同的特征，图又可分为完全图，连通图、稀疏图和稠密图：

9.完全图

• 若图中各个顶点都与除自身外的其他顶点有关系，这样的无向图称为完全图（如图 4a)）。
• 同时，满足此条件的有向图则称为有向完全图（图 4b)）。

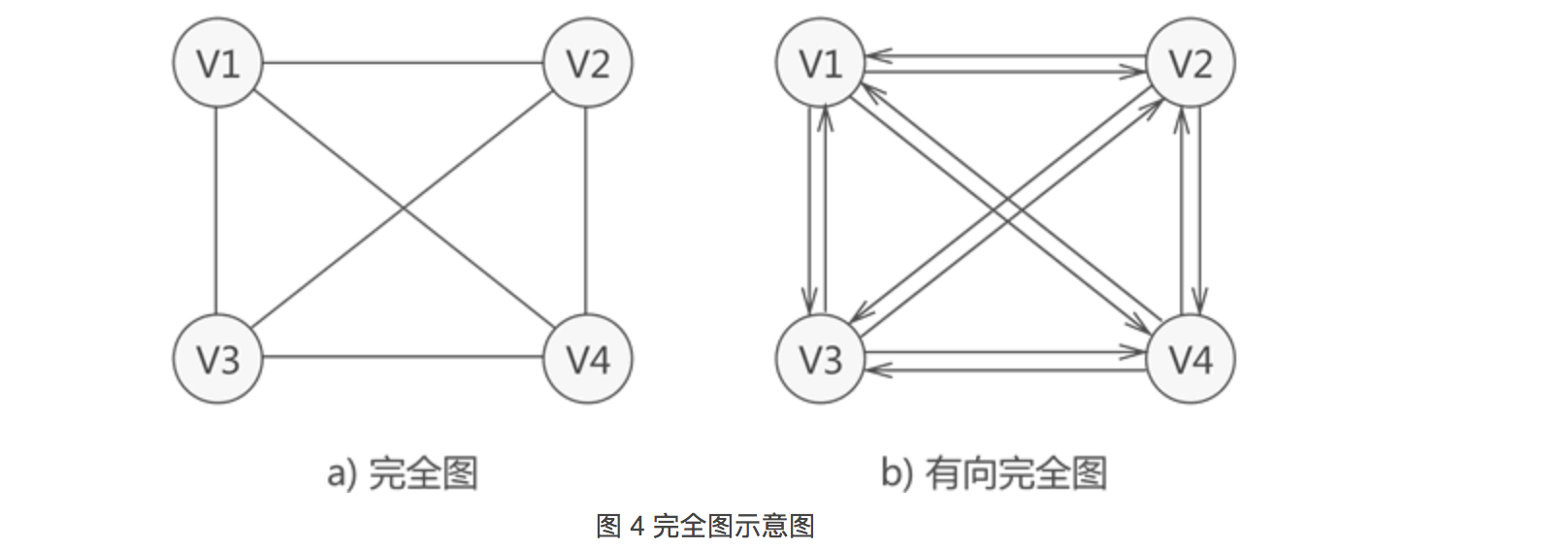
具有 n 个顶点的完全图，图中边的数量为 n(n-1)/2；而对于具有 n 个顶点的有向完全图，图中弧的数量为 n(n-1)。

10.稀疏图和稠密图

• 这两种图是相对存在的，即如果图中具有很少的边（或弧），此图就称为"稀疏图"；反之，则称此图为"稠密图"。

稀疏和稠密的判断条件是：e < nlogn，其中 e 表示图中边（或弧）的数量，n 表示图中顶点的数量。如果式子成立，则为稀疏图；反之为稠密图。

11.连通图

• 前面讲过，图中从一个顶点到达另一顶点，若存在至少一条路径，则称这两个顶点是连通着的。

例如图 1 中，虽然 V1 和 V3 没有直接关联，但从 V1 到 V3 存在两条路径，分别是 V1-V2-V3 和 V1-V4-V3，因此称 V1 和 V3 之间是连通的。

• 无向图中，如果任意两个顶点之间都能够连通，则称此无向图为连通图。

例如，图 2 中的无向图就是一个连通图，因为此图中任意两顶点之间都是连通的。

• 若无向图不是连通图，但图中存储某个子图符合连通图的性质，则称该子图为连通分量。
• 前面讲过，由图中部分顶点和边构成的图为该图的一个子图，但这里的子图指的是图中"最大"的连通子图（也称"极大连通子图"）。

如图 3 所示，虽然图 3a) 中的无向图不是连通图，但可以将其分解为 3 个"最大子图"（图 3b)），它们都满足连通图的性质，因此都是连通分量。

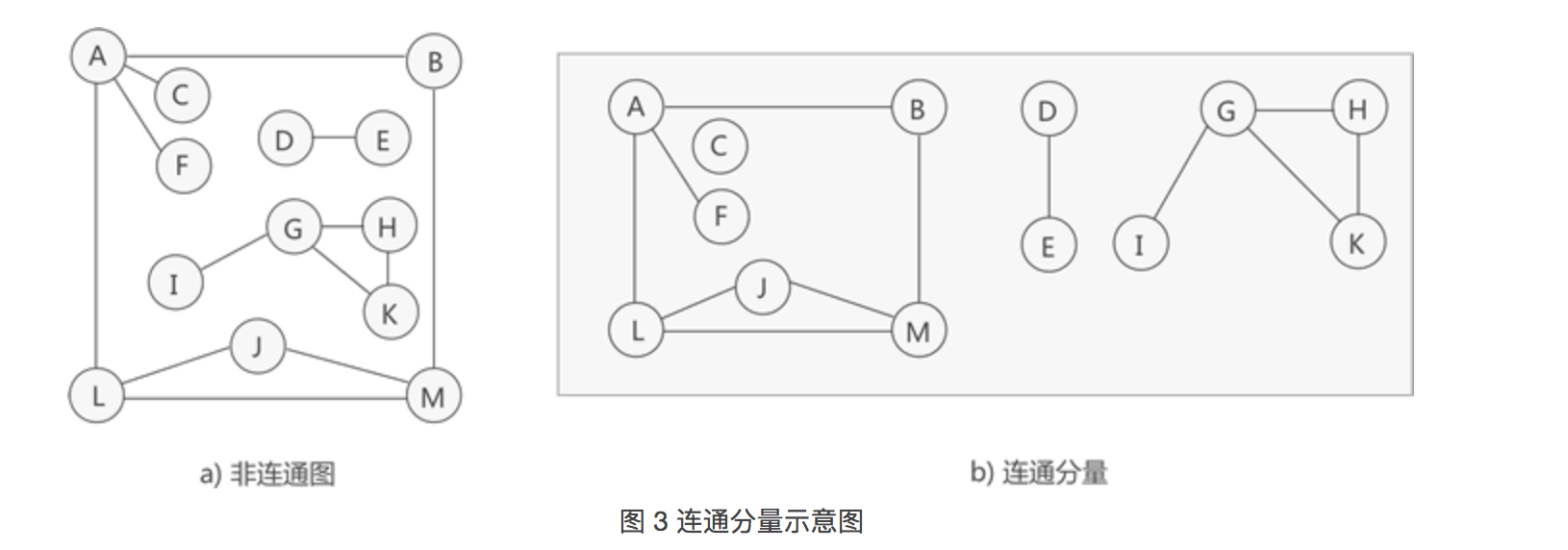
提示，图 3a) 中的无向图只能分解为 3 部分各自连通的"最大子图"。

需要注意的是，连通分量的提出是以"整个无向图不是连通图"为前提的，因为如果无向图是连通图，则其无法分解出多个最大连通子图，因为图中所有的顶点之间都是连通的。

12.强连通图

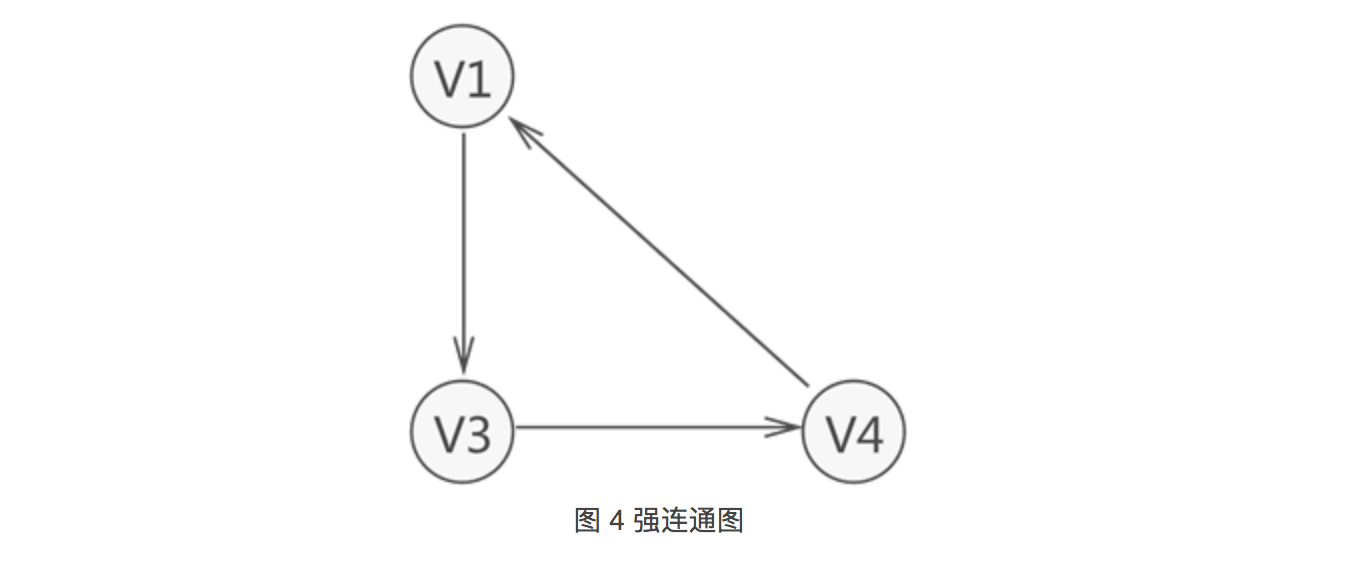
• 有向图中，若任意两个顶点 Vi 和 Vj，满足从 Vi 到 Vj 以及从 Vj 到 Vi都连通，也就是都含有至少一条通路，则称此有向图为强连通图。

如图 4 所示就是一个强连通图。

• 与此同时，若有向图本身不是强连通图，但其包含的最大连通子图具有强连通图的性质，则称该子图为强连通分量。
  
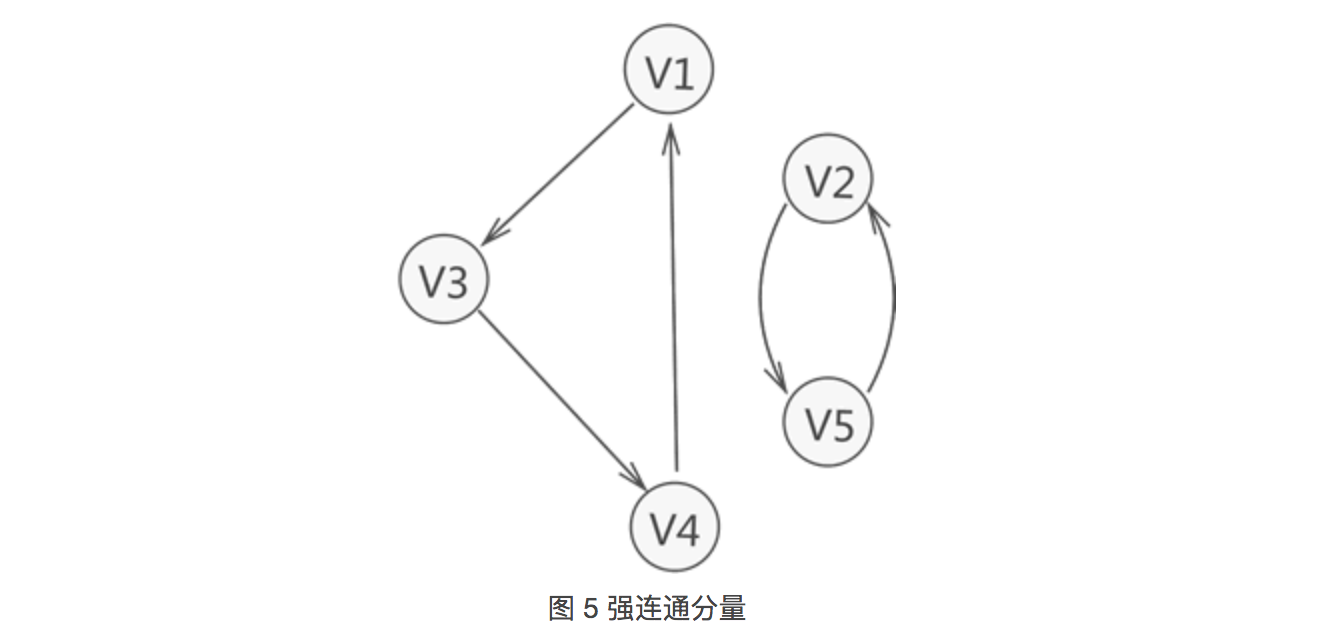
  如图 5 所示，整个有向图虽不是强连通图，但其含有两个强连通分量。

13.生成树

对连通图进行遍历，过程中所经过的边和顶点的组合可看做是一棵普通树，通常称为生成树。

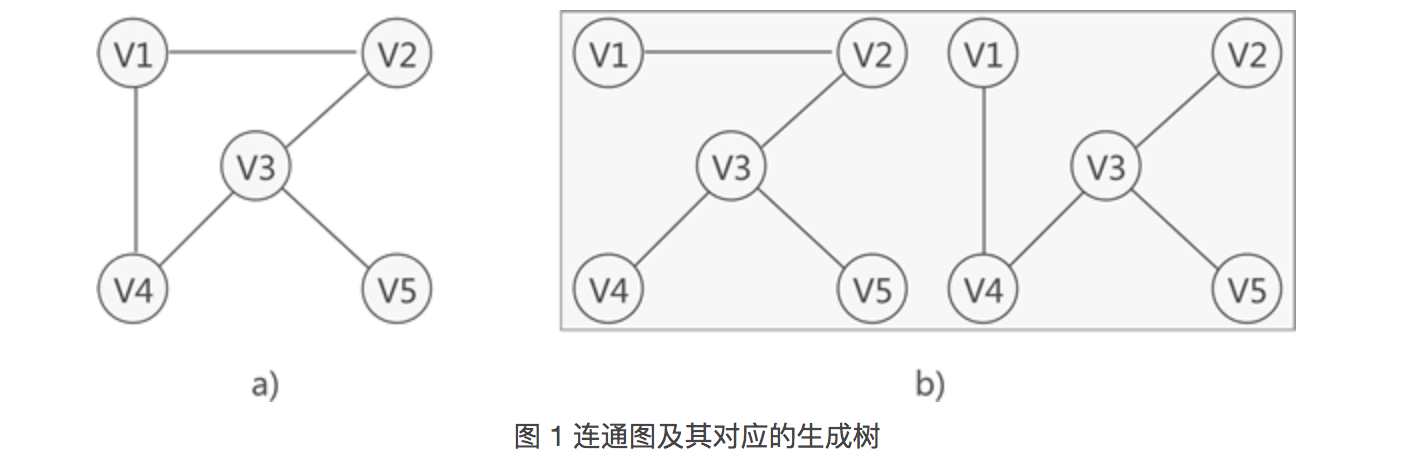
如图 1 所示，图 1a) 是一张连通图，图 1b) 是其对应的 2 种生成树。

连通图中，由于任意两顶点之间可能含有多条通路，遍历连通图的方式有多种，往往一张连通图可能有多种不同的生成树与之对应。

• 连通图中的生成树必须满足以下 2 个条件：
• 包含连通图中所有的顶点；
• 任意两顶点之间有且仅有一条通路；

因此，连通图的生成树具有这样的特征，即生成树中边的数量 = 顶点数 - 1。

14.生成森林

生成树是对应连通图来说，而生成森林是对应非连通图来说的。

我们知道，非连通图可分解为多个连通分量，而每个连通分量又各自对应多个生成树（至少是 1 棵），因此与整个非连通图相对应的，是由多棵生成树组成的生成森林。

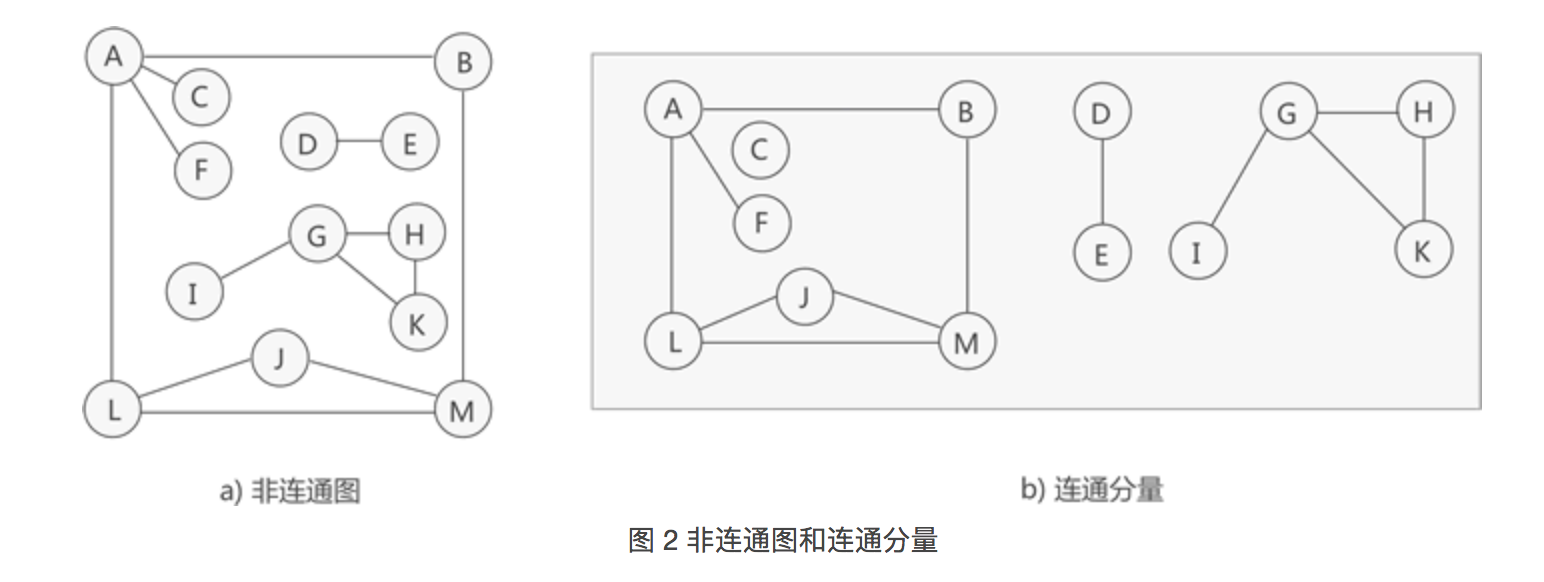
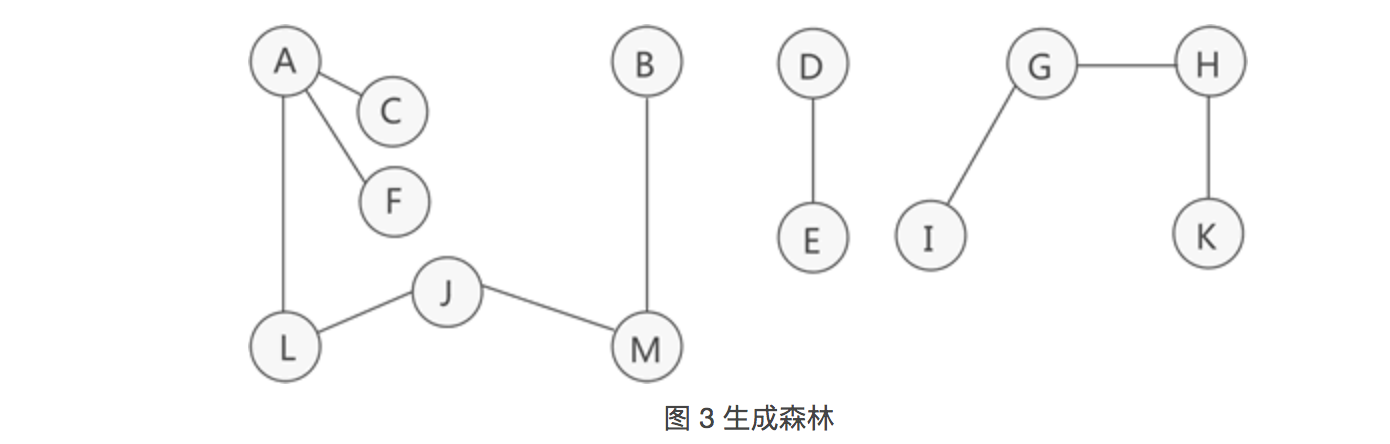
如图 2 所示，这是一张非连通图，可分解为 3 个连通分量，其中各个连通分量对应的生成树如图 3 所示：

15.重连通图及重连通分量

• 在无向图中，如果任意两个顶点之间含有不止一条通路，这个图就被称为重连通图。
• 在重连通图中，在删除某个顶点及该顶点相关的边后，图中各顶点之间的连通性也不会被破坏。
• 在一个无向图中，如果删除某个顶点及其相关联的边后，原来的图被分割为两个及以上的连通分量，则称该顶点为无向图中的一个关节点（或者“割点”）。

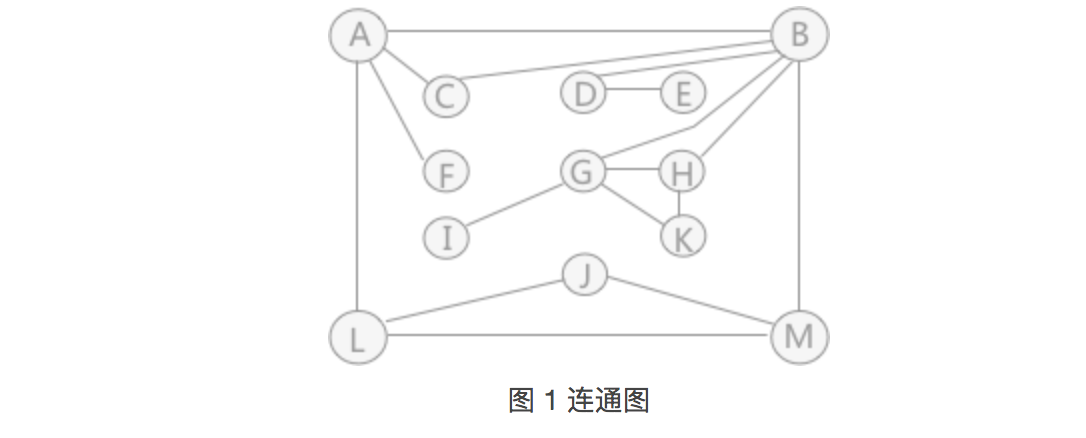
图 1 是连通图但不是重连通图，图中有4个关节点，分别是：A、B、D 和 G。比如删除顶点 B 及相关联的边后，原图就变为：

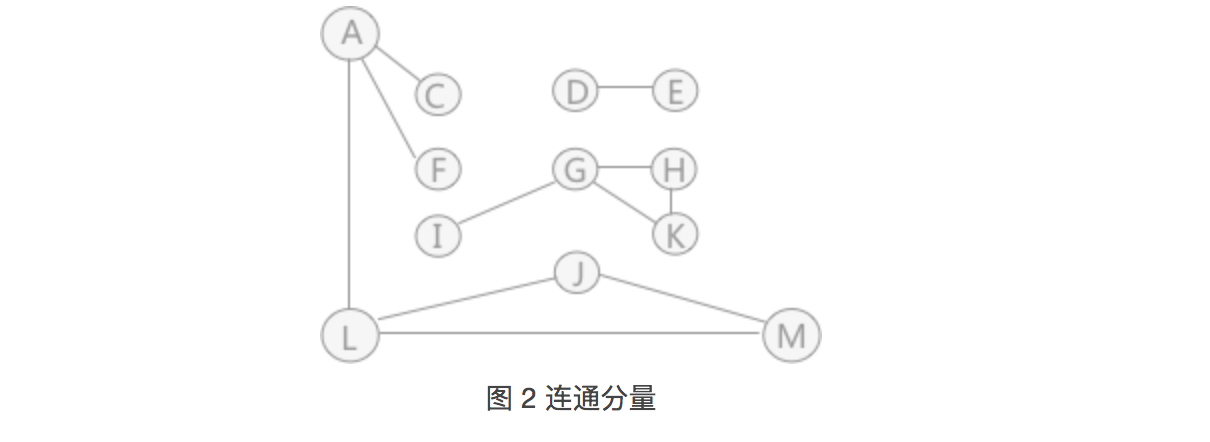
可以看到，图被分割为各自独立的 3 部分，顶点集合分别为：{A、C、F、L、M、J}、{G、H、I、K} 和 {D、E}。

• 了解了什么是关节点后，重连通图其实就是没有关节点的连通图。

• 在重连通图中，只删除一个顶点及其相关联的边，肯定不会破坏其连通性。

• 如果一味地做删除顶点的操作，直到删除 K 个顶点及其关联的边后，图的连通性才遭到破坏，则称此重连通图的连通度为 K 。

• 重连通图的实际应用

如今的通信网络对人们的生活有着重要的影响，如果将通信网络比做一个巨大的连通图的话，它的连通度 K
值越高，证明其稳定性越好，即使某一个站点发生故障无法工作也不会影响整个系统的正常工作。

同样，小到城市之间，大到国家之间的航空网也可以看作是一个连通图，但如果此图建设成为重连通图，当某条航线因为天气等因素关闭时，飞机仍可以从别的航线到达目的地。

在战争中，有“兵马未动，粮草先行”的说法，可见后勤补给对军队的重要性。如果补给线是一个重连通图，就不用过于担心补给线被破坏的问题，因为即使破坏一条，还有其它的，只要连通度足够大。
判断重连通图的方法

了解了什么是重连通图之后，如何编写程序直接判断一个图是否是重连通图呢？

对于任意一个连通图来说，都可以通过深度优先搜索算法获得一棵深度优先生成树，例如，图 1 通过深度优先搜索获得的深度优先生成树为：

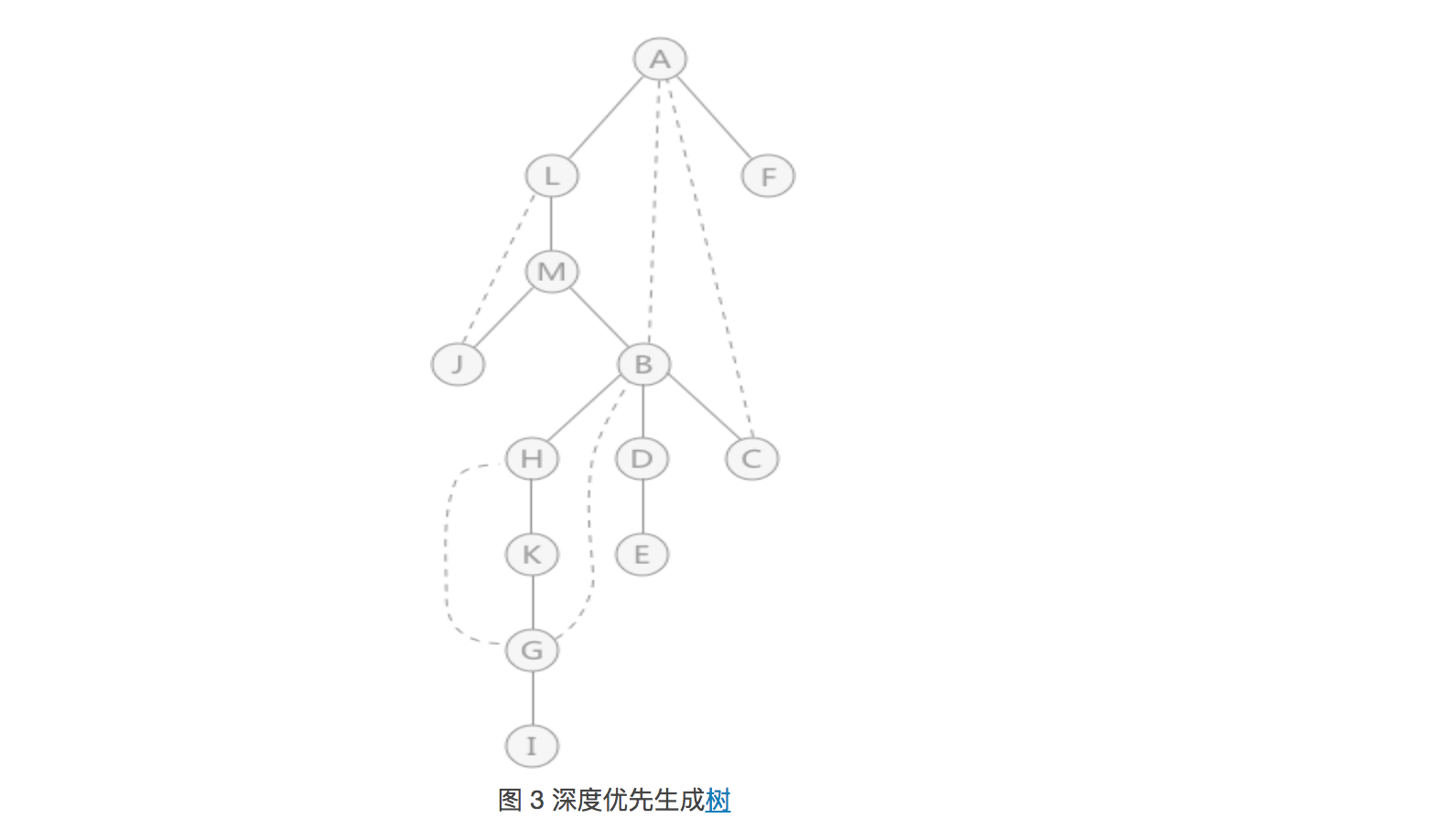
虚线表示遍历生成树时未用到的边，简称“回边”。也就是图中有，但是遍历时没有用到，生成树中用虚线表示出来。

• 在深度优先生成树中，图中的关节点有两种特性：
• 首先判断整棵树的树根结点，如果树根有两条或者两条以上的子树，则该顶点肯定是关节点。因为一旦树根丢失，生成树就会变成森林。
• 然后判断生成树中的每个非叶子结点，以该结点为根结点的每棵子树中如果有结点的回边与此非叶子结点的祖宗结点相关联，那么此非叶子结点就不是关节点；反之，就是关节点。

注意：必须是和该非叶子结点的祖宗结点（不包括结点本身）相关联，才说明此结点不是关节点。

• 所以，判断一个图是否是重连通图，也可以转变为：判断图中是否有关节点，如果没有关节点，证明此图为重连通图；反之则不是。
• 拿图 3 的生成树来说，利用两个特性判断每个顶点是否为关节点：
• 首先，判断树根结点 A ，由于有两个孩子，也就是有两棵子树，所以 A 是关节点。
• 然后判断树中所有的非叶子结点，也就是： L 、 M 、 B 、 D 、 H 、 K 、 G ；
• L 结点为根结点的子树中 B 结点有回边直接关联 A ，所以， L 不是关节点；
• 在以 M 结点为树根的子树中，J 结点和 B 结点都有回边关联 M 结点的祖宗结点，所以，M 不是关节点；
• 以 B 结点为根结点的 3 棵子树中，只有一棵子树（只包含结点 C ）与 B 结点的祖宗结点 A 有关联，其他两棵子树没有，所以结点 B 是关节点；
• 以 D 结点为根结点的子树中只有结点 E，且没有回边与祖宗结点关联，所以，D 是关节点；
• 以 H 结点为根结点的子树中， G 结点与 B 结点关联，所以， H 结点不是关节点；
• K 结点和 H 结点相同，由于 G 结点与祖宗结点 B 关联，所以 K 结点不是关节点；
• 以 G 结点为根结点的子树中只有一个结点 I，没有回边，所以结点 G 是关节点；

综上所述，图 3 中的关节点有 4 个，分别是： A 、 B 、 D 、 G 。

16.AOE网

AOE 网是在 AOV 网的基础上，其中每一个边都具有各自的权值，是一个有向无环网。其中权值表示活动持续的时间。

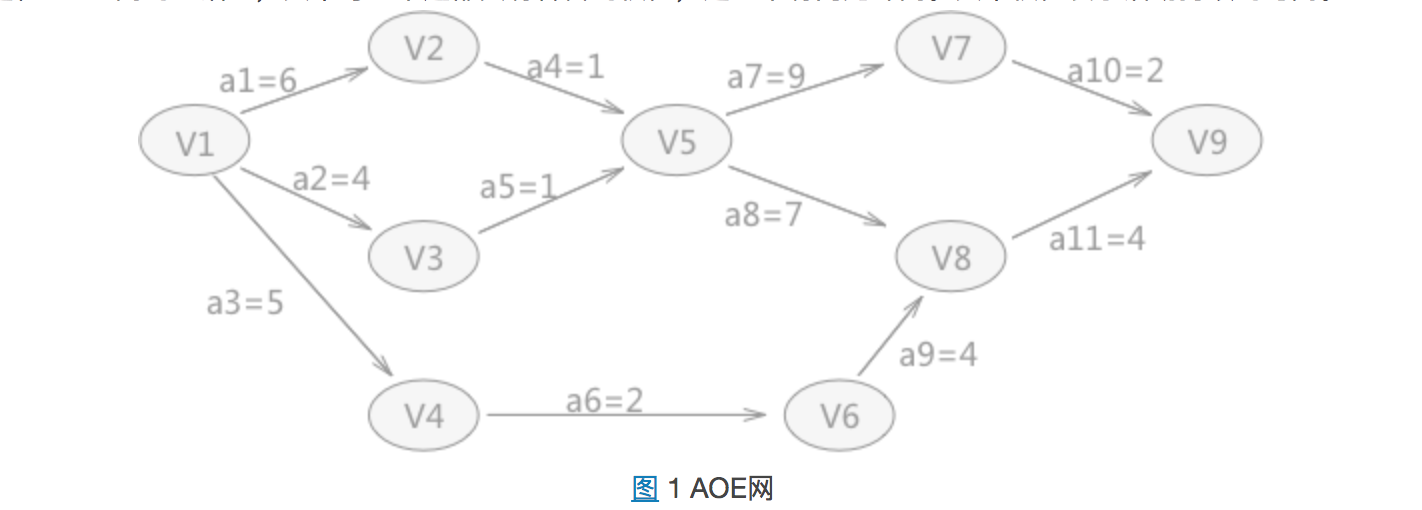
如图 1 所示就是一个 AOE 网，例如 a1=6 表示完成 a1 活动完成需要 6 天；

AOE 网中每个顶点表示在它之前的活动已经完成，可以开始后边的活动，

例如 V5 表示 a4 和 a5 活动已经完成，a7 和 a8 可以开始。

使用 AOE 网可以帮助解决这样的问题：如果将 AOE 网看做整个项目，那么完成整个项目至少需要多少时间？

解决这个问题的关键在于从 AOE 网中找到一条从起始点到结束点长度最长的路径，这样就能保证所有的活动在结束之前都能完成。

起始点是入度为 0 的点，称为“源点”；结束点是出度为 0 的点，称为“汇点”。这条最长的路径，被称为”关键路径“。

17.关键路径

• 为了求出一个给定 AOE 网的关键路径，需要知道以下 4 个统计数据：
• 对于 AOE 网中的顶点有两个时间：最早发生时间（用 Ve(j) 表示）和最晚发生时间（用 Vl(j) 表示）；
• 对于边来说，也有两个时间：最早开始时间（用 e(i) 表示）和最晚开始时间（ l(i) 表示）。
• Ve(j)： 对于 AOE 网中的任意一个顶点来说，从源点到该点的最长路径代表着该顶点的最早发生时间，通常用 Ve(j) 表示。

例如，图 1 中从 V1 到 V5 有两条路径，V1 作为源点开始后，a1 和 a2 同时开始活动，但由于 a1 和 a2活动的时间长度不同，最终 V1-V3-V5 的这条路径率先完成。
但是并不是说 V5 之后的活动就可以开始，而是需要等待 V1-V2-V5
这条路径也完成之后才能开始。所以对于 V5 来讲，Ve(5) = 7。

• Vl(j)：表示在不推迟整个工期的前提下，事件 Vk 允许的最晚发生时间。

例如，图 1 中，在得知整个工期完成的时间是 18 天的前提下，V7 最晚要在第 16 天的时候开始，因为 a10 活动至少需要 2天时间才能完成，如果在 V7 事件在推迟，就会拖延整个工期。
所以，对于 V7 来说，它的 Vl(7)=16。

• e(i)：表示活动 ai 的最早开始时间，如果活动 ai 是由弧 <Vk,Vj> 表示的，那么活动 ai 的最早开始的时间就等于时间 Vk 的最早发生时间，也就是说：e[i] = ve[k]。

e(i)很好理解，拿图 1 中 a4 来说，如果 a4 想要开始活动，那么首先前提就是 V2 事件开始。所以 e[4]=ve[2]。

• l(i)：表示活动 ai 的最晚开始时间，如果活动 ai 是由弧 <Vk,Vj> 表示，ai 的最晚开始时间的设定要保证 Vj的最晚发生时间不拖后。所以，l[i]=Vl[j]-len<Vk,Vj>。

• 在得知以上四种统计数据后，就可以直接求得 AOE网中关键路径上的所有的关键活动，方法是：对于所有的边来说，如果它的最早开始时间等于最晚开始时间，称这条边所代表的活动为关键活动。由关键活动构成的路径为关键路径。

• 求关键路径的具体过程

对图 1 中的 AOE 图求关键路径，首先完成 Ve(j)、Vl(j)、e(i)、l(i) 4 种统计信息的准备工作。

• Ve(j)，求出从源点到各顶点的最长路径长度为（长度最大的）：

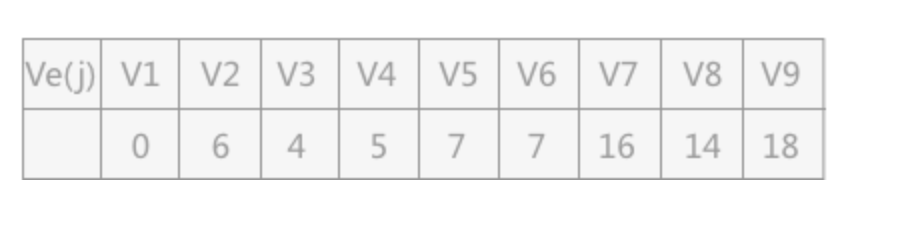
• Vl(j)，求出各顶点的最晚发生时间（从后往前推，多种情况下选择最小的）：
  

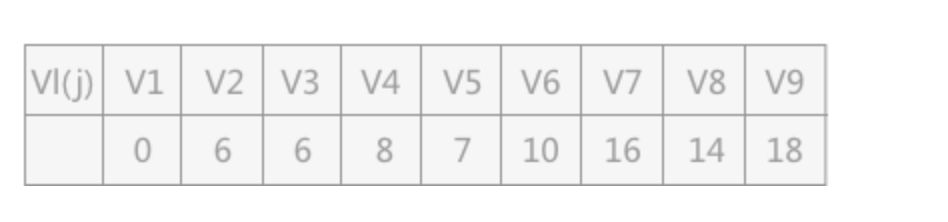
• e(i)，求出各边中ai活动的最早开始时间：
  

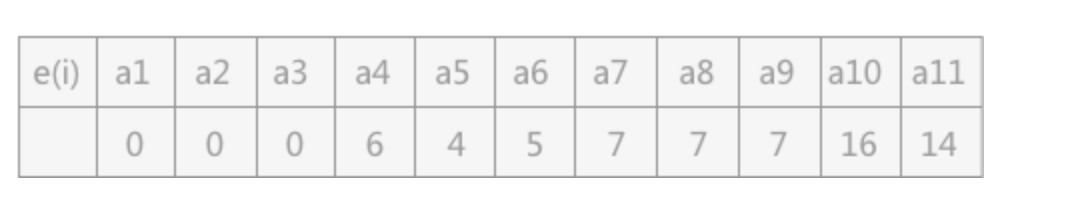
• l(i),求各边中ai活动的最晚开始时间（多种情况下，选择最小的）：
  
  通过对比 l(i) 和 e(i) ，其中 a1 、 a4 、 a7 、 a8 、 a10 、 a11 的值都各自相同，所以，在图 1 中的 AOE 网中有两条关键路径：
  

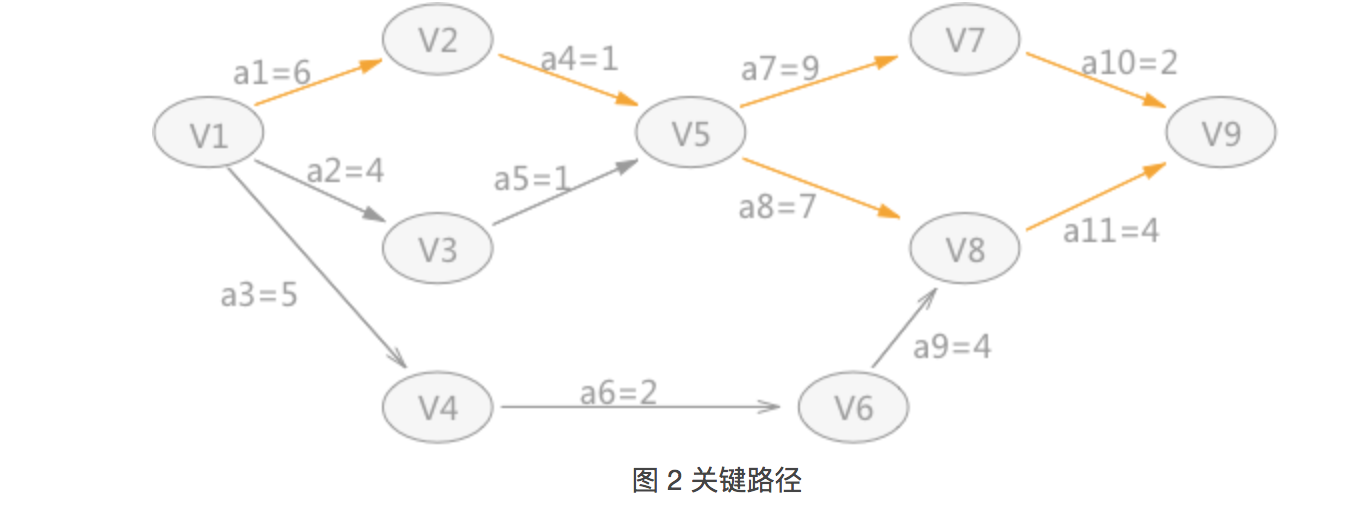
• 关键路径的代码实现

#include <stdio.h>
#include <stdlib.h>
#define
MAX_VERTEX_NUM 20//最大顶点个数
#define
VertexType int//顶点数据的类型
typedef enum{false,true} bool;
//建立全局变量，保存边的最早开始时间
VertexType ve[MAX_VERTEX_NUM];
//建立全局变量，保存边的最晚开始时间
VertexType vl[MAX_VERTEX_NUM];
typedef struct ArcNode{
int adjvex;//邻接点在数组中的位置下标
struct ArcNode * nextarc;//指向下一个邻接点的指针
VertexType dut;
}ArcNode;
typedef struct VNode{
VertexType data;//顶点的数据域
ArcNode * firstarc;//指向邻接点的指针
}VNode,AdjList[MAX_VERTEX_NUM];//存储各链表头结点的数组
typedef struct {
AdjList vertices;//图中顶点及各邻接点数组
int vexnum,arcnum;//记录图中顶点数和边或弧数
}ALGraph;
//找到顶点对应在邻接表数组中的位置下标
int LocateVex(ALGraph G,VertexType u){
for (int i=0; i<G.vexnum; i++) {
if (G.vertices[i].data==u) {
return i;
}
}
return -1;
}
//创建AOE网，构建邻接表
void CreateAOE(ALGraph **G){
*G=(ALGraph*)malloc(sizeof(ALGraph));
scanf("%d,%d",&((*G)->vexnum),&((*G)->arcnum));
for (int i=0; i<(*G)->vexnum; i++) {
scanf("%d",&((*G)->vertices[i].data));
(*G)->vertices[i].firstarc=NULL;
}
VertexType initial,end,dut;
for (int i=0; i<(*G)->arcnum; i++) {
scanf("%d,%d,%d",&initial,&end,&dut);
ArcNode *p=(ArcNode*)malloc(sizeof(ArcNode));
p->adjvex=LocateVex(*(*G), end);
p->nextarc=NULL;
p->dut=dut;
int locate=LocateVex(*(*G), initial);
p->nextarc=(*G)->vertices[locate].firstarc;
(*G)->vertices[locate].firstarc=p;
}
}
//结构体定义栈结构
typedef struct stack{
VertexType data;
struct stack * next;
}stack;
stack *T;
//初始化栈结构
void initStack(stack* *S){
(*S)=(stack*)malloc(sizeof(stack));
(*S)->next=NULL;
}
//判断栈是否为空
bool StackEmpty(stack S){
if (S.next==NULL) {
return true;
}
return false;
}
//进栈，以头插法将新结点插入到链表中
void push(stack *S,VertexType u){
stack *p=(stack*)malloc(sizeof(stack));
p->data=u;
p->next=NULL;
p->next=S->next;
S->next=p;
}
//弹栈函数，删除链表首元结点的同时，释放该空间，并将该结点中的数据域通过地址传值给变量i;
void pop(stack *S,VertexType *i){
stack *p=S->next;
*i=p->data;
S->next=S->next->next;
free(p);
}
//统计各顶点的入度
void FindInDegree(ALGraph G,int indegree[]){
//初始化数组，默认初始值全部为0
for (int i=0; i<G.vexnum; i++) {
indegree[i]=0;
}
//遍历邻接表，根据各链表中结点的数据域存储的各顶点位置下标，在indegree数组相应位置+1
for (int i=0; i<G.vexnum; i++) {
ArcNode *p=G.vertices[i].firstarc;
while (p) {
indegree[p->adjvex]++;
p=p->nextarc;
}
}
}
bool TopologicalOrder(ALGraph G){
int indegree[G.vexnum];//创建记录各顶点入度的数组
FindInDegree(G,indegree);//统计各顶点的入度
//建立栈结构，程序中使用的是链表
stack *S;
//初始化栈
initStack(&S);
for (int i=0; i<G.vexnum; i++) {
ve[i]=0;
}
//查找度为0的顶点，作为起始点
for (int i=0; i<G.vexnum; i++) {
if (!indegree[i]) {
push(S, i);
}
}
int count=0;
//栈为空为结束标志
while (!StackEmpty(*S)) {
int index;
//弹栈，并记录栈中保存的顶点所在邻接表数组中的位置
pop(S,&index);
//压栈，为求各边的最晚开始时间做准备
push(T, index);
++count;
//依次查找跟该顶点相链接的顶点，如果初始入度为1，当删除前一个顶点后，该顶点入度为0
for (ArcNode *p=G.vertices[index].firstarc; p ; p=p->nextarc) {
VertexType k=p->adjvex;
if (!(--indegree[k])) {
//顶点入度为0，入栈
push(S, k);
}
//如果边的源点的最长路径长度加上边的权值比汇点的最长路径长度还长，就覆盖ve数组中对应位置的值，最终结束时，ve数组中存储的就是各顶点的最长路径长度。
if (ve[index]+p->dut>ve[k]) {
ve[k]=ve[index]+p->dut;
}
}
}
//如果count值小于顶点数量，表明有向图有环
if (count<G.vexnum) {
printf("该图有回路");
return false;
}
return true;
}
//求各顶点的最晚发生时间并计算出各边的最早和最晚开始时间
void CriticalPath(ALGraph G){
if (!TopologicalOrder(G)) {
return ;
}
for (int i=0 ; i<G.vexnum ; i++) {
vl[i]=ve[G.vexnum-1];
}
int j,k;
while (!StackEmpty(*T)) {
pop(T, &j);
for (ArcNode* p=G.vertices[j].firstarc ; p ; p=p->nextarc) {
k=p->adjvex;
//构建Vl数组，在初始化时，Vl数组中每个单元都是18，如果每个边的汇点-边的权值比源点值小，就保存更小的。
if (vl[k]-p->dut<vl[j]) {
vl[j] = vl[k]-p->dut;
}
}
}
for (j = 0; j < G.vexnum; j++) {
for (ArcNode*p = G.vertices[j].firstarc; p ;p = p->nextarc) {
k = p->adjvex;
//求各边的最早开始时间e[i],等于ve数组中相应源点存储的值
int ee = ve[j];
//求各边的最晚开始时间l[i]，等于汇点在vl数组中存储的值减改边的权值
int el = vl[k]-p->dut;
//判断e[i]和l[i]是否相等，如果相等，该边就是关键活动，相应的用*标记；反之，边后边没标记
char tag = (ee==el)?'*':' ';
printf("%3d%3d%3d%3d%3d%2cn",j,k,p->dut,ee,el,tag);
}
}
}
int main(){
ALGraph *G;
CreateAOE(&G);//创建AOE网
initStack(&T);
TopologicalOrder(*G);
CriticalPath(*G);
return
0;
}

二、图的存储结构

1.图的顺序存储法

2.图的邻接表存储法

3.图的十字链表存储法

4.图的邻接多重表存储法

详情请点击：https://blog.csdn.net/wolfGuiDao/article/details/107587464

最后

以上就是喜悦小熊猫为你收集整理的数据结构--图(Graph)详解(一)数据结构–图(Graph)详解(一)的全部内容，希望文章能够帮你解决数据结构--图(Graph)详解(一)数据结构–图(Graph)详解(一)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。