Simulink 中连续与离散模型的区别

一、连续系统 VS 离散系统

1、定义

连续系统：系统状态的改变在时间上是连续的。
离散系统：系统状态的改变只发生在某些时间点上。

simpowersystem 的库中基本所有模型都属于连续系统，因为其对应的物理世界一般是电机、电源、电力电子器件等等，而simpowersystem 中常用 powergui 这个工具来将系统中的连续模型离散化以便采用 discrete 算法，便于计算机计算。

二、.连续模型的数学建模 vs 离散模型的数学建模

所谓数学建模就是用什么样的数学语言来描述模型。

连续系统的数学模型通常可以用以下几种形式表示：

1. 微分方程；
2. 传递函数；
3. 状态空间表达式；

. 这三种形式是可以相互转换的，其中又以状态空间表达式最有利于计算机计算

①微分方程

一个连续系统可以表示成高阶微分方程，即：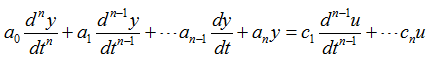

②传递函数

上式两边取拉普拉斯变换，假设 y 及 u 的各阶导数 (包括零阶 )的初值均为零，则有：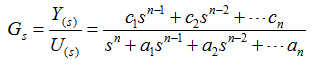

③状态空间表达式

线性定常系统的状态空间表达式包括下列两个矩阵方程：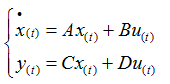

离散系统的数学模型通常有，1、差分方程 2、离散传递函数 3、权序列 4、离散状态空间模型等形式表示。

①差分方程的一般表示形式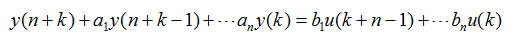

同样差分方程可以转换成后面那些表达形式。

三、.连续模型的离散化

为什么要将一个连续模型离散化呢？

主要是从系统的数学模型来考虑的， 前者是用微分方程来建模的， 而后者是用差分方程来建模的， 并且差分方程更适合计算机计算， 并且前者的仿真算法（simulationsolver ）用的是数值积分的方法，而后者则是采用差分方程的状态更新离散算法。

如何由一个连续模型得到它的离散模型，以及 powergui 是通过什么方法将连续模型离散化的，即
simulator 是如何将微分方程转换成差分方程的。

假设连续系统的状态方程为：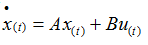

现在人为地在系统的输入及输出端加上采样开关，同时为了使输入信号复员为原来的信
号，在输入端还要加一个保持器，如图所示。 现假定它为零阶保持器， 即假定输入向量的所
有分量在任意两个依次相连的采样瞬时为常值， 比如， 对第 n 个采样周期 u(t)=u(nt) ， 其中 T
为采样间隔。

由采样定理可知，当采样频率 ws 和信号最大频率 wmax 满足 ws>2wmax 的条件时，可由
采样后的信号唯一地确定原始信号。 把采样后的离散信号通过一个低通滤波器， 即可实现信
号的重构。值得注意的是，图所示的采样器和保持器实际上是不存在的，而是为了将式离
散化而虚构的。

通过拉斯变换求解再反拉斯变换和卷积，就可以得到一个带有采样时间T的差分方程；只要涉及到离散就一定有采样时间。

四. simulator 连续模型的仿真算法（仿真解算器）和步长的概念。

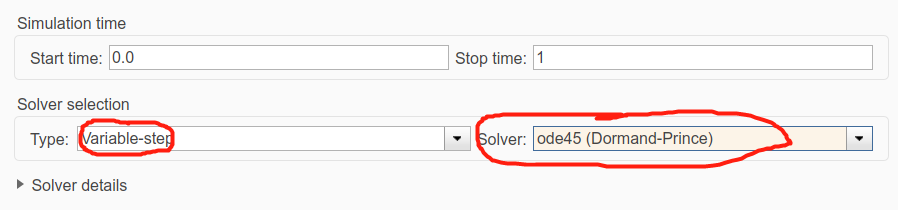
连续系统的计算机仿真算法是数值积分法， 即计算机用数值积分来解微分方程， 从而得到其
近似解。具体方法如下：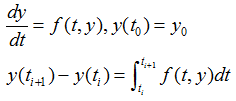

上式右端的积分是计算机无法求出的，其几何意义为曲线 f（t,y） 在区间 (ti ,ti+1) 上的面积。
当(ti ,ti+1) 充分小时，可用矩形面积来近似代替：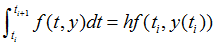

其中 h 即为积分步长。

当然求解连续系统的计算机仿真算法有好多种。

五、 simulator 离散模型的仿真算法和步长的概念。

离散模型的数学建模一般采用差分方程的方式， 在 matlab 中其仿真算法是采用 discrete 算法，就是根据 simulation step 定时对离散模块进行更新（就是定时计算差分方程的意思）。

至于其步长的概念和连续模型中 h 的概念差不多，但是它的大小选择和 sample time 有着密
切关系，下面会给予说明。

六、simulink 中仿真参数设置

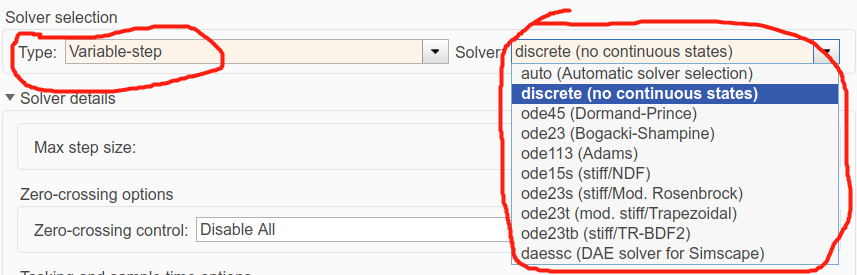
continuous solver 就是数值积分法， discrete solver 就是离散解法。（）

关于步长：

步长有 variable step（变步长）和 fixed step （固定步长之分） 。
continuous solver 中的步长就是 h，就是积分时间间隔。
对于 discrete solver 的步长是和要仿真的模型中的 sample time 有密切关系的，是不可以随便取的。
solver（ODE 表示常微分方法）

①variable step（变步长）

变步长会根据模型状态的变化的快慢适当调节步长，也就是相邻仿真计算的时间间隔，这样在保证了一定精度的同时又减少了仿真的次数，从而减小了仿真时间。对于 continuous solver 而言，可以人为设定 max step size 和 min step size ，然后计算机自动选择积分步长 h 进行数值积分。

②fixed step （固定步长）

仿真从头到尾用同一个步长。 Note： 对于 continuous solver 而言固定步长可以认为任
取；而对于 dicretesolver 而言固定步长可以 auto（即仿真帮你取） ，若人为取必选要遵守和
sample time 之间的一定关系，下面会有介绍。

③discretesolver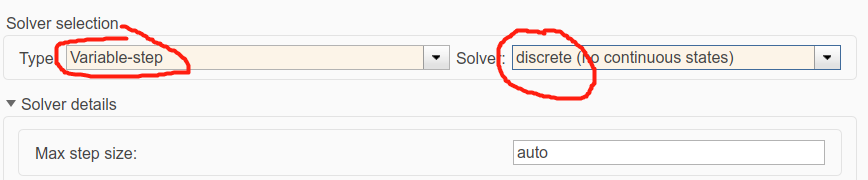


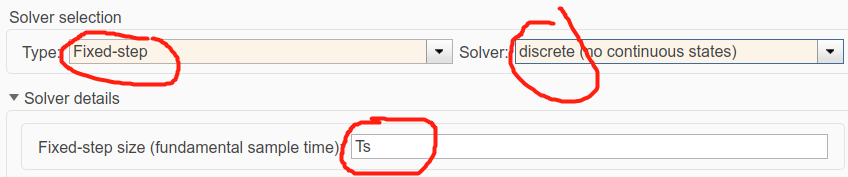
solver就是 discrete 算法，就是不断更新 discrete block 在各离散点的状态，步长的大小是与模型中的 sampletime 有密切关系的，由上面阐述的差分方程可知，差分方程中 T 采样时间是固定的，对discrete solver 而言不管是 variable step 还是 fixed step， simulation step （仿真步）必须要有出现在 sample time 所有的整数倍上，即 simulation step 的设置必须使 simulator 在 1T、 2T、 3T 要对模型进行计算
仿真，以免错过主要状态的转化。

若一个离散仿真模型中具有多个 sample time，那么要保证每个模型在其采用时间的 1T、
2T、 3T 都能进行仿真，那么最小步长只能取各个仿真时间的公约数，其中最大公约数又称
为 fundamental sample time，例子如下
假设仿真的离散模型中有两个采样时间 T1=2e-6 ， T2=4e-6 那么其公约数为 1e-6 和 2e-6，而
fundamental sample time=2e-6。

若采用 variable step 步长， simulator 会根据模型中的各个 sample time 自动调整步长， 以使得
仿真时间时刻等于 sample time。

④关于 powergui 的作用

simulink仿真用到simpowersystom（模拟系统）库时，一般都要加powergui模块，它储存了电路模型的等效数学模型（状态空间方程），有三种运行模式：连续方法（continous）、离散方法（discrete）、相量方法（phasor）。

powergui 基本上在 simpowersystem 的仿真中有两个作用：

作用一：离散化系统中的一些连续（模拟）模型，以便 simulator 采用 discrete 算法计算。

注意：对本来就已经存在的离散模型不起任何作用，其设置的采样时间只对仿真中的模拟系统部分起作用，如果设置了固定步长值，其采样时间也要是固定步长的整数倍。

作用二：提供各种 graphical userinterface tools 用于分析仿真过程中的信号以及数据 （尤其是 FFT
分析）

最后

以上就是老迟到手机为你收集整理的Simulink 中连续与离散模型的区别的全部内容，希望文章能够帮你解决Simulink 中连续与离散模型的区别所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。