文章目录:
- 2.1 图像增强概述
- 2.2 灰度变换函数
- 2.2.1 幂律变换
- 2.2.2 分段线性变换
- 2.2.3 图像处理工具箱(IPT)中的函数imadjust
- 2.2.4 对数变换
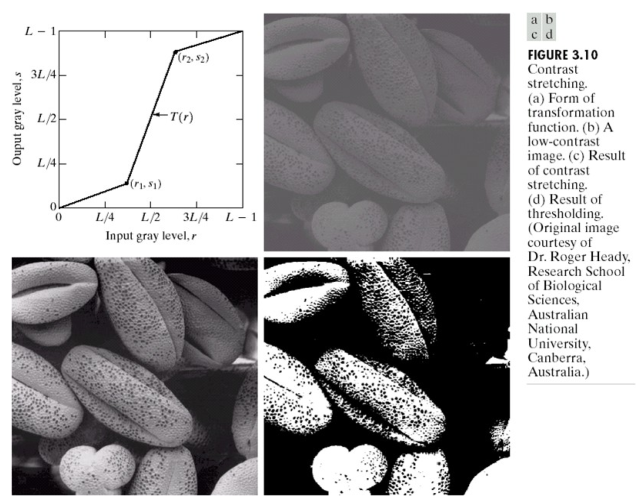
- 2.2.5 对比拉伸变换
- 2.3 直方图处理
- 2.3.1 图像直方图(统计图像灰度级分布)
- 2.3.2 直方图均衡
- 2.3.3 直方图匹配(利用直方图均衡进行搭桥)
2.1 图像增强概述
1)增强的主要目的是对图像进行处理,使结果图像比原图像更适合于某一 特定应用。 特定意味着技术是非常面向问题的。
2)图像增强方法可分为两大类: 空域方法和频域方法。
(1)空域方法是基于图像中的像素的直接进行局部处理。
(3)频域技术是基于图像的傅里叶变换进行处理。
3)目前还没有图像增强的一般理论
(1)当一幅图像增强效果通过人的视觉进行评估时,观察者是一个特定方法工作好坏的最终判断者,这使得比较不同方法的性能变得困难。
(2)若采用机器感知评判时,评价任务相对简单一些,如字符识别任务。
4) 空间域处理的数学表示:
g(x,y) = T[f(x, y)]
(1)其中 f (x, y): 输入图像
(2)g(x, y): 输出图像
(3)T : 在 f (x, y) 上 的 操 作 ,定义在 (x, y) 的某个邻域上,T 可以在一组图像上进行操作, 例如噪声消除,方形和矩形邻域是使用最多的,因为它们易实现, 也可使用圆形区域。T 最简单的情况是邻域大小为1×1。这时 g 只依赖于 f 在 (x, y) 处的值,即
s = T (r)
我们称之为灰度变换或亮度变换,其中 s 与 r 分别为输出与输入的亮度值。
2.2 灰度变换函数
2.2.1 幂律变换
1)幂律变换表达式:
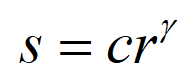
其中c、 γ为正常数
2)幂律变换图像:
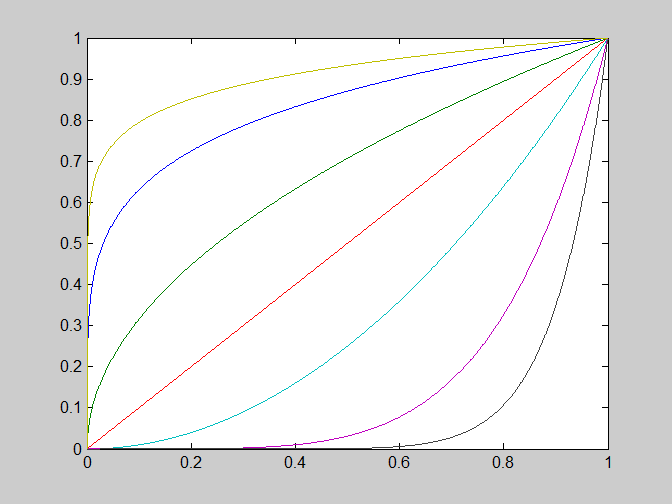
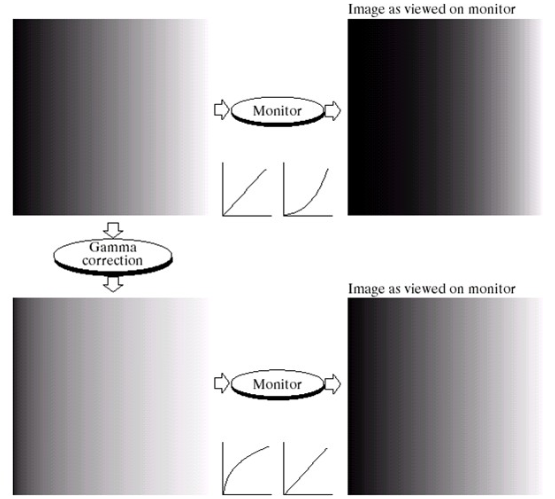
2)应用例子1:伽马校正
显示器在显示真实图像时,往往灰度值不是一一对应的,一般情况都对应一个伽马曲线,为了使显示灰度和真实灰度相同,需要一个校正函数将灰度先变换一下
3)应用例子2 :对比度增强
(1)γ<1(暗变亮)
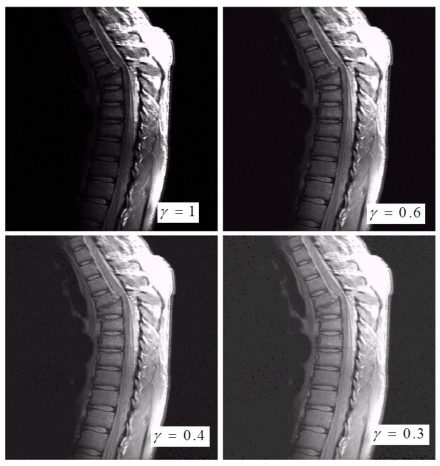
(2)γ>1(亮变暗)

2.2.2 分段线性变换
1)其变换函数为不同线性函数组合
2)应用举例1:将特定灰度值范围进行对比度拉伸
3)应用举例2:灰度切割将特定灰度范围设置为某一特定灰度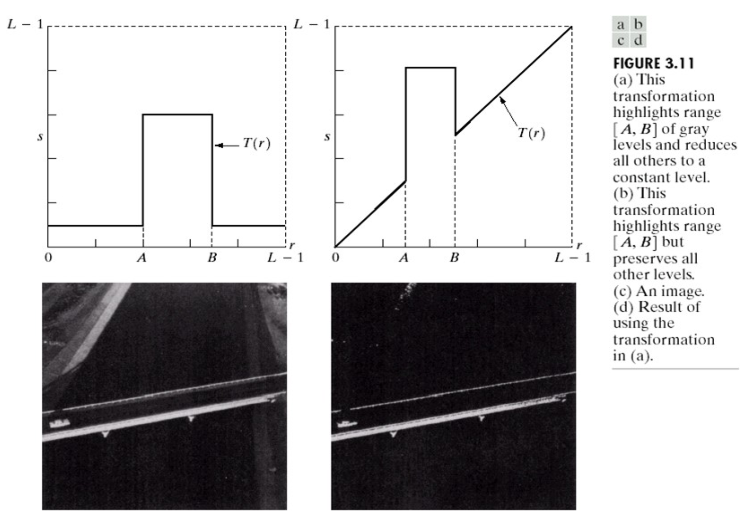
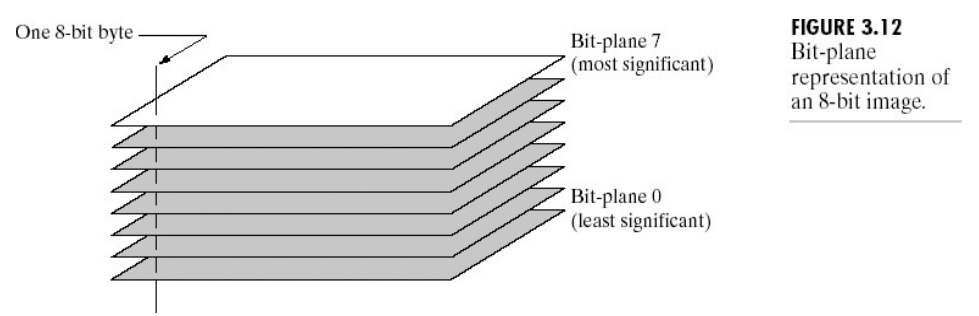
4)应用例子3: 比特位面图像将图像中的每个像素由8位二进制数表示转化为图像由8个1位平面组成,最小有效位平面为0位平面,最大有效位平面为7位平面。

2.2.3 图像处理工具箱(IPT)中的函数imadjust
1)imadjust介绍
(1)g=imadjust(f, [low_in, high_in],[low_out,high_out],gamma)
(2)这个函数将图像f中的强度值映射到g中的新强度值.
(3)使low_in和high_in之间的值映射到 low out和high out之间的值。
(4)比low_in还低的和比high_in还高的将会被裁减;就是说比low_in还低的值对应到low_out,比high_in还高的值映射到high_out.
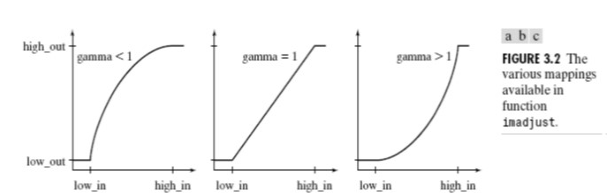
(5)参数 gamma 指定了将 f 中强度值映射成 g 中强度值的映射曲线的形状
(6)如果 gamma 小于 1 ,该映射倾向于产生更高的亮度输出值,如左侧图所示。
(7) 如果 gamma 大于 1 ,该映射倾向于产生更低的的亮度输出值,如右侧侧图所示。
(8)如果函数参数中省略了它,默认为 gamma =1 的线性映射
2)应用举例
(1)灰度反转:左图为f,右图为g
f = imread(‘...’);
g = imadjust(f,[0 1],[1 0]);
subplot(1,2,1);imshow(f); subplot(1,2,2);imshow(g);

(2)灰度变换
h = imadjust(f,[0.5 0.75],[0 1]);
i = imadjust(f,[],[],2);
subplot(2,2,1);imshow(f);
subplot(2,2,2);imshow(g);
subplot(2,2,1);imshow(h);
subplot(2,2,2);imshow(i);

2.2.4 对数变换
1)对数变换和对比拉伸变换是动态范围处理的基本工具。
2)对数变换是用这个数学表达式实现的:
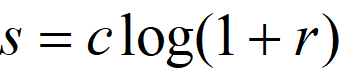
(1)其中 c 是常数 .
(2)该变换的形状类似于 gamma 曲线。
(3)请注意,伽马曲线的形状是 可变的,而对数函数的形状是 固定的。
(4)+1的目的是防止灰度变为无穷
3)对数变换的主要用途之一是压缩动态范围
(1)例如,傅里叶谱(第4章)的值在[0,10 6 ]或更高的范围内并不少见。当显示在一个线性缩放到8位的显示器上时,高值占据了显示器的主导地位,从而丢失了低强度值的视觉细节频谱。通过计算log,动态范围例如10 6 减少到大约14,这更易于显示管理。
(2)执行对数转换时,通常希望将压缩后的值恢复到显示的全部范围。对于8位,在MATLAB中最简单的方法是使用这个语句
gs= im2uint8(mat2gray(g));
使用 mat2gray 将值映射到[0,1]范围,而 im2uint8 将值映射到[0,255]范围。
3)应用举例:
g = im2uint8(mat2gray(log(1 + double(f))));
imshow(g)

2.2.5 对比拉伸变换
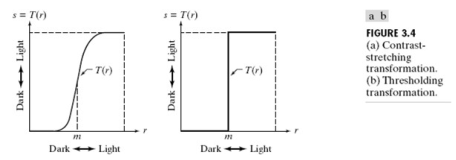
1)一个对比拉伸变换函数可以定义为:
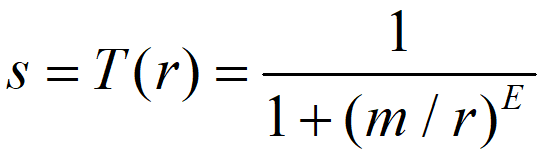
(1)它将小于 m 的输入值压缩到输出图像中较窄的暗区范围内;
(2)类似地,它将 m 以上的值压缩成输出中的窄带亮区;
(3)其中 r 为输入图像的强度, s 为输出图像中对应的强度值,E控制函数斜率, m 为参数。
(4)在MATLAB中,可以用下面这个表达式处理整幅图像
g= 1./(1 + (m./(double(f) + eps)).ˆE)
2.3 直方图处理
2.3.1 图像直方图(统计图像灰度级分布)
1)亮度变换通常是基于从图像亮度直方图中提取的信息进行的,直方图在在很多图像处理方面(图像增强、压缩、分割和描述)都起到基础的作用。
2)一幅亮度取值在[0,G]范围的数字图像,将它量化为L个亮度级别的直方图可以定义为一个离散函数:
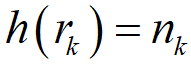
其中r k 为区间[0,G]中的第k个强度级别类,n k 为图像中强度级别为r k 的像素数目。uint8类图像的G值为255,uint16类图像的G值为65535,double类图像的G值为1.0。
3)一幅图像的直方图h(r k )可以表示为一个向量,将其所有分量除以该图像的像素总数,可得到对应的归一化直方图,即
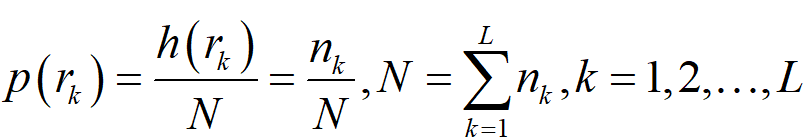
从基本概率论知识可知, p(r k ) 可看作为在一幅图像中强度级 r k 发生概率的估计值。
4)Matlab中图像直方图函数
h=imhist(f,b)
(1)其中 f 为输入图像, h 为输入图像的直方图, b 为生成直方图所用量化级别的数目。
如参数中不包含 b ,则默认使用 b = 256。量化级别是对亮度范围的一种子划分。
(2)例子
f=imread(’timg.jpg’);
%返回的是一个包含各个级别个数的数组
imhist(f)
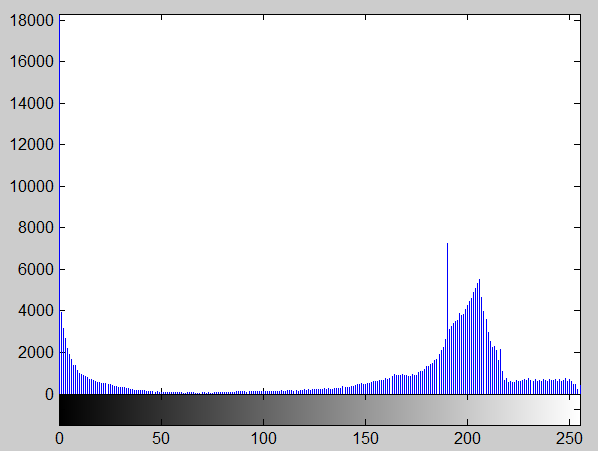
%计算归一化直方图
p=imhist(f,b)/numel(f)
5)用bar绘制图像直方图
我们通常用柱状图绘制直方图,可使用matlab函数bar(horz,v,width)实现。
(1)其中v是一个行向量,包含要绘制的点的纵坐标。
(2)horz是一个维数与v相同的向量,它包含水平尺度的增量。如省略了horz,则水平轴的单位是从0到长度v的长度。
(3)宽度是介于0和1之间的一个数。
(4)例子:
f=imread(’timg.jpg’);
h1=imhist(s,16);
horz=1:16;
bar(horz,h1,0.8)
axis([0 16 0 65000]);
set(gca,’xtick’,0:1:16);
set(gca,’ytick’,0:4000:65000);
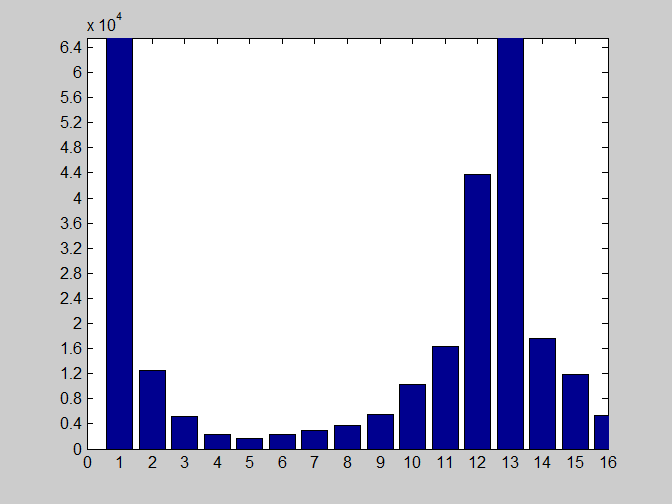
6)用stem绘制图像直方图
(1)函数stem类似于bar。语法是:
stem(horz, v, ’color linestyle marker’, ’fill’)
(2)其中 v,horz 与 bar 中的参数描述相同。
(3)Color_linestyle_marker 是下表中值的三元组 。
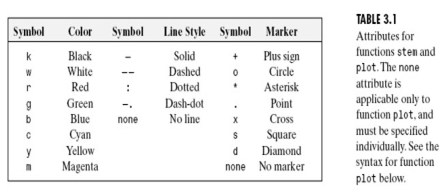
(4)使用stem绘制直方图例子
stem(v, ’rs’)
• 生成一个线段图,其中线和标记是红色的,线是虚线,标记是正方形。
• 如果指定‘fill’,且使用的标记是圆形、正方形或菱形,则标记用指定的颜色填充。
• 默认的颜色为黑色,默认的线型为实线,默认的标记为圆形
hi = imhist(f,32);
stem(hi,'r-s','fill');
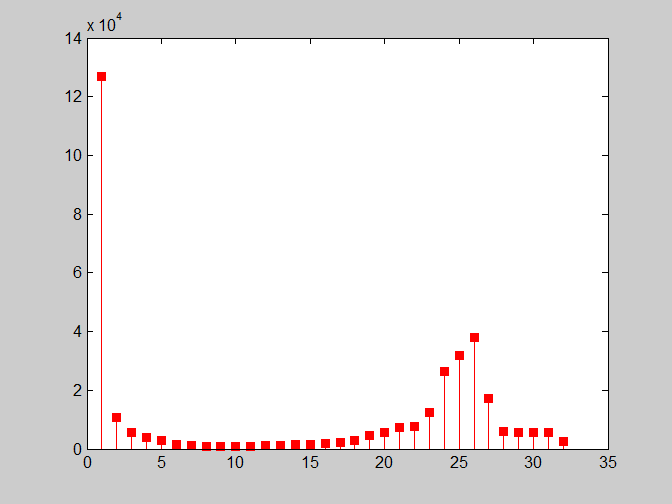
7)用plot绘制图像直方图
(1)函数plot是用直线连接一组点。语法是:
plot(horz, v, ’color_ linestyle_marker’);
(2)其中参数如前面stem函数的定义相同。.
(3)函数plot是常用来绘制函数图像,而且可以将多组函数绘制在一个坐标系下。
(4)示例:
hi=imhist(s,32);
plot(hi);
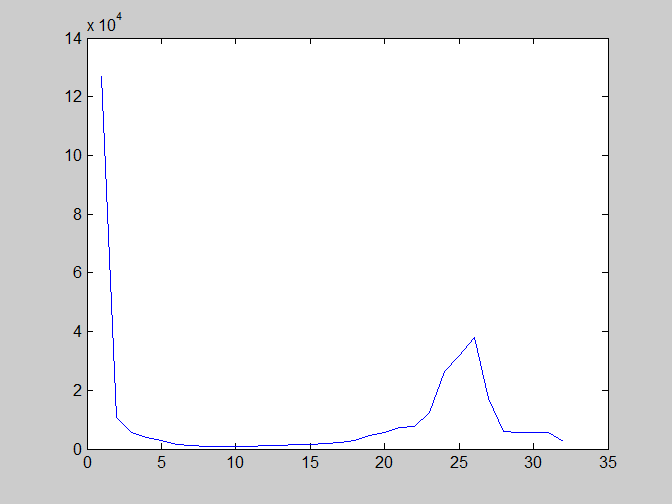
2.3.2 直方图均衡
• 目的:改善图像的对比度。
• 结果:均衡后的的图像具有 几乎均匀的像素值分布。
• 优点: 无参数的算法
1)直方图均衡离散表达式
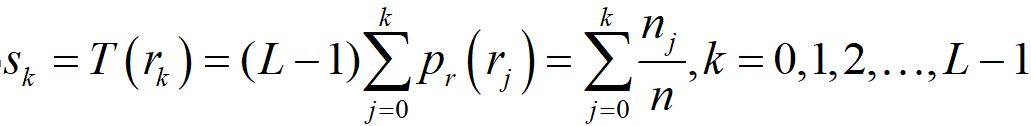
利用该映射,可将将输入图像中 r k 级的每个像素映射到 s k 级对应的像素,从而得到均衡后输出图像
2)直方图均衡化是通过函数histeq在工具箱中实现的,函数的语法如下:
g = histeq(f, nlev)
(1)其中 f 为输入图像, g 为均衡后的输出图像,nlev为输出图像指定的亮度级别数。
(2)如果nlev等于L (输入图像中亮度级总数),那么histeq直接实现转换函数。如果nlev小于 L ,那么histeq将尝试分布这些级别使它们近似于一个平坦的直方图。
3)直方图均衡举例:
f = imread('timg.jpg');
subplot(2,2,1);imshow(f);
subplot(2,2,2);imhist(f);
g = histeq(f,256);
subplot(2,2,3);imshow(g);
subplot(2,2,4);imhist(g);
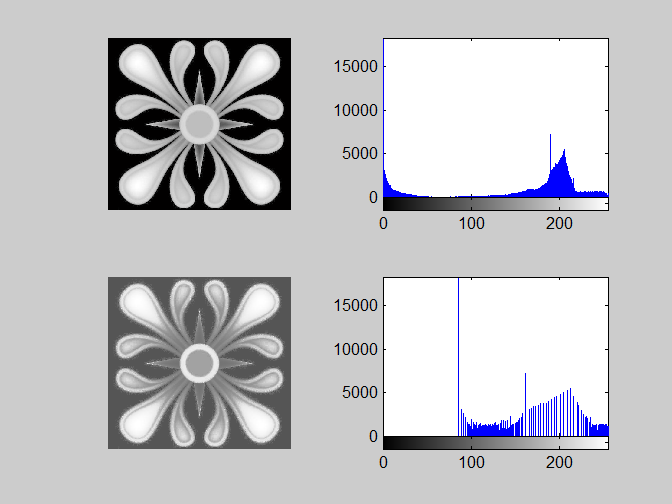
4)直方图均衡还不够完美!有的时候无法达到图像增强的目的,来看一个失败的例子:
f = imread('mood.tif');
g = histeq(f,256);
subplot(1,2,1);imshow(f);
subplot(1,2,2);imshow(g)

2.3.3 直方图匹配(利用直方图均衡进行搭桥)
1)直方图匹配类似于直方图均衡化,只不过我们不希望输出图像具有扁平的直方图,而是希望输出图像的直方图具有指定的形状。
2)考虑一下标准化到区间[0,1]的连续亮度级,令 r 和 z 分别表示输入和输出图像的亮度级。输入图像的亮度分布服从概率密度函数 p r (r),输处图像的亮度分布服从指定的概率密度函数 p z (z)
3)变换后的直方图具有相同的直方图均衡,利用直方图均衡进行搭桥即可求出变换函数
4)利用直方图匹配解决前面的图像
(1)本例中直方图均衡化的问题主要由于原始图像中像素的高度集中在0附近,因此一种合理的方法是修改该图像的直方图,使其不具有此属性。
(2)解决这种情况的一种可能方法就是使用直方图匹配。我们希望输出图像保持原始图像的直方图的一般形状,同时将源图像在灰度级低端的密集情况进行改善,使其变得分布更广泛、分散。
(3)我们注意到原始图像的直方图基本上是双峰的,一个大的模式在原点,另一个小的模式在灰度的高端。例如,可以使用多模态高斯函数对目标直方图进行建模。
(4)我们用下面的函数twomodegauss计算一个归一化到单位面积的双峰高斯函数,用它可以作为一个指定的直方图。下面的交互函数接受键盘输入,并绘制得到的高斯函数。
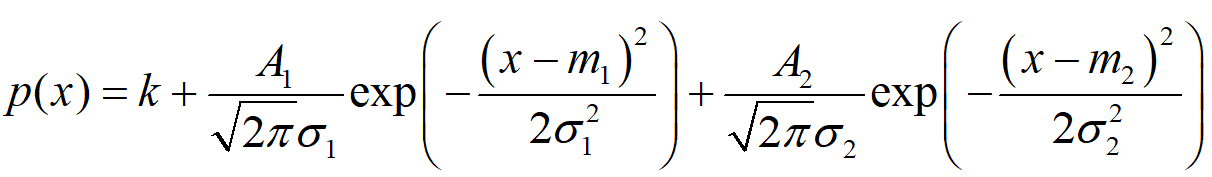
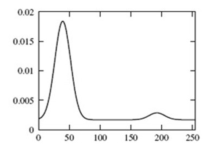
(5)示例程序:
g = histeq(f,p);
其中p为上面式子的七个常数,顺序为m1, sig1, m2, sig2, A1, A2, k
f = imread('mood.tif');
g = histeq(f,256);
subplot(2,3,1);imshow(f);
subplot(2,3,4);imhist(f);
subplot(2,3,2);imshow(g);
subplot(2,3,5);imhist(g);
q = [30 8 180 100 6 1 20]
h = histeq(f,q);
subplot(2,3,3);imshow(h);
subplot(2,3,6);imhist(h);
可以获得较好的效果:
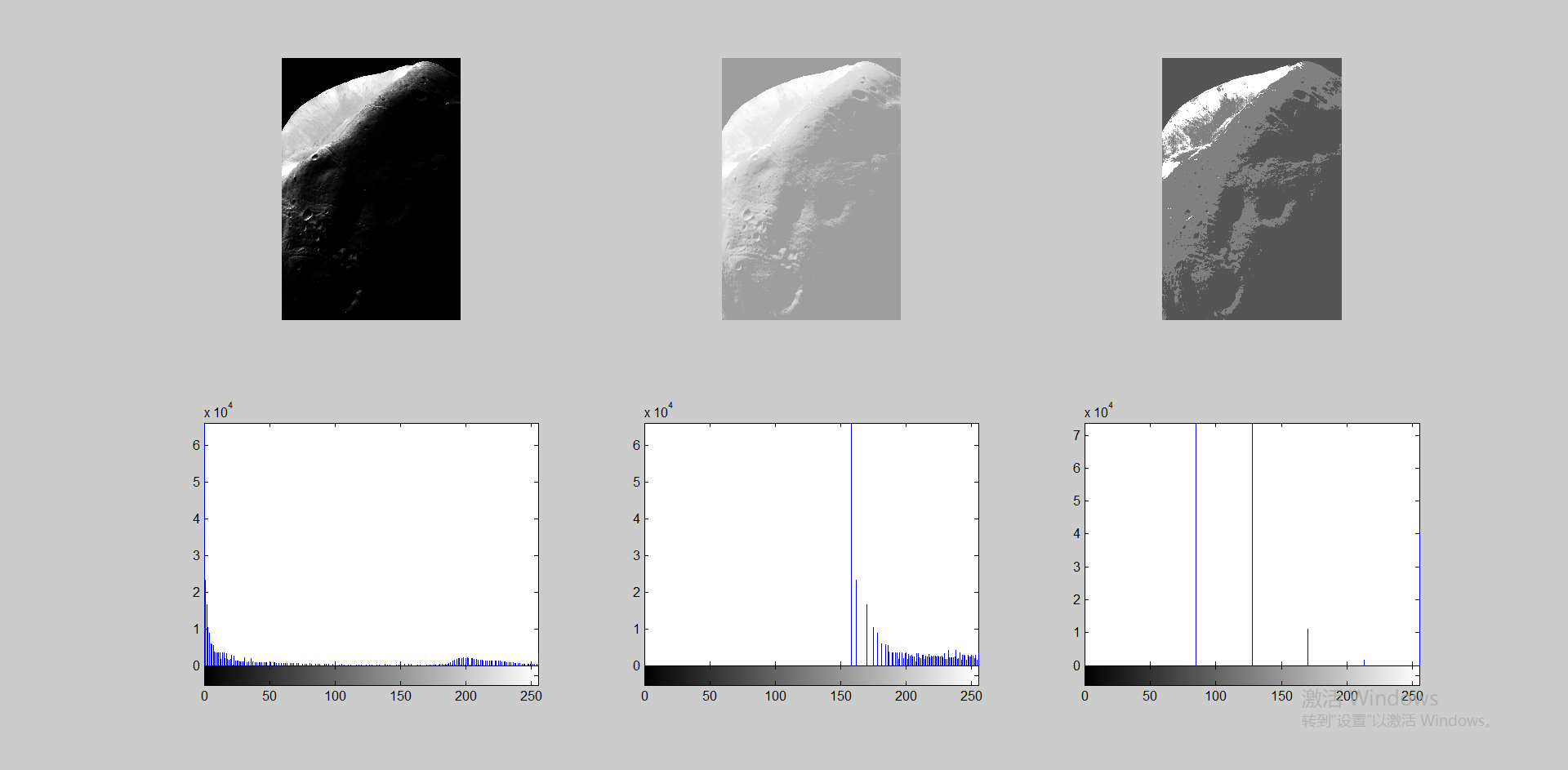
最后
以上就是故意草莓最近收集整理的关于2. 空域处理(上)2.1 图像增强概述2.2 灰度变换函数2.3 直方图处理的全部内容,更多相关2.内容请搜索靠谱客的其他文章。








发表评论 取消回复